가능도(Likelihood)

특정 사건이 일어날 가능성을 비교하는 방법

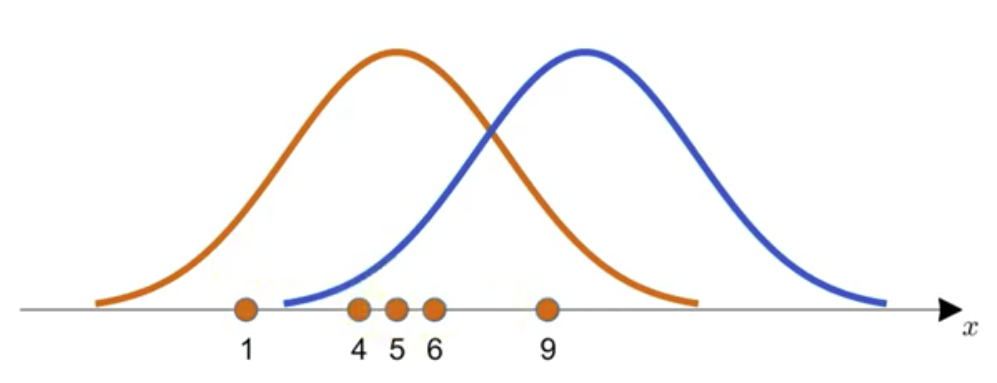
위와같은 확률밀도함수 2개중 하나로부터 관측값 $x=[1, 4, 5, 6, 9]$ 라는 데이터를 얻었다면 어떤 분포로부터 해당 데이터가 추출 되었을지

생각해보면 주황색에서 얻었을 확률이 더 높다 생각할 수 있다.(데이터의 중심과 가깝기 때문)

수식으로 서술하면 아래와 같다.
\(\mathrm{Likelihood\ Function}= P(x|\theta) = \prod^n_{k=1}P(x_k|\theta)\)

그림처럼 주어진 데이터의 PDF 값을 다 곱해준값을 Likelihood 값이라 한다.

최대 우도 추정법 (MLE: Maximum Likelihood Estimation)

Likelihood Function 이 최대값이 될 수 있는 정규분포의 $\theta$(평균값) 를 계산하는 것

편하게 계산하기 위해 Log Likelihood Function 을 사용하는데 기존 수식에 로그를 취해주면 아래와 같이 변환되기 때문

\[\begin{aligned} L(\theta|x) &= \log P(x|\theta) \\ &= \log\prod^n_{k=1}P(x_k|\theta) \\ &= \sum^n_{k=1}\log P(x_k|\theta) \end{aligned}\]

$L(\theta

x)$ 를 $\theta$ 에 대한 편미분을 통해 Likelihood Function의 최대값을 알 수 있다.