큰수의 법칙(law of large numbers) - 기대값과 평균
큰 수의 법칙 은 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다는 개념이다.
주사위를 $n$번 굴력 나온 평균을 출력해보면 1~6 의 평균인 $3.5$ 정도의 전후의 값이 나올것이다.
$n$ 값이 커질수로 주사위눈 평균값인 3.5에 가까워지는것을 직관적으로 알 수 있는데
큰수의 법치에 기반된 직관이라 할 수 있다.
iid의 대표적인 예인 주사위 확률을 기반으로 큰수의 법칙을 생각해보자.
iid(독립 동일 분포: independent and identically distributed) 1부터 20까지의 주사위눈을 $X_1$ 부터 $X_{20}$ 으로 설정할때
각 확률변수 $X_n$ 에서 어떤 숫자가 나올 확률은 모두 같을것이다.
$P(X_1=1) = P(X_2=2) = P(X_n=4) = \frac{1}{6}$ 첫번째 나온 결과과 두번째 나온 결과에 영향을 끼치지 않는 독립이고 매순간의 확률변수가 동일한 경우 독립 동일 분포(이하 iid) 라 부른다.
각 $w$ 의 평균 $_n$ 를 구하고 모든세계의 $X_1, X_2, …, X_n$ 를 모아 기대값과 분산을 출력해보자.
$Z_n = \frac{X_1 + X_2 + \cdots + X_n}{n}$
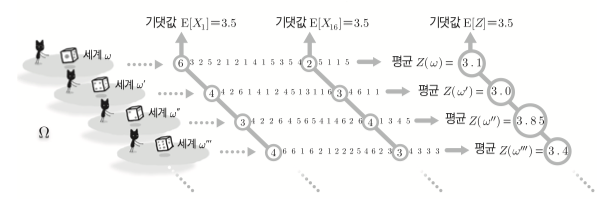
$E[Z_n] = E[\frac{X_1+X_2+…+X_n}{n}] = \frac{E[X_1+X_2+…+X_n]}{n} = \frac{E[X_1]+E[X_2]+…+E[X_n]}{n} = \frac{nm}{n} = m$
$V[Z_n] = V[\frac{X_1+X_2+…+X_n}{n}] = \frac{V[X_1+X_2+…+X_n]}{n^2} = \frac{V[X_1]+V[X_2]+…+V[X_n]}{n} = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}$
iid 이기에 에서 각 $X_1, X_2, …, X_n$ 의 기대값은 $m$, 과 분산은 $\sigma^2$ 로 치환할 수 있기 때문에 위와같은 식이 성립한다.
$V[Z_n]$ 의 경우 원래 분산에서 $\frac{1}{n}$ 배가 되었는데 $w$ 세계의 각 평균값에 대하여 분산처리 한 것이기 때문에 당연히 기존 분산값 $\sigma^2$ 보다 작아질 수 밖에 없다.
만약 $n \rarr \infty$ 이라면 $V[Z]$ 는 0에 가까워질 것이다.
분산 0 은 오차가 없어진다는 뜻, 각 $Z_n \to m$ 에 수렴한다는 뜻이다.
이런 현상을 큰수의 법칙 이라고 하며 수식으로 표현하면 아래와 같다.
| $\lim_{n \to \infty}P( | \frac{X}{n} - p | < \epsilon ) =1 $ |
$n$ - 시행 횟수
$X$ - 시행 횟수중 해당 사건이 일어난 횟수
$p$ - 수학적 확률, 주사위의 경우 $\frac{1}{6}$ 이다.
$\epsilon$ 은 0에 가까운 매우 작은 양수
| $ \lim_{n \to \infty}P( | \bar{X_n} - m | < \epsilon ) =1 $ |
$\bar{X_n} = \frac{1}{n}\sum_k^nX_k$
통계적 확률 $\frac{X}{n}$ 과 수학적 확률 $p$ 가 $n$ 이 커질수록 근사해진다는 이론이다.
중심극한정리
현실의 여러 확률값은 중심값이 나오기 쉽고, 중심값 부근이 나올 확률이 많고, 그외의 값들은 나오기 어렵다
수십개의 표본에 대하여 위의 표본평균을 그래프로 만들면 정규분포 형태로 나온다는 것이 중심극한정리
예로 대한민국 성인 남자 키를 중심극한정리로 표현한다면
10명씩 총 10만개의 표본을 만들고 해당 표본의 평균을 구하면 175cm 를 정점으로 하는 정규분포가 출력된다는 뜻
현실의 여러 통계들이 정규분포로 간주되는 경우가 많다.
iid 에서 환경 $X1 + … + X_n$ 개의 표본이 있을 때
분산 $V[X]$ 에 대해 생각해 보면 무작위로 뽑은 표본의 동요 라 할 수 있다.
$W_n = \frac{X_1 + … + X_n}{\sqrt{\sigma}}$
그리고 이 동요의 축적 $V[X1 + … + X_n]$ 는 n 개의 세상의 모든 분산값들을 더한값이기에 $n\sigma^2$ 로 발산한다.