연속확률분포 - 정규분포

정규분포: (Normal distribution)

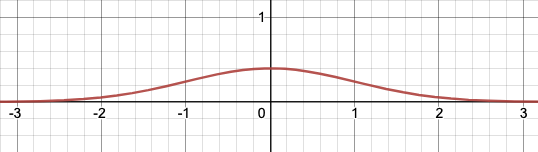
위 주사위 이항분포 예제의 $n$ 을 실셈이 불가능할만큼 계속 늘리면서 그래프를 구하면 아래와 같은 그래프가 나오는데

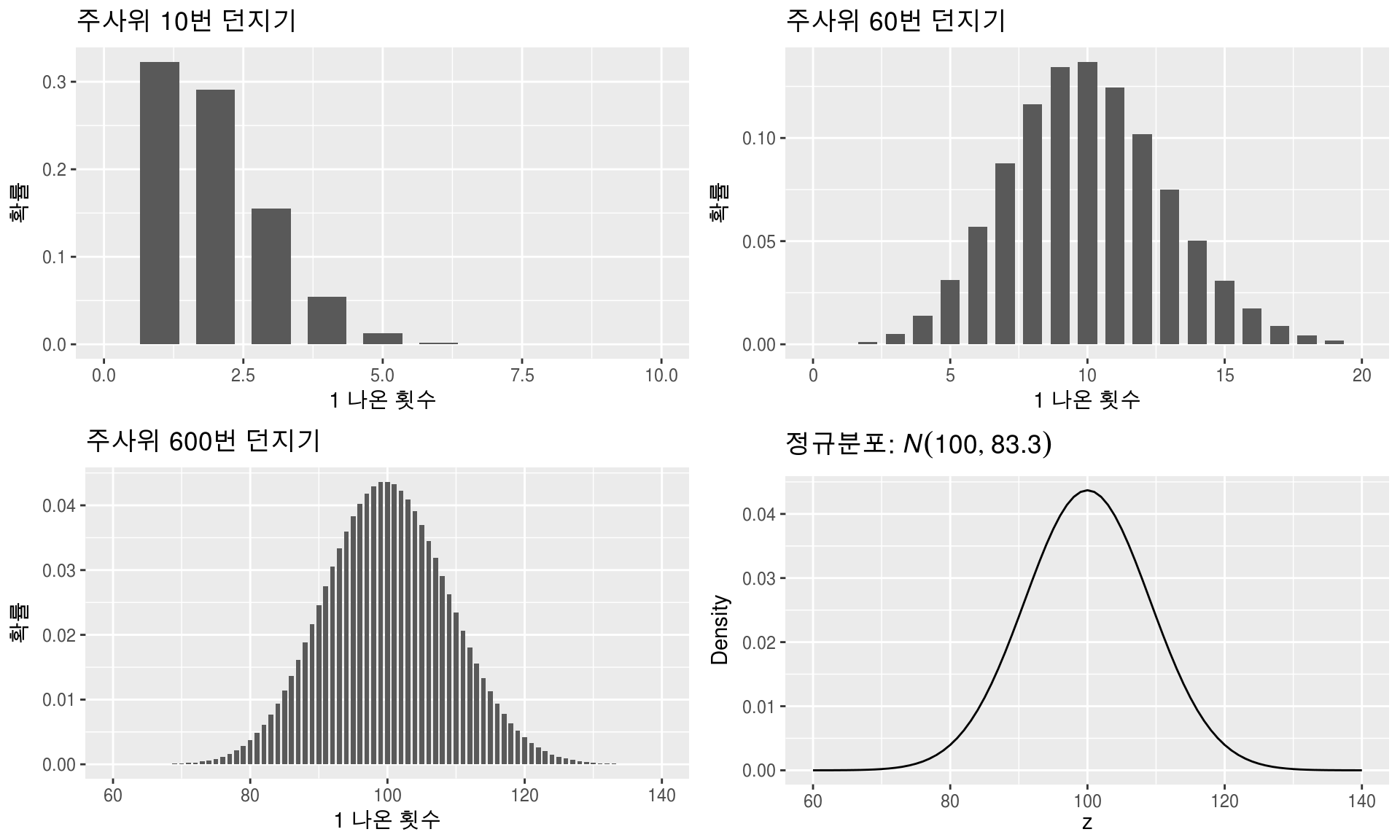
저런구조를 가진것을 정규분포 라 한다.

그리고 정규분포를 PDF 로 표현하면 아래와 같다.

\[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-m)^2}{2\sigma^2}}\]

정규분포식 으로 아래와 같이 표기한다. \(X \sim N(m, \sigma^2)\)

평균 $m$ 과 분산 $\sigma$ 만 알 수 있다면 정규분포 그래프를 그릴 수 있다.

확률밀도함수를 살펴보면 다음과 같은 특징이 있다.
$m, \sigma$ 값 관계 없이 $3\sigma$ 안에 면적의 99.73% 를 차지한다.

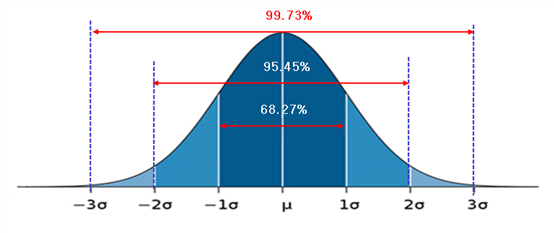
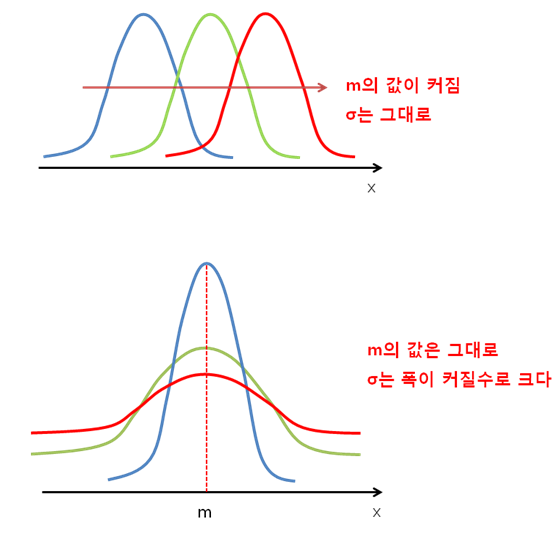
표준정규분포

정규분포를 표준화한 분포

표준화란 주어진 변량 $X$ 를 아래 $Z$로 변화시키는 과정이다. $X \rarr Z$

\[Z = {X-m \over \sigma}\]

이 과정을 거치면 $m=0, \sigma=1$ 이 된다.

\[E(Z) = E({X-m \over \sigma}) = E(\frac{1}{\sigma}X - \frac{m}{\sigma}) = \frac{1}{\sigma}E(X) - \frac{m}{\sigma} \\ \ \\ \begin{aligned} &\because E(X) = m \\ \ \\ &\therefore \frac{1}{\sigma}E(X) - \frac{m}{\sigma} = \frac{m}{\sigma} - \frac{m}{\sigma} = 0 \\ \ \\ &\therefore E(Z) = 0 \end{aligned}\] \[V(Z) = V({X-m \over \sigma}) = V(\frac{1}{\sigma}X - \frac{m}{\sigma}) = \frac{1}{\sigma^2}V(X) \\ \ \\ \begin{aligned} &\because V(X) = \sigma^2 \\ \ \\ &\therefore \frac{1}{\sigma^2}V(X) = \frac{1}{\sigma^2}\sigma^2 = 1 \\ \ \\ &\therefore V(Z) = 1 \end{aligned}\]

모든 표준화를 거친 정규분포는 아래 정규분포식 으로 표기될 수 있다.

\[Z \sim N(0, 1)\]

$m = 0, \sigma = 1$ 로 변했기 때문에 PDF도 아래처럼 변한다.

\[f(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^{2}}{2}}\]

확률밀도함수는 아래와 같다.

이산확률분포 - 이항분포

이항분포: (二項分布: binomial distribution)

각 시행이 확률 p를 가질 때의 이산 확률 분포

확률 p 로 앞면이 나오는 동전을 n 번 던질때 앞면이 몇번 나올지 를 예로 들 수 있다.

수식은 아래와 같다.
$P(X=k) = _nC_k p^k q^{n-k}$

이항분포 와 조합을 기호로 표기할 수 있다.
$X \sim \mathrm{Bn}(n,p) =\begin{pmatrix}n\x\end{pmatrix}p^xq^{n-k}$

연속확률분포 - 균등분포

동전이나 주사위처럼 생길수 있는 확률이 $n$ 이고 모든 확률이 $\frac{1}{n}$ 인 분포를 균등분포라 한다.