공분산 (covariance)

분산이 하나의 확률 변수만을 위한다면 공분산은 두 개의 확률 변수의 선형관계를 나타내는 값이다.

두개의 확률변수 $X, Y$ 의 공분산 $\mathrm{Cov}[X,Y]$ 에 알아보자.

$X$ 와 $Y$ 의 기대값이 각각 $m, v$ 일 때 공분산 식은 아래와 같다.

\[\mathrm{Cov}[X,Y] = E[(X-m)(Y-v)] \\ = \frac{1}{n-1}\sum^n_{i=1}(x_i - m)(y_i - v)\]

두 변수의 확률밀도함수를 그림으로 나타내었는데

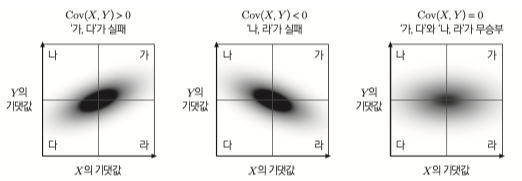
음수, 양수, 0일 때의 상황이다.

양수(양의상관관계): 서로 같이 커짐, 서로 같이 작아짐 음수(음의상관관계): 한쪽이 크면 한쪽은 작아짐, 한쪽이 작아지면 한쪽은 커짐 0(무상관): 서로 커짐과 작아짐에 별 관계가 없음

두 숫자형 변수가 같은 방향으로 움직이는 정도를 뜻한다.

즉 $x$ 값과 $y$ 값의 상관관계, $x$ 값이 변화함에 따라 $y$ 값의 변화량이 얼마나 되는지를
공분산, 상관계수, 공분산 행렬 등으로 알 수 있다.

상관계수(Correlation coefficent)

두 사건이 강한 연관성을 가질수록 공분산의 절대값은 커진다.

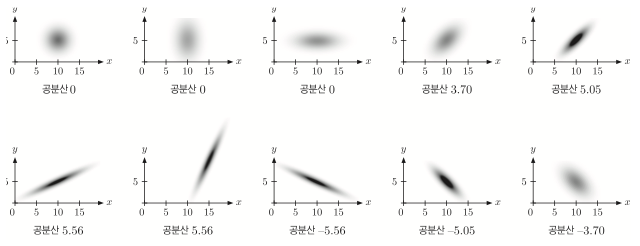
하지만 공분산값이 크다고 두 사건이 강한 연관관계를 가지고 있다고 확신은 못한다.

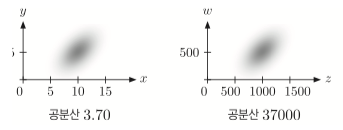
동일한 형태의 확률밀도그래프이지만 확률변수의 스케일만 100배로 키웠을 경우
공분산은 $100^2$ 배 차이가 나게 된다.

두 확률변수의 정확한 연관관계를 알기위해 공분산값을 정규화한 상관계수 를 사용한다.

상관계수: 공분산을 각각의 표준편차로 나누어준 값. 측정단위와 상관없이 두 변수간의 연관성, 직선적인 경향을 나타내줌

상관계수의 공식은 아래와 같다.

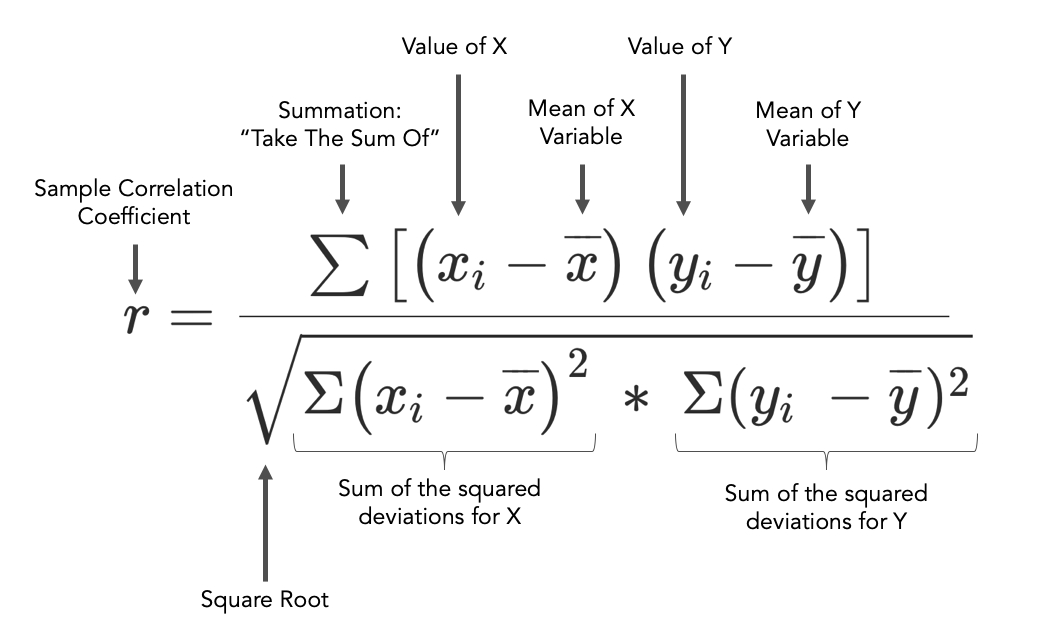
요약하면 아래

\[\rho_{XY} = \frac{Cov[X,Y]}{\sqrt{V[X]}\sqrt{V[Y]}} \\ \ \\ -1 \le \rho \le 1\]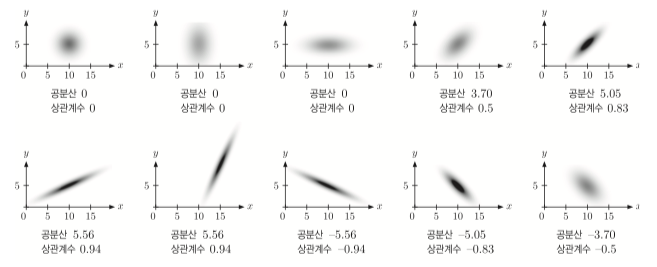

위처럼 $x, y$ 가 서로 확실한 상관성을 가지고 변화한다면 상관계수는 1에 가깝게 출력된다.

즉 상관계수는 데이터에 크기에 상관없이 얼마나 상관성이 있는지를 나타내며 힘과 방향또한 어느정도 알 수 있다.

상관계수와 백터와의 연관성

\[r=\frac{\sum[(x_i-\bar{x})(y_i-\bar{y})]} {\sqrt{\sum(x_i - \bar{x})^2\ * \sum(y_i - \bar{y})^2}}\]

$(x_i - \bar{x})$ 와 $(y_i - \bar{y})$ 를 $\vec{a}$ 와 $\vec{b}$ 변환해보자.
$x_i … x_n$ 까지의 요소가 $\vec{a}$ 의 요소로, $y_i … y_n$ 까지의 요소가 $\vec{b}$ 의 요소로 들어가게 된다.(mean 값 빼는건 생략했다)

$\vec{a} \cdot \vec{b} = \sum a_ib_i$
$\vec{a} \cdot \vec{a} = \sum a_ia_i = \sum a_i^2$ 이기 때문에

\[r=\frac{\vec{a} \cdot \vec{b}} {|\vec{a}||\vec{b}|}\]

이런식으로 상관계수 r 을 백터로 생각할 수 있다.

$(x_i - \bar{x})$ 와 $(y_i - \bar{y})$ 를 $\vec{a}$ 와 $\vec{b}$로 변경하였기 때문에 x 의 편차, y 의 편차가 얼마나 서로를 설명하는가를 뜻한다.

그리고 백터간의 내적에 백터의 길이 곱한것을 빼면 $\cos \theta$ 이기 때문에 $0 \le r \le 1$ 이 된다.

공분산 행렬(covariance matrix)

$X,Y$ 두개의 확률변수를 기반으로 공분산과 상관계수를 설명했는데
만약 3개의 확률변수 $X_1,X_2,X_3$ 가 있다면 공분산과 상관계수를 어떻게 설명해야 하는가

모든 상관계수를 2개씩 짝지어 공분산을 구하고 행렬로 표현한다.

\[\begin{pmatrix} V[X_1] & \mathrm{Cov}[X_1, X_2] & \mathrm{Cov}[X_1, X_3] \\ \mathrm{Cov}[X_1,X_2] & V[X_2] & \mathrm{Cov}[X_2, X_3] \\ \mathrm{Cov}[X_1,X_3] & \mathrm{Cov}[X_2,X_3] & V[X_3] \\ \end{pmatrix}\]

아래 같은 2차원 데이터 영어, 국어를 예로 공분산을 구해보면

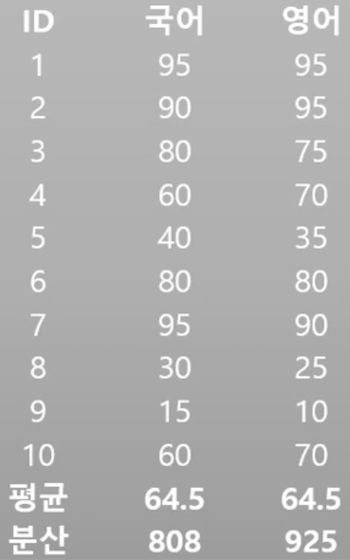
공식에 대입하면 $\mathrm{Cov_{국어,영어}} = 762$ 가 나온다.

그리고 2차원 데이터에 대한 공분산 행렬을 아래와 같다.

\[c = \begin{pmatrix} 808 & 762 \\ 762 & 925 \\ \end{pmatrix}\]

만약 3차원 이었다면 3x3 형태의 정방형 행렬이 되었을것,

위처럼 같은 데이터간의(국어x국어) 의 분산값과 다른 데이터간(국어x영어) 의 공분산값을 행렬로 만들어 놓은것을 공분산 행렬이라 한다.

공분산 행렬의 형태를 보고 대략적으로 데이터가 어떻게 분포되어 있는지 알 수 있다.

공분산은 분산과 다르게 편차의 제곱이 아닌 2개의 변수간 곱이기 때문에 음수가 나올 수 있다.

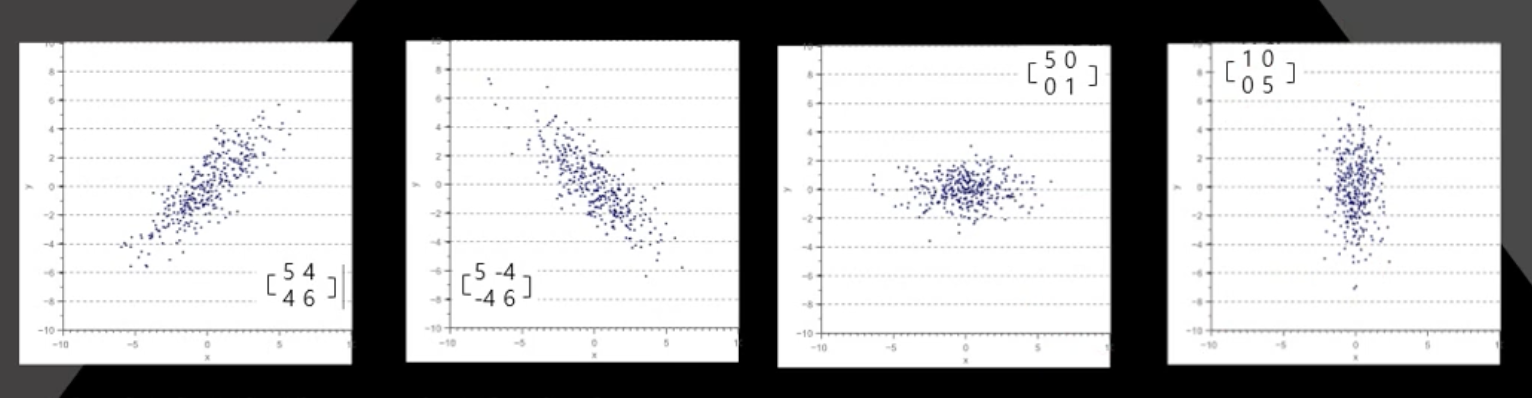
분산값을 통해 $x, y$ 값이 얼마나 퍼져있는지, 공분산을 통해 $x$의 변화량에 따른 $y$ 의 변화량을 알 수 있다.

백터 표현식

확률변수가 $X_1, \cdots , X_n$ 있을 경우
아래와 같이 확률변수들을 한개의 벡터 $\mathbb{X}$ 로 묶어 표현, 공분산 행렬을 벡터로 표기하면

\[\mathbb{X} = \begin{pmatrix} X_1 \\ X_2 \\ \vdots \\ X_n \end{pmatrix}\] \[E[\mathbb{X}] = E\left[ \begin{pmatrix} X_1 \\ X_2 \\ \vdots \\ X_n \end{pmatrix} \right] = \begin{pmatrix} E[X_1] \\ E[X_2] \\ \vdots \\ E[X_n] \end{pmatrix}\] \[\mathrm{Cov}[\mathbb{X}] = E[(\mathbb{X-m})(\mathbb{X-m})^T]\]

벡터에 대해 분산한다는것은 공분산행렬을 나타내기로 약속되어 있어 아래와 같이 표기하는 것이 정석이다.

$V[\mathbb{X}] = \mathrm{Cov}[\mathbb{X}]$

이 벡터표현식은 앞으로 설명할 공분산행렬 연산 식을 쉽게 표현하기 위해 사용된다.

주의사항

두 사건이 독립일 경우 무상관, 하지만 무상관이라고 두 사건이 독립이라고는 보장할 수 없다.

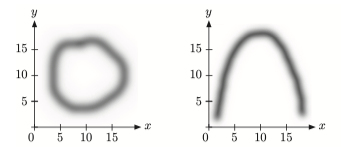
위 그래프의 공분산값은 0이지만 두 확률변수 $X,Y$ 의 뚜렷한 연관과계가 보인다.

또한 $X,Y$ 외의 또 다른 확률변수 $Z$ 의 존재가 있는지 확인해야 한다,
$(X,Y)$ 의 공분산값이 높게 나왔지만 사실 $(X,Y)$ 는 전혀 상관없는 사건이고
$(X,Z) (Y,Z)$ 의 공분산값이 높게나와서 일 수도 있기 때문

두 변수의 단위가 다를 때, 다른 값을 가지게 되는 단점이 있다.