연속확률분포 개요
연속확률분포는 아래와 같은 분포가 있다.
- 균등분포
- 정규분포
- 표준정규분포
- 가수분포
- T분포
- 카이제곱분포
- F분포
- 감마분포
- 웨이블분포
- 베타분포
확률밀도함수, 누적분포함수
확률밀도함수: PDF(Probability Density Function)
누적분포함수: CDF(Cumulative Distribution Function)
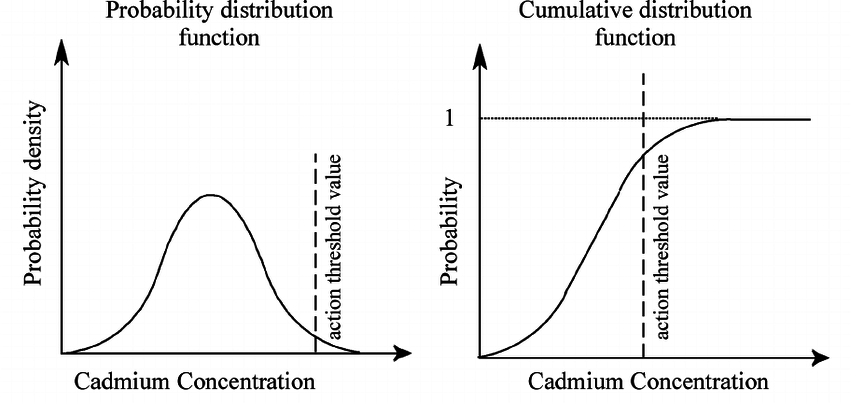
일반적인 정규분포의 경우 다음과 같이 PDF, CDF 그려진다.
연속확률분포도 마찬가지로 전체발생확률이 1이기에 PDF 의 적분이 1이고
CDF 는 확률이 계속 누적되어 더해지기때문에 가장높은값인 1로 수렴하게 된다.
이런 특성때문에 PDF 를 미분하면 CDF 함수가 출력되고
CDF 를 미분하면 PDF 가 출력된다.
연속확률분포에선 그래프이기 때문에 시그마가 아닌 인테그랄(적분식)으로 표기한다.
이산확률분포와 똑같이 각 변량 $x$에 대한 도수 $f(x)$ 의 합을 적분식으로 표기하며
f(x)의 모든 합은 1이된다.
기대값(E) 는 밀도함수의 결과값 $f(x)$ 와 연속확률 변수 $x$ 를 곱한값을 적분한 것이다.
\[E(X) = \int_a^b xf(x) dx\]분산(V) 는 편차제곱과 밀도함수의 결과값을 곱한값을 적분한것.
\[V(X) = \int_a^b (x-m)^2 f(x) dx = \int_a^b x^2 f(x) dx - m^2\]확률밀도함수의 변수변환
확률변수 $X$ 의 확률분포를 알고 있을때 변환처리를 한 확률변수 $Y$ 를 구한다면
$Y$ 의 확률분포를 어떻게 표기하는가
예를들어 확률변수 $X$ 의 확률밀도함수 $f_X$, 확률변수 $Y$ 확률밀도함수 $f_Y$ 가 있고
$Y=3X-5$ 일 경우
확률변수의 변화에 따라 아래와 같은 그래프를 그릴 수 있다.
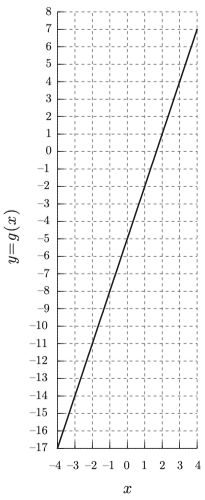
$X$ 는 -4 ~ 4 까지 총 8 칸을 사용할때
$Y$ 는 -17 ~ 7 까지 총 24 칸을 사용하였다.
총 확률 1을 8개로 나눠먹느냐, 24개로 나눠먹느냐 라고 할 수 있다.
이는 밀도가 전반적으로 3배 차이가 난다는 뜻이다.
실제 해당 확률밀도 함수가 가질 밀도는 3배 차이가 난다는 것을 식으로 표현하면 아래와 같다.
$f_Y(4) = \frac{1}{3} f_X(3)$
정형화된 공식으로는 아래와 같다.
$f_Y(y) = \left \vert\frac{f_X(x)}{g’(x)}\right \vert$
위 공식에 $f_Y$ 와 $f_X$ 를 대입하면 아래와 같이 풀어쓸 수 있다.
\[\because X = \frac{Y+5}{3} \\ \ \\ f_Y(y) = \left \vert \frac{f_X(x)}{g'(x)} \right \vert \\ \ \\ f_Y(y) = \left \vert \frac{f_X(\frac{Y+5}{3})}{3} \right \vert \\ \ \\ f_Y(y) = \frac{1}{3} f_X(\frac{Y+5}{3})\]$Y$ 에 에 값을 대입해 위 그래프와 같이 출력되는지 확인
연속확률분포 특징
결합분포, 주변분포
이산확률에서 결합확률을 아래와 같이 정의지었다.
여러 조건을 지정하고 모든 조건이 동시에 성립하는 확률을 결합확률이라 하며 동시확률이라 부르기도 한다.
연속확률분포에서 결합확률에대한 분포는 아래와 같이 말할 수 있다.
$X,Y$ 를 세트로 하는 2차원 벡터 $W=(X,Y)$ 에 대한 결합분포
그리고 $\vec{W}$ 를 확률밀도함수로 그래프로 그리면 아래와 같고 결합된 확률변수 범위안의 확률은 부피와 같다.
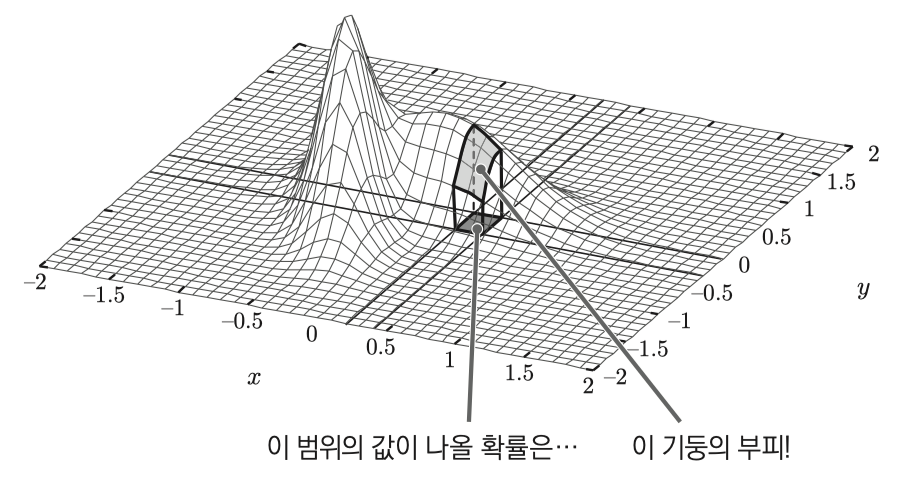
기존 확률밀도함수처럼 전 영역에서 적분하면 1이 된다.
\[\int_{-\infty}^\infty (\int_{-\infty}^\infty f_{X,Y}(x,y)dx)dy = 1\] \[\int_{-\infty}^\infty (\int_{-\infty}^\infty f_{X,Y}(x,y)dy)dx = 1\]이산확률에서 주변확률를 아래와 같이 정의지었다.
결합확률의 각 조건을 주변확률 이라 한다. $P(X, Y)$ 결합확률에서 $P(X=a), P(Y=b)$ 가 주변확률이 된다.
아래 그림과 같이 단면적의 부피를 주변확률 이라 할 수 있다
2개의 확률변수를 가진 연속확률분포에선 면적이 아닌 부피가 확률이기에
그림처럼 주변확률 하나를 고정해두면 0에 가까운 부피값이 나온다. 하지만 설명의 위해 부피가 아닌 면적을 기반으로 설명하는것을 주의

왼쪽이 $f_X(0)$, 오른쪽이 $f_Y(0.3)$ 일때의 주변확률이다 .
그리고 이 주변확률을 모두 모아 주변분포를 만들고, 그 분포의 확률밀도함수인 주변확률밀도함수 를 구하는 방식은 아래 그림과 같다.
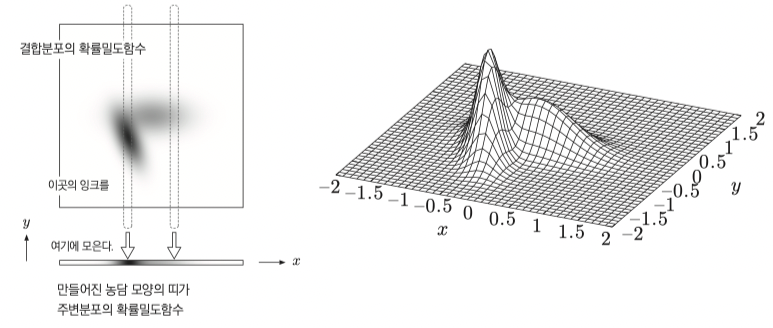
$\vec{W}$ 를 2차원에서 잉크의 농담처럼 표기하고 $y$ 축 방향을 눌러 $x$ 축 위에 모으면 $f_X(x)$ 의 주변확률밀도함수이다.
식으로 표현하면 다음과 같다.
\[f_X(x)=\int_{-\infty}^\infty f_{X,Y}(x,y)dy=1 \\ \ \\ f_Y(y)=\int_{-\infty}^\infty f_{X,Y}(x,y)dx=1\]조건부분포
이산확률에서 조건부확률은 비중에 따른 확률값 이다.
조건부확률을 결합확률로 표기하면 아래와 같다.
$P(Y=b \mid X=a) = \frac{P(Y=b, X=a)}{P(X=a)}$
연속확률에선 다시 아래의 단면적 그래프로 생각해야 한다.
이것도 마찬가지로 설명을 위해 부피가 아닌 면적을 기반으로 이야기한다.
하지만 사실 부피를 이야기하는 것임을 주의
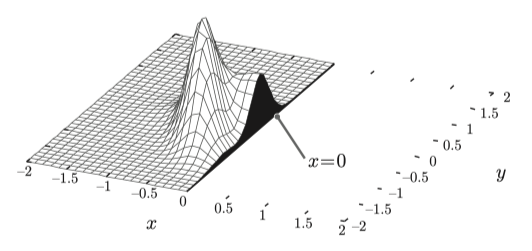
$X=0$ 이라는 조건에서 어떤 $Y$ 값이 나올지 아는것은 대략 알 수 있다.
잘린 단면의 형태를 $g(y) = f_{X,Y}(0,y)$ 라 할때 나오는 가장 높은값이 높은 확률로 나올 Y 값이다.
그럼 조건부확룰밀도함수 는 어떻게 구하는가하면 해당 단면적이 1이 되도록 만들면 된다.
현재 $g(y)$ 의 적분은 1이라 할 수 없지만 여기에 특정 상수 $c$ 를 추가해 적분값이 1이 되도록 조절한다.
아래 그림과 같이 기존 절개된 부분(굵은선)을
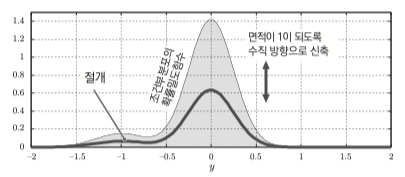
\[h(y) = \frac{g(y)}{c}\]나중에 설명하지만 이 $c$ 값이 비중이 된다.
이 $h(y)$ 값이 조건부확룰밀도함수 $f_{Y \mid X}(b \mid A)$ 이다.
$h(y)$ 의 단멱적이 1 이기에 적분식은 아래와 같고
\[\int_{-\infty}^\infty h(y)dy = \frac{1}{c}\int_{-\infty}^\infty g(y)dy = 1\]이는 $\int_{-\infty}^\infty g(y)dy$ 값이 $c$ 와 동일해지는것을 의미,
그리고 $\int_{-\infty}^\infty g(y)dy$ 를 주변분포로 표기하여 유도하면 $f_X(a)$ 와 동일해진다.
\[c = \int_{-\infty}^\infty g(y)dy = \int_{-\infty}^\infty f_{X,Y}(a,y)dy = f_X(a)\]$y$ 에 대해 적분하였으니 확률변수 $Y$ 는 제외하고 확률변수 $X=a$ 발생확률만 따지면 된다.
그래서 최종적으로 조건부확룰밀도함수 $f_{Y \mid X}(b \mid A)$ 를 표기하는 식은 아래와 같다.
\[h(y) = \frac{g(y)}{c} = \frac{f_{X,Y}(a,y)}{f_X(a)} \\ \ \\ f_{Y \mid X}(b \mid A) = \frac{f_{X,Y}(a,y)}{f_X(a)}\]이산확률과 마찬가지로 결합확률밀도함수를 조건부확률밀도함수로 표현할 수 있다.
\[f_{X,Y}(a,b) = f_{Y \mid X}(b \mid A)f_X(a)\]베이즈공식
베이즈이론: 조건부확률을 응용해서 결과에서 원인을 찾는 경우 $P(X=▲), P(Y=○ \mid X=▲)$ 를 알고 있을때 $P(X=▲\mid Y=○)$ 조건부확률을 구하는 것을 베이즈 공식이라 한다.
이산확률에서 베이즈공식은 조건부확률과 결합확률의 관계를 통해 아래와 같은 식을 통해 구할 수 있었다.
\[P(A \mid B) = \frac{P(A , B)}{P(B)} = \frac{P(B \mid A)P(A)}{\sum_x P(B,x)} = \frac{P(B \mid A)P(A)}{\sum_x P(B \mid x)P(x)}\]연속확률에선 $\sum$ 을 $\int$ 로만 변경해주면 된다.
\[f_{X,Y}(A \mid B) = \frac{f_{Y,X}(B \mid A)f_X(A)}{\int_{-\infty}^\infty f_{Y,X}(B \mid x)f_X(x)dx}\]독립성
이산확률에서 두 사건 발생이 서로 독립일 때 아래 공식들이 만족한다.
- $P(A \mid B) = P(A)$
- $P(A \mid B) = P(A \mid B^c)$
- $P(A,B) = P(A)P(B)$
- $P(A,B):P(A,B^c) = P(A^c,B):P(A^c,B^c)$
연속확률도 그대로 사용하면 된다.
그래프로 표기하며 아래와 같다.
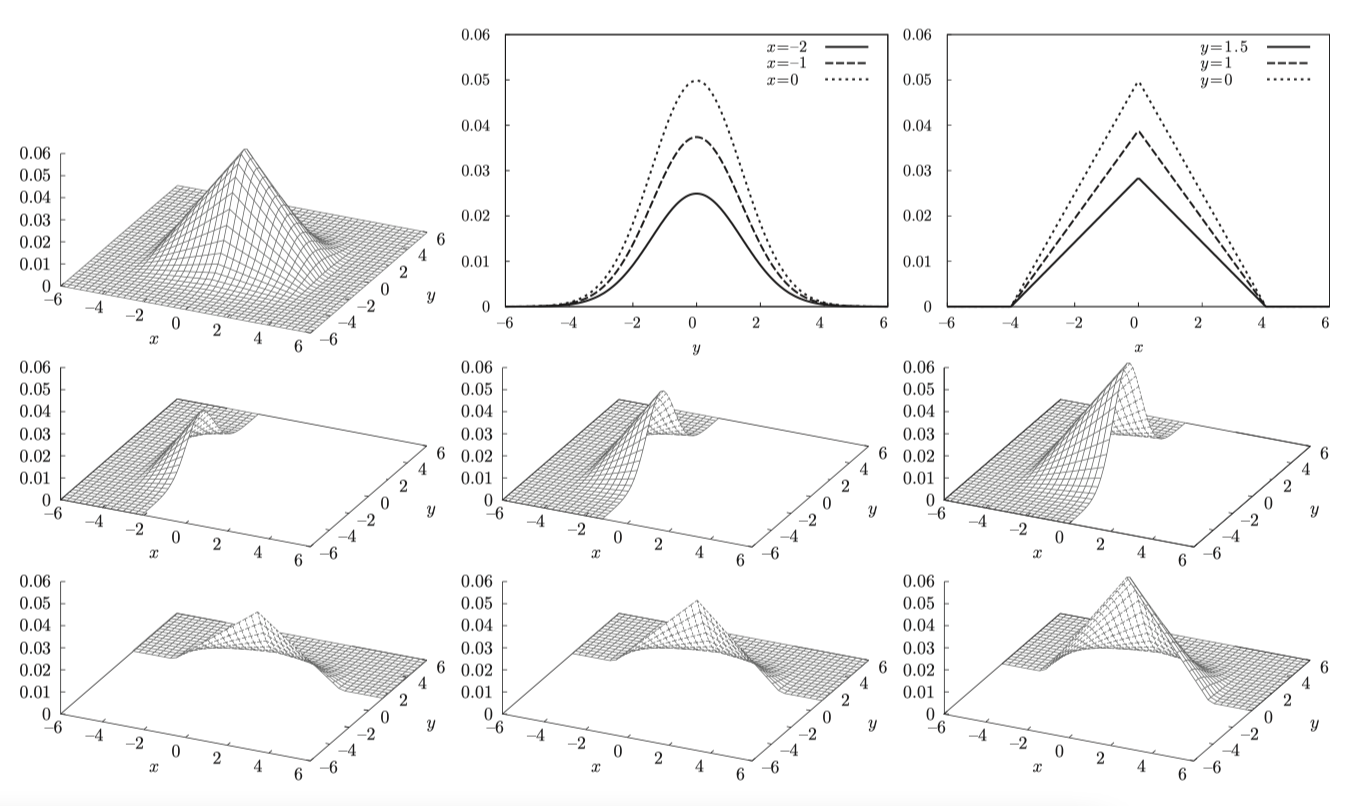
잘린 단면의 모양이 높이값을 제외한다면, 완벽히 일치할 경우 독립이라 볼 수 있다.
$f_{X,Y}(a,y) = c f_{X,Y}(\hat{a}, y)$ $f_{X,Y}(x,b) = c f_{X,Y}(x, \hat{b})$ 위 식과 같이 어떤 $X$ 혹은 $Y$ 가 고정되어 있는 상태에서 상수 $c$ 를 곱하면 일치할 경우 식이 일치할 경우
조건부분포의 경우 단멱적이 1이 되도록 변환해야하기에 값의 차이가 상수 $c$ 차이라면 최종 출력되는 확률값은 모두 동일하다 할 수 있다.
변수변환
확률변수 $X,Y$ 그리고 변환된 확률변수 $Z=2X, W=Y$ 로 변환, 혹은 $Z=X, W=1.5Y$ 로 변환했을 때
$f_{X,Y}(x,y)$ 와 $f_{Z,W}(z,w)$ 의 관계는?
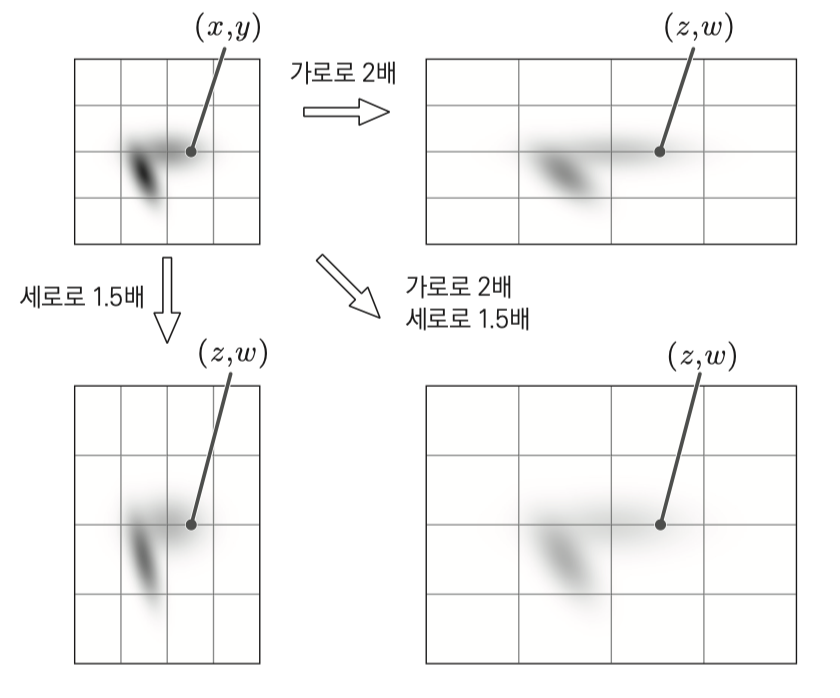
아파 확률별수 사이즈를 일방적으로 늘리면 위 그림과 같이 잉크의 농도가 옅어질 것이다.
범위가 늘어난다 한들 부피는 1을 유치해야하지 때문에 늘어난 범위만큼 높이가 줄어들 것
따라서 $Z=2X, W=Y$ 로 변환되었다면
$f_{Z,W}(z,w) = \frac{1}{2}f_{X,Y}(\frac{1}{2}z,w)$ 관계를 가지게 된다.
기대값, 분산, 표준편차
연속확률에서 기대값 역시 이산확률의 $\sum$ 을 $\int$ 로 변경하기만 하면 된다.
\[E[X] = \int_{-\infty}^\infty x f(x) dx\]수식으로만 생각하면 연속된 확률변수 $x$ 와 해당 확률변수에서 발생가능한 확률 $f(x)$ 를 모두 $\int$ 하면 기대값이 나온다.
$ V[X] = E[(X - m)^2]$
$\sigma = \sqrt{V[X]}$
연속확률이라 해도 이산확률의 기대값, 분산, 표준편차와 차이 $\sum, \int$ 만 있을뿐 수식에는 없다.