이산확률분포 개요
확률분포는 크게 이산확률분포, 연속확률분포 2가지로 나뉜다.
여기선 이산확률분포에 대해 알아본다.
이산(離散)값, discrete value(흩어져있는 값), 연속성이 전혀 없는 분리된 상태를 뜻한다.
이산확률분포는 확률변수가 셀 수 있는 제한된 개수(자연수)로 구성된다.
이산확률분포에는 아래 종류의 분포가 있다.
- 베르누이분포
- 이항분포
- 기하분포
- 음이항분포
- 포아송분포
- 초기하분포
- 다항분포
이산확률에서의 기대값,분산를 알아보자.
변량은 $x_1, x_2, …, x_n$, $x$가 취할수 있는 값, 통틀어 $X$ 로 표시 도수는 $p_1, p_2, …, p_n$, 각 $x$ 에 대한 확률, 통틀어 $P$ 로 표시한다.
눈이 6개인 주사위를 5번 굴려 1이 0개 ~ 5개 나올 확률을
확률분포표로 나타내면 아래와 같다.
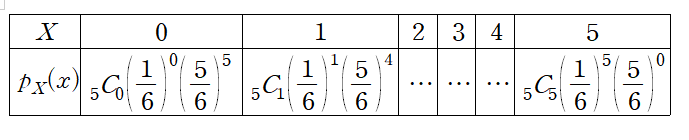
변량, 도수가 정해져 있고 이를 표로 나타낸게 도수분포표 라면
확률을 가지고 표로 나타낸게 확률분포표 이다.
예로 눈 1이 5번 나올 확률은 $P_5=_5C_5(\frac{1}{6})^5(\frac{5}{6})^0$ 이다.
확률분포표의 특징중에 하나는 모든 확률을 더하면 1이 나온다는 점
확률분포표의 도수는 곧 확률이기 때문에 일어날 수 있는 모든 도수의 합은 1이다
기대값(mean) 과 분산(variance) 공식
도수의 합이 1이다 보니 평균, 분산을 구하는 식도 분모가 1이되다 보니 생략 가능하다.
\[E(X) = m = \frac{\sum_{k=1}^nx_kp_k}{\sum_{k=1}^n p_k} = \sum_{k=1}^n x_kp_k\] \[V(X) = \sigma^2 = \frac{\sum_{k=1}^n (x_k - E(X))^2p_k}{\sum_{k=1}^n p_k} = \sum_{k=1}^n (x_k - E(X))^2p_k\]분산은 기존 $p_k$ 값에서 기대값 $E(X)$ 을 뺀 것을 제곱한 후 모두 더하고 다시 기대값을 낸 값이다.
그래서 분산은 정도를 벗어난 기대값 이라 할 수 있다.
이산확률분포의 평균, 분산의 성질
대부분의 공식이 아래 2개로 변환하여 유도된다.
$\sum_{k=1}^n x_k \cdot pk = E(X)$
$\sum_{k=1}^n pk=1$
분산은 평균값으로 유도되는 식이기에 분산=제평-평제(제곱의평균-평균의제곱) 라는 공식으로도 구할 수 있다.
$V(X) = E(X^2) - E(X)^2$
아래 공식으로 유도된다.
\[\begin{aligned} V(X) &= \sum_{k=1}^n (x_k - E(X))^2p_k \\ &=\sum_{k=1}^n (x_k^2 - 2E(X)x_k + E(X)^2)p_k \\ &=\sum_{k=1}^n x_k^2p_k - \sum_{k=1}^n2E(X)x_kp_k + \sum_{k=1}^nE(X)^2p_k \\ &=\sum_{k=1}^n x_k^2p_k - 2E(X)\sum_{k=1}^nx_kp_k + E(X)^2\sum_{k=1}^np_k \\ &=\sum_{k=1}^n x_k^2p_k - 2E(X) \cdot E(X) + E(X)^2\\ &= E(X^2) - E(X)^2 \end{aligned}\]확률변수를 $X \to aX+b$ 로 변경할때 평균, 분산, 표준편차는 아래와 같은 성질을 갖는다.
\[\begin{aligned} E(aX+b) &\to aE(X)+b \\ \\ V(aX+b) &\to a^2V(X) \end{aligned}\]$E(aX+b)$ 가 어떻게 $aE(X)+b$ 가 되는지 알아보자.
\[\begin{aligned} E(aX+b) &= \sum_{k=1}^n (ax_k + b)p_k \\ &= \sum_{k=1}^n (ax_k \cdot pk + b \cdot pk) \\ &= a\sum_{k=1}^n x_k \cdot pk + \sum_{k=1}^n b \cdot pk \\ &= a\sum_{k=1}^n x_k \cdot pk + b\sum_{k=1}^n pk \\ &= aE(X)+b\\ \end{aligned}\]$V(aX+b)$가 어떻게 $a^2V(X)$ 가 되는지 알아보자.
분산은 확률변수 $X$ 에 평균 $E(X)$을 뺀 제곱값의 평균임으로 아래 식으로도 나타낼 수 있다.
여기서 $E(…)$ 는 상수임으로 $\sum$ 영향을 받지 않음
식을 정리하면 아래처럼 변경된다.
\[\begin{aligned} V(aX + b) &= \sum_{k=1}^n (ax_k - aE(X))^2p_k \\ &= \sum_{k=1}^n a^2(x_k - E(X))^2p_k \\ &= a^2\sum_{k=1}^n (x_k - E(X))^2p_k \\ \\ \end{aligned}\]a^2 뒤에 있는 공식이 V(X) 의 공식이기 때문에
$ V(aX + b) = a^2V(X) $ 이다.
표준편차는 분산의 제곱근임으로 생략 $S(aX+b) \to |a|S(X)$
분산 - 그래프로 보기
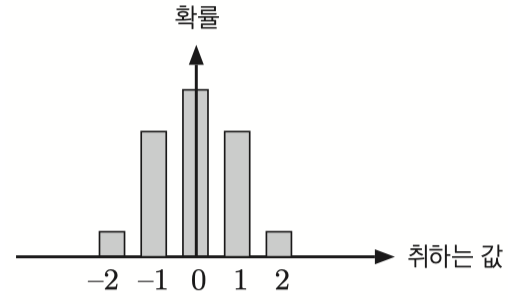
위와같은 형태의 음수가 포함된 확률변수 $X$ 가 있을 때
$E(X^2)$ 은 $X$ 확률변수중 음수였던 값들은 양수로 변화되고
편차의 제곱만큼 증가한다고 볼 수 있다.
해당관점으로 보기위해 위 식의 순서를 바꿔보면
$V(X) = E(X^2) - E(X)^2$ $E(X^2) = E(X)^2 + V(X)$
$X^2$ 의 기대값은 ($X$ 의 기대값의 제곱 + 분산) 만큼 늘어난다고 볼 수 있다.
상수 $c$ 와 확률변수 $X$ 에 아래와 같이 연산할 수 있다.
$V[X+c] = V[X]$ 정수 c 를 합해도 분산은 다름없다.
$V[cX] = c^2V[X]$ 상수를 곱하면 차의 제곱이기에 $c^2$ 해야한다.
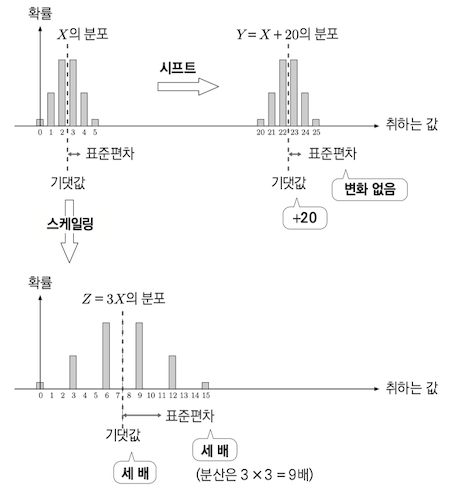
표준편차 - 불균형의 정도
만약 0 ~ 30 까지 무작위 숫자를 출력하는 난수발생기가 있을경우
분산은 비거리 차이의 제곱 의 기대값이다.
길이의 제곱은 비교하기에는 너무 큰 차이기 때문에 일반적으로 제곱근을 사용한 표준편차 를 사용해서 비교한다.
아래 그래프의 좌측은 분산이 25, 우측은 분산이 100 인 경우이다.
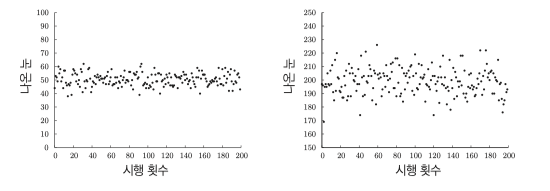
분산은 4배차이이지만 세로축으로 2배정도 스케일업한 느낌이다.
실제 분산값이 100이라고 기댑갓에 100 벗어난 값이 나오는 것은 아니다.
실제 우측 그래프의 가장 낮은값은 170, 높은값은 225 정도, 둘의 차이는 50 밖에 나지 않는다.
이래서 실제 데이터를 비교할때는 표준편차를 사용한다.
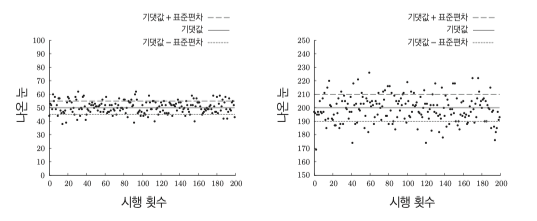
세로축에 표준편차에 해당하는 값을 그렸는데 대부분 해당 라인 안에 데이터가 분포되어 있다.
해당 표준편차를 벗어난 값을 불균형적인 데이터라 할 수 있음으로 표준편차를 불균형의 정도 로 생각할 수 있다.
이산확률변수 특징
조건부 기대값
| $X=a$ 라는 관측값을 얻었을 때 $Y=b$ 를 예측하려면 $P(Y=b | X = a)$ |
하지만 확률분포에선 상수 $b$ 를 예측하는게 아니라 가장 높은확률로 나올수 있는 기대값 $b$ 를 예측해야 한다.
이를 조건부 기대값이라 한다.
\[E[Y \mid X = a] = \sum_b b \times P(Y=b \mid X=a)\]최소제곱 예측
조건부 기대값은 최소제곱 예측이라는 특성을 가지고 있다.
$P(Y=b \mid X=a)$ 조건부분포가 있다.
확률변수 $X$ 에 값을 넣으면 $Y$ 의 추정값(전망값) $\Delta$ 출력되는 프로그램이 있을 때
$g(X=a) = \Delta$
확률변수 $Y$ 와의 제곱오차의 기대값 $E[(Y - g(X))^2]$ 을 가장 작게하려면
$g(X)$ 는 어떤 함수가 되어야 하는가?
정답은 입력된 확률변수에 대한 조건부 기대값이다.
$g(X) = E[Y \mid X=a]$
표본평균, 표본분산
모집단에서의 평균, 분산이 아닌
표본에 대해서 평균과 분산을 구하는 공식은 따로 있는데 아래와 같다.
bar 를 사용해 표본임을 표기한다.
표본평균: $\bar{X} = \frac{1}{n}\sum^n_{i=1}x_i$ 표본분산: $s^2= \frac{1}{n-1}\sum^n_{i=1}(x_i - \bar{x})^2$ 표본표준편자: $s$
자유도 (Degree Of Freedom)
$x_1 + x_2 + x_3 = 10$
각 독립변수 x 에 대해 자유롭게 값을 설정할 수 있다.
이렇게 자유롭게 선택가능한 독립변수의 개수를 자유도라 한다.
하지만 위의 경우 $x_1$ 과 $x_2$ 가 결정되면 $x_3$ 은 선택권이 없다.
따라서 위의경우 자유도는 2라 할 수 있다.
표본 $x_n$ 그리고 표본의 평균 $\bar{x}$ 가 있을 경우 둘의 편차의 합은 당연히 0이다.
$\sum(x_i - \bar{x}) = 0$
$\bar{x}$ 는 상수이기에 모두 오른쪽으로 넘기면
$x_1 + x_2 + \cdots + x_n = n \cdot \bar{x}$
이때 합을 $n \cdot \bar{x}$ 으로 만들기 위해 선택할 수 있는 $x_i$ 의 개수(자유도) 는 $n-1$ 개가 된다 (마지막 독립변수는 선택불가능함으로)
모집단에서 표본을 추출할 경우 중심에 있는 표본들이 추출될 확률이 높고
이렇게 중심값에 가까운 표본들의 분산값은 모집단의 분산보다 작다.
표본분산 n-1 이유
모집단과 표본의 분산의 차이를 줄이기 위해 $n$ 이 아닌 자유도로 나누는 것
(물론 그렇다고 해서 모집단과의 간극이 줄어들뿐 일치하진 않는다)
표본을 $X_1, X_2, \cdots, X_n$ 개, 많이 만들어 기대값을 만든다.
표본평균의 기대값 $E(\bar{X})$ - 표본을 여러개 뽑아 여러개 표본의 기대값
표본분산의 기대값 $E(s^2)$ - 표본을 여러개 뽑아 여러개 분산의 기대값
우리는 직관적으로 표본평균의 기대값, 표본분산의 기대값이 모집단의 평균과 분산과 같을것이라고 추정할 수 있다.
\[E(s^2) = E\left( \frac{1}{n-1} \sum (X_i - \bar{X})^2 \right) = \sigma^2\]