수학 - 확률 개요!

용어

도수분포표

도수분포표를 통해 통계에서 사용하는 평균, 편차, 분산, 표준편차를 알아보자.

$1$

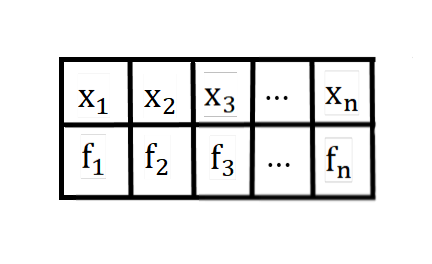
변량 - 자료를 숫자로 나타냄
$x_1, x_2, …, x_n$, 통틀어 $X$ 로 표시한다.
도수 - 자료의 수 각 계급에 속하는 $f_1, f_2, …, f_n$, 통틀어 $Y$ 로 표시한다.

학생점수를 도수분포표로 나타내면

변량: 0~100 까지 점수
도수: 각 점수에 속하는 학생의 수

기대값(mean)

평균은 모든 변량과 도수를 서로 곱하고 더한 후 도수만큼 나눈다.
여기서 $\sum_{k=1}^n f_k = n$ 으로 변환하여 사용한다.

\[m = \frac{\sum_{k=1}^n x_kf_k}{\sum_{k=1}^n f_k} = \frac{1}{n} \sum_{k=1}^n x_kf_k =E(X)\]

평균은 기댓값(expactation) 으로 말하기도 하며 위의 수식으로 표기한다.

편차(deviation)

\[x_k - m\]

편차는 변량 하나와 평균을 뺀 값이다. 음수 혹은 양수일 수 있다.

분산(variance)

분산은 각 변량들이 평균과 얼마나 떨어져 있는지를 알기 위한 값이다.
그래서 분산은 정도를 벗어난 기대값 이라 할 수 있다.

값이 얼마나 고르게 분포되어 있는지 아니면 밀집되어 분포되어 있는지 알수있다.

\[\sigma^2 = \frac{\sum_{k=1}^n (x_k - m)^2f_k}{\sum_{k=1}^n f_k} = \frac{1}{n}\sum_{k=1}^n(x_k - m)^2f_k =V(X)\]

편차의 제곱과 도수를 곱하고 평균을 구해 값들이 평균에 밀집해 있는지 아닌지를 판단 가능하다.

표준편차(standard deviation) 분산 $V(X)$ 의 제곱근이다.

\[\sigma = S(X)\]

확률분포 개요

눈이 6개인 주사위를 5번 굴려 1이 0개 ~ 5개 나올 확률을
확률분포표로 나타내면 아래와 같다.

$2$

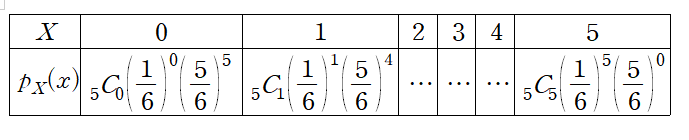
변량, 도수가 정해져 있고 이를 표로 나타낸게 도수분포표 라면
확률을 가지고 표로 나타낸게 확률분포표 이다.

예로 눈 1이 5번 나올 확률은 $P_5=_5C_5(\frac{1}{6})^5(\frac{5}{6})^0$ 이다.

확률분포표의 특징중에 하나는 모든 확률을 더하면 1이 나온다는 점
확률분포표의 도수는 곧 확률이기 때문에 일어날 수 있는 모든 도수의 합은 1이다

\[\sum_{k=1}^nP_k = 1\]

확률변수

변수 $w$ 를 입력하면 해당 변수의 확률이 출력되는 함수 $f(w)$ 가 있을때
변수 $w$ 들의 집합을 확률변수라 한다.
일반적으로 확률변수는 $X(w)$ 대문자로 표기한다.

확률변수 $X(w)$ 의 각 원소가 $w=(u,v)$ 2개의 실수, 아래 그림의 범위를 가질때(각 최소/최대값 0/1)
그림과 같이 당첨과 탈락으로 나눈다 가정하자.

$1$

\[X(u,v) = \begin{cases} 당첨 & (0 \le v \le \frac{1}{4}) \\ 탈락 & (\frac{1}{4} \le v \le 1) \end{cases}\] \[Y(u,v) = \begin{cases} 당첨 & (2u + v \le 1) \\ 탈락 & \mathrm{else} \end{cases}\]

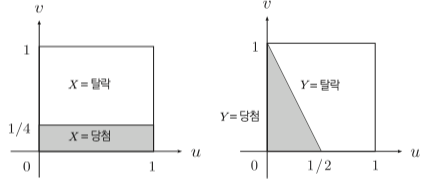
확률변수 $X$ 에서는 $u$ 값과 상관 없이 당첨되며 당첨 면적은 $\frac{1}{4}$ 또 다른 경우의 확률변수 $Y$ 애서는 $2u+v$ 를 입력값으로 받으며 당첨면적은 마찬가지로 $\frac{1}{4}$ 이다.

두 확률변수의 결과값은 같지만 동일한 확률변수라고 할순 없다.

확률분포

확률변수가 확률적으로 출력될수 있는 입력값이라면 확률분포는 대략적으로 면적만을 신경 쓰는 개념이다.

$1$

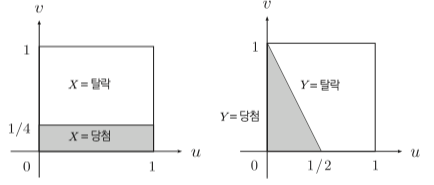
위의 $X, Y$ 에 대한 확률변수의 확률분포는 아래와 같다.

\[P(X=k) = \begin{cases} \frac{1}{4} & k=당첨 \\ \frac{3}{4} & k=탈락 \end{cases}\] \[P(Y=k) = \begin{cases} \frac{1}{4} & k=당첨 \\ \frac{3}{4} & k=탈락 \end{cases}\]

두 확률변수는 다르지만 확률분포는 같다.

즉 확률분포는 $X(w)=k$ 가 될 확률(영역의 면적) 를 정렬한 목록 을 뜻한다.

확률분포의 모든 합은 반드시 1이며 [$P(\Omega)=1$]

대부분 확률분포 기호는 $P(X=k)$라 하지 않고 생략해서 $P(k)$로 사용한다.

하지만 $X(w)$가 $k$가 되는 면적임을 항상 잊지 말자

또 모든 확률은 절대 겹치지 않는다.

$1$

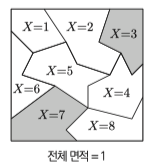
동시에 일어난다는 전제라 하더라도 그림처럼 별도의 공간으로 분리하고 아래 식으로 표현한다.

$P(X=3 \ or \ X=7) = P(X=3) + P(X=7)$

조건부확률(given), 획일확률(uniform)

$1$

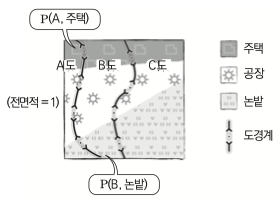
조건부확률의 계산을 위해 간단한 예를 들어보자.

경계선을 기반으로 A, B, C 구역으로 나누고 각 구역에는 주택, 공장, 논밭이 있다.

그리고 아래와 같이 총 면적 $\Omega=1$ 을 나누어 계산할 수 있다.

\[P(A,주택) + P(A,공장) + P(A,논밭) + \\ P(B,주택) + P(B,공장) + P(B,논밭) + \\ P(C,주택) + P(C,공장) + P(C,논밭) =1\]

여기서 A구역인 $P(A)$ 만 따로 때어 비중으로 계산할 수 있다.

$P(주택 \mid A) = \frac{P(A,주택)}{P(A)}$

| 기호는 조건부확률 기호이며 주어진 비중이라 할 수 있다.

A구역내 주택이 차지하는 면적비중을 구하였고
비중으로 계산했기 때문에 아래 식이 성립한다.

$P(주택 \mid A) + P(공장 \mid A) + P(논밭 \mid A) = 1$

또 주택이 차지하는 비중과 $P(A)$의 면적을 곱하면 면적이 나온다.

$P(A,주택) = P(주택 \mid A) P(A)$

이번엔 A,B,C 구역 기준이 아닌 주택, 공장, 논밭 기준으로 면적과 비중을 구해보자.

$P(A \mid 공장) = \frac{P(A,공장)}{P(공장)}$

전체 공장 면적중 A구역이 차지하는 비중을 알 수 있다.

이번엔 획일확률 에 대해 알아보자.

$1$

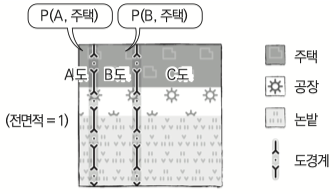
위 그림처럼 각 도가 똑같은 비율 로 주택, 공장, 논밭을 할당했을 때

각 구역별 시설의 비중은 동일할 것이다.

$P(주택 \mid A) = P(주택 \mid B) = P(주택 \mid C)$

각 시설별 구역의 비중을 구해도 동일하다
모든 시설에서 A구역이 할당하는 비중은 10%정도 일 것이다.

$P(A \mid 주택) = P(A \mid 공장) = P(A \mid 논밭)$

전체 면적 기준으로 시설 비중을 구해도 같을 것이다.

\[P(주택 \mid A) = P(주택) \\ P(A, 주택) = P(A)P(주택)\]

지금까지 이해하기 편하게 하기 위해 시설과 구역으로 나누어 면적을 기준으로 계산했지만
구역과 시설은 단순 $P$의 확률변수 일 뿐이다.

결합확률, 주변확률

여러 조건을 지정하고 모든 조건이 동시에 성립하는 확률을 결합확률이라 하며 동시확률이라 부르기도 한다.

다시 위의 예제를 이용해 구역을 확률변수 $X$, 시설을 확률변수 $Y$ 로 생각했을 때 결합확률은 $P(X=a, Y=b)$ 혹은 $P_{X,Y}(a,b)$ 로 표기한다.

결합확률의 각 조건을 주변확률 이라 한다. $P(X=a), P(Y=b)$ 등이 주변확률이 된다.

결합확률과 주변확률의 관계는 아래와 같다.
$P(X=a) = \sum_b P(X=a, Y=b)$ $P(Y=b) = \sum_a P(X=a, Y=b)$

$\sum_b$ 는 $a$는 고정이고 $b$가 계속 변한다는 뜻

결합확률은 전체구역을 기준으로 잡고 비중을 구하고
조건부확률을 특정 구역을 기준으로 잡고 비중을 구한다.
조건부확률은 확률변수옆에 | 기호를 사용하고 결합확률은 , 기호를 사용한다.

결합확률, 조건부확률의 차이는 비중을 두는 기준의 차이이다. 신의 관점으로 면적 1 기준으로는 둘의 차이는 없다.

조건부분포를 결합분포로 표현하면 아래와 같다.
$P(Y=b \mid X=a) = \frac{P(Y=b, X=a)}{P(X=a)}$

결합분포를 조건부분포로 표현하면 아래와 같다.
$P(Y=b, X=a) = P(Y=b \mid X=a)P(X=a)$

조금만 생각해보면 결합분포란

조건 $a$ 가 일어날 상황과
$a$ 가 일어난 상황에서 $b$ 가 일어난 상황

두 확률을 곱한것임을 알 수 있다.

만약 주변확률이 3가지 라면?

$P( X=a,Y=b,Z=c) = P(X=a\mid Y=b,Z=c)P(Y=b \mid Z=c)P(Z=c)$

우측 끝부터 해석하면

$c$가 일어나고
$c$가 일어난후 $b$가 일어나고
$c, b$ 가 모두 일어나고 $a$가 일어난 상황

차례대로 곱한것이다.

그림으로 예를 들어보면 아래와 같다.

$1$

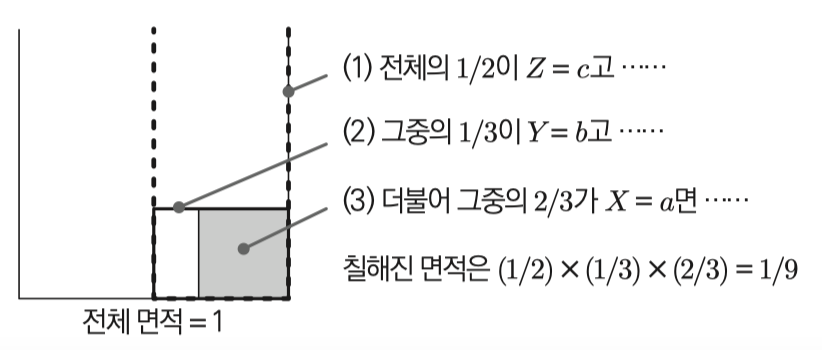
주변확률인 3개일 때 조건부분포를 분해할 수 도 있다.

$P(X=a,Y=b \mid Z=c)=P(X=a\mid Y=b,Z=c)P(Y=b \mid Z=c)$

독립성

독립성: Independent Component 확률변수 $X=a, Y=b$ 가 독립적일때 확률변수 $X, Y$ 는 독립되어 있다.
반대로 독립이 아닐경우 종속 이라 한다.

B 발생후 업데이트된 A가 발생할 확률이 A가 그냥 일어나는 확률이나 같다는 것. 즉 B 발생여부가 A의 확률에 전혀 영향을 끼치지 않는다 는 것이다.

두 사건 발생이 서로 독립일 때 아래 공식들이 만족한다.

$P(A \mid B) = P(A)$
$P(A \mid B) = P(A \mid B^c)$
$P(A,B) = P(A)P(B)$
$P(A,B):P(A,B^c) = P(A^c,B):P(A^c,B^c)$

예제) 트럼프
트럼프카드 52장을 예로 들어보자.

$P(\mathrm{spade})=\frac{1}{4}$ 스페이드를 뽑는것
$P(\mathrm{picture})=\frac{9}{52}$ 그림을 뽑는것

두 조건이 독립인지 확인해보면 아래와 같다.

$P(\mathrm{picture \mid spade}) = \frac{3}{13}$
$P(\mathrm{picture \mid spade}^c) = \frac{9}{39} = \frac{3}{13} $

스페이드에서 그림을 뽑든, 스페이드가 아닌것에서 그림을 뽑든 두 확률은 서로 같기에 독립이다.
그림으로 비교하면 아래와 같다

$1$

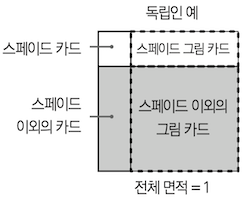
스페이드 그림카드와 스페이드 이외의 그림카드 의 비율이 정확히 일치한다.
즉 스페이드에서 그림을 뽑든, 전체에서 그림을 뽑든 동일하기에 둘은 독립변수이다.

이번에 스페이드 1,2,3 카드와 하트의 J,Q,K, 총 6장을 제거하여 독립성을 깨보자.
공식으로 나타내면 아래와 같다.

\[\begin{cases} P(\mathrm{picture \mid spade}) = \frac{3}{46} \\ P(\mathrm{picture, spade})=\frac{10}{46} \times \frac{9}{46} = \frac{1.956}{46} \end{cases}\]

그림을 그리면 아래와 같다.

$1$

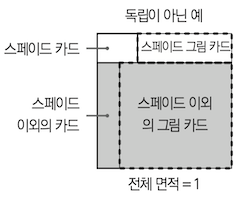
공식 활용 예제
표 혹은 수식이 주어지면 독립인지 확인할때 가장 많이 사용하는 공식은 아래 2개

$P(A,B) = P(A)P(B)$
$P(A,B):P(A,B^c) = P(A^c,B):P(A^c,B^c)$

아래와 같은 식이 있다 해보자.

$P(X=a, Y=b) = \frac{1}{280}a^2(b+1)$

1번 공식을 사용하면

$X$관련된 식은 $\frac{1}{280}a^2$,
$Y$관련된 식은$(b+1)$

두 확률변수가 1번 공식과 유사하다는것을 알수 있고 $X, Y$ 가 독립임을 바로 알 수 있다.

$1$

2번 공식을 사용하면 표를보고 $X, Y$ 의 결합분포 비율이 모두 같은걸 보고 서로 독립임을 바로 알 수 있다.

3개 이상의 독립성 확률변수가 2개가 아니라 3개일 경우 $P(X=a,Y=b,Z=c)=P(X=a)P(Y=b)P(Z=c)$ 를 만족한다.
4개일 경우에도 마찬가지

베이즈 이론

조건부확률을 응용해서 결과에서 원인을 찾는 경우 베이즈 이론을 많이 사용한다. (역문제 찾기)

소음이 들어간 신호 $Y$ 에서 전하고자 하는 송신내용 $X$ 를 찾을 때
이미지 데이터 $Y$ 에서 문자 $X$ 를 찾을때

예를들어 2/3은 함정, 1/3 은 보물상자를 뽑는 게임에서 3/4 확률로 진실을 말하는 마법이 있을경우
마법을 믿고 카드를 뽑았을 때 함정일 확률을 구해보자.

확률변수 $X$ 는 카드가 보물인지 함정인지,
확률변수 $Y$ 는 마법이 알려준 카드의 내용이다.

$P(X=함정) = \frac{2}{3}
P(Y=보물 | X=함정) = \frac{1}{4} \ P(Y=함정 | X=보물) = \frac{1}{4} $

$Y$ 와 $X$ 의 결과가 다를 확률은 $\frac{1}{4}$

위와 같이 조건부확률을 구할 수 있는데 우리가 구해야 할건 아래 식의 결과이다.

$P(X=함정

Y=보물) = ?$

진실마법은 보물이라 했지만 함정이 나오는 결과이다.

즉 베이즈 이론은 사전확률 $P(원인)$과 $P(결과	원인)$ 이 주어졌을때
사후확률 $P(원인	결과)$ 를 구하는 이론이다.

$1$

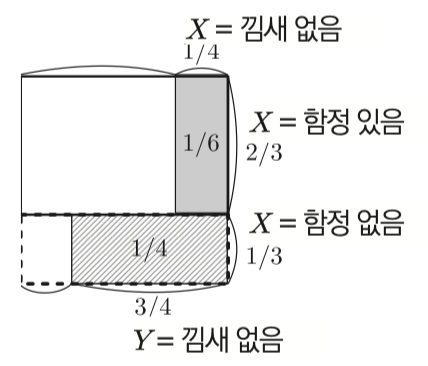
위 조건부확률을 표시한 그림이다.

세로축이 함정의 유무 가로축은, 그중 $Y$ 가 보물이라고 답할 확율이다.

전체면적 1에서 $\frac{1}{6}, \frac{1}{4}$ 가 마법을 사용했을때 낌새가 없다고 답할 면적이다.

\[P(Y=보물) = \frac{1}{6} + \frac{1}{4} = \frac{5}{12}\]

사실 $\frac{5}{12}$ 면적중에서 $\frac{1}{6}$ 은 함정이다.

\[P(X=함정 | Y=보물) = \frac{\frac{1}{6}}{\frac{5}{12}} = \frac{2}{5} = 0.4\]

마법만 믿고 카드를 골랐다가는 40% 확률로 함정을 뽑게 된다.

베이즈이론 공식

$P(X=▲), P(Y=○	X=▲)$ 를 알고 있을때
$P(X=▲	Y=○)$ 조건부확률을 구하는 것을 베이즈 공식이라 한다.

다시한번 조건부분포와 결합분포의 관계식을 보면 아래와 같다.

$ P(A

B) = \frac{P(A , B)}{P(B)} $

베이즈 공식을 사용해 $P(A

B)$ 를 구하는 식은 아래와 같다.

물론 $P(B A), P(A), P(B)$ 를 사전에 알고 있어야 최종적으로 $P(A B)$ 를 구할 수 있다.

모든 조건에서 $B$ 가 나올 범위를 풀어서 식에 대입하였다.
분모에 있을 결합분포를 조건부분포로 분해하면 최종적으로 아래 식이 나온다.

\[P(A|B) = \frac{P(A,B)}{P(B)} = \frac{P(B|A)P(A)}{P(B,C) + P(B,D) + ... + P(B,Z)}\]

$\sum$ 을 사용해 정리하면 아래와 같다.

\[P(A|B) = \frac{P(B|A)P(A)}{\sum_x P(B,x)} = \frac{P(B|A)P(A)}{\sum_x P(B|x)P(x)}\]

예제) 야구게임

비가 올 확률 ${4 \over 10} = P(A)$
비가 오고 야구팀이 이길 확률 ${6 \over 10} = P(B A)$
비가 안오고 야구팀이 이길 확률 ${3 \over 10} = P(B A^C)$

위와 같은 전제를 알 고 있을 때 $P(A|B)=?$ (야구팀이 이겼다면 비가 왔을 확률은?)

일단 야구팀이 이겼다는 전제가 필요하기에 분모에 야구팀이 이기는 확률을 적용한다.
$P(A)P(B|A) + P(A^c)P(B|A^c) = {4\over10} \times {6\over10} + {6\over10} \times {3\over10}$

비가 오고 야구팀이 이기는 확률 + 비가 안오고 야구팀이 이기는 확률

분자로는 야구팀이 이기는 전제하에 비가오는 확률을 적용 $P(A)P(B|A) = {4\over10} \times {6\over10}$

최종적으로 아래와 같은 식이 된다.

\[{4\over10} \times {6\over10} \over {4\over10} \times {6\over10} + {6\over10} \times {3\over10}\]

정리하면 아래와 같다.
$P(A|B) = {P(A , B) \over P(B)} = {P(A)P(B|A) \over P(B)} = {P(A)P(B|A) \over P(A)P(B|A) + P(A^c)P(B|A^c)}$

야구게임 예제에선 $B$가 일어날 모든 상황이 단 2가지

비가온다 $P(A)$
비가오지않는다 $P(A^c)$

때문에 분모가 그렇게 길지 않다.

부록 - 순열과 조합

순열(Permutation)

$[A, B, C, D, E]$ 배열중 n개를 선택, 나열

\[_nP_r = \frac{n!}{(n-r)!}\]

$ n=5, r=3 $ 일 경우

\[_5P_3 = \frac{5!}{(5-3)} = 5 \times 4 \times 3\]

원순열

$[A, B, C, D, E]$ 에서 n개를 뽑아 원형연결리스트에 나열

\[\frac{_nP_r}{r} = \frac{1}{r} \frac{n!}{(n-r)!}\]

5개를 뽑을경우 $ ABCDE=BCDEA=CDEAB=DEABC=EABCD $
위 5가지 조합은 모두 하나의 조합으로 본다.

만약 모든 원소를 모두 선택하여 원순열을 만들경우 개수는 $(n-1)!$ 이다.

중복순열(permutation with repetition)

$[A, B, C, D, E]$ 에서 n개 뽑아 중복해서 뽑고 나열

\[_n\Pi_r = n^r\]

$n=5, r=3$ 일 경우

\[_5\Pi_3 = 5^3\]

조합(Combination)

$[A, B, C, D, E]$ 배열중 3개를 선택했을때 나올 수 있는 조합의 수

순서가 없는 순열이라 할 수 있다.

\[_nC_r = \frac{n!}{(n-r)!r!}\]

$ n=5, r=3 $ 일 경우

\[_5C_3 = \frac{5!}{2!\times 3!} = \frac{5 \times 4 \times 3}{3!}\]

반대로 생각해서 선택하지 않을 2개를 고르는것과 같다 할 수 있다.

\[_5C_3 = _5C_{5-3} = {5 \times 4 \over 2!}\]

중복조합(Homogeneous monomials: 동차단항식)

$[A, B, C, D, E]$ 배열중 3개를 중복하여 선택했을때 나올 수 있는 조합의 수

\[_nH_r = _{n+r-1}C_r\]