내부점 방법(Interior-point method)
KKT 를 변형한 알고리즘
Convex 문제에서 미분은 Local Minimum 이 되기위한 필요조건이였다.
하지만 equality constraint functions 정의되어 있다면
최적화 지점이 꼭 미분계수 0이 아니더라도 최저값이 될 수 있다.
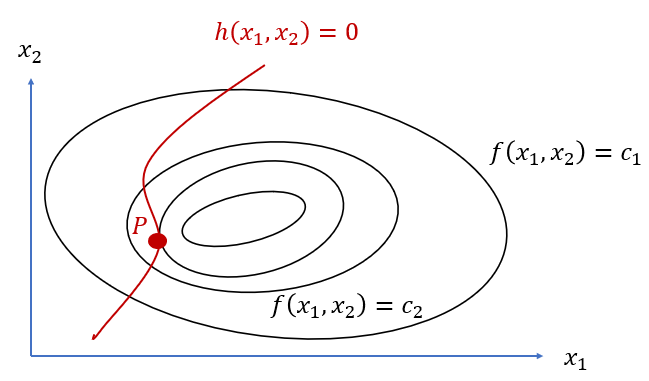
다음과 같이 등고선을 나타내는 3차원 그래프를 위에서 바라보았을 때
$h(x_1, x_2) = 0$ 인 평면이 있을 때 가장 값이 낮은 등고선 $c$ 를 구하는 문제에서
두 함수의 접선이 일치할때, 즉 법선벡터가 수평일 때의 $(x_1, x_2)$ 가 optimul solution 이라 할 수 있다.
이렇게 equality constraint functions 이 존재할 때 최적화는 라그랑주 함수를 사용한다.
equality constraint functions 가 $h(x)$ 하나뿐이라고 가정하고 진행할 때
두 함수의 법선택터가 동일한 수평임으로 아래 조건들을 만족해야 한다.
\[\begin{cases} \nabla f + \lambda \nabla h = 0 \\ h(\vec{x}) = 0 \end{cases}\]조건식 $h(x)$ 은 feasible 결과값이 0이었음으로
이것이 equality contranint function 이 있을 때 Local Minimum 을 뜻하는 필요조건이라 할 수 있다.
이런 규칙아래에서만 발생하는 필요조건을 Regularity conditions(규칙성 조건), Constraint Qualification(조건 제약) 이라 한다.
예제
\[\begin{cases} \min & \|x\|_2^2 = x^Tx \\ \mathrm{s.t} & Z = Ax \end{cases}\]위와같은 equality constraint functions 에서 $\vec{x}$ 의 L2 norm 을 가장 작게 만들 때
\[L = x^Tx + \lambda (Z - Ax)\]$Z - Ax = 0$ 임으로 아래와 같이 라그랑주 함수 $L$ 구성
여기서 $Z - Ax$ 의 차원을 높여 하나의 constraint functions 이 아닌 여러개의 constraint functions 으로 나타낼 수 있다.
$\lambda$ 도 하나의 실수가 아닌 벡터로 표현,
행렬을 사용하면 단순하게 복수게의 constraint functions 을 가진 라그랑주 함수를 구성할 수 있다.
이제 $x$ 에 대해 편미분을 진행하면
\[\begin{aligned} \frac{\partial L}{\partial x} &= 0 \\ x^Tx + x^Tx - \lambda^TAx &= 0 \\ (2x^T - \lambda^TA)x &= 0 \\ \end{aligned}\] \[\begin{aligned} 2x^T &= \lambda^TA \\ x^T &= \frac{1}{2} \lambda^TA \\ x &= \frac{1}{2} A^T \lambda \\ \end{aligned}\]구한 $x$ 를 $\mathrm{s.t}$ 함수에 대입
\[Z = A \frac{1}{2}A^T\lambda\] \[Z = \frac{1}{2}AA^T\lambda\] \[\lambda = 2(AA^T)^{-1}Z\]사실상 $\frac{\partial L}{\partial \lambda}$ 에 대해 $x$ 를 대입한것과 동일함
구한 람다식을 다시 $x$ 에 대입
\[x = \frac{1}{2} A^T 2(AA^T)^{-1}Z\] \[x = A^T(AA^T)^{-1}Z\]출력된 $x$ 가 $x^$ 이다.
이렇듯 constraint functions 이 존재할 경우 라그랑주 함수를 사용하면
$x^$ 을 수식을 통해 한번에 찾아갈 수 있다.
KKT conditions
KKT(Karush–Kuhn–Tucker conditions) conditions
inequality condition function이 존재할 때 최적화 하기 위한 방법
식은 아래와 같다.
\[L(x, \lambda, \mu) = f(x) + \sum_i \lambda_i h_i(x) + \sum_i \mu_i g_i(x)\]만약 condition function 이 아래와 같이 2개 존재한다 예를들면
라그랑주 함수로 아래와 같이 표현할 수 있으며
\[L(x, \lambda, \mu) = f(x) + \lambda h(x) + \mu g(x)\]아래와 같은 필요조건을 만족해야 Local Minimum 이라 할 수 있는데
Stationarity: 정상성 Complementary slackness: 보완적 느슨함 Dual feasibility: 이중 타당성 Primal feasibility: 원초적 타당성
이를 KKT Conditions 라 한다.
Convex 문제에 한하여 KKT Condition 을 만족하는 $\lambda, \mu$ 를 찾으면 $x^*$ 을 찾을 수 있다.
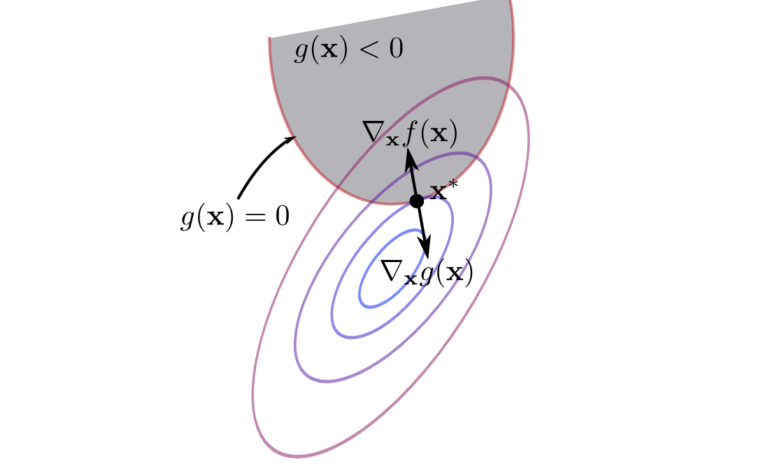
Primal feasibility 중 $g(x) \le 0$ 이기에 $g(x)$ 역시 작을수록 좋은 조건을 가지게 된다는 뜻이고
위의 등고선 그래프를 기반으로 기하학적으로 보면 $f(x), g(x)$ 의 기울기 벡터 $\nabla f(x), \nabla g(x)$ 모두 0에 가까워지면서,
기울기벡터 두개가 수평이면서 반대 방향을 바라보고 있는 교착상태에 직면하는 순간을
줄어들수 있을 만큼 줄어든 상태라 할 수 있다.
그 순간이 (1) Stationarity 조건이다.
등고선 그래프로 봤을때 작은 $f(x)$ 중 기울기벡터 두개가 수평이면서 반대 방향을 바라보고 있는 교착상태라 할 수 있다.
이러한 이유로 (3) Dual feasibility 역시 항상 양수가 되어야 한다.
(1) 조건에 따라 $f’(x)$ 방향과 $\mu g’(x)$ 방향은 서로 반대방향이어야 하는데 음수일경우 방향이 역전되어버림으로 음수가 될 수 없다.
(2) Complementary slackness 을 정리하면 아래와 같다.
- $g(x^) = 0$ 는 경계면에 $x^$ 존재
- $g(x^) \le 0$ 는 경계안에 $x^$ 존재
만약 경계안에 $x^$ 가 있다면 이 때의 제약조건을 보완 제약(slack constraints) 이라함
이 경우는 $g(x)$ 가 $x^$ 를 계산하는데 아무런 영향을 주지 않기때문에 대한 $\mu = 0$ 으로 주어진다.
다음 그림처럼 빨간색 점이 $x^*$ 이라면 파랑색 영역을 뜻하는 $g(x)$ 는 없는것이나 마찬가지
만약 경계선에 $x^$ 가 있다면 이 때의 제약조건을 바운딩 제약(bounding constraints) 이라함
이 경우는 등식 제약조건과 다를 바 없고 $g(x)=0$ 임으로 $\mu g(x^) = 0$ 이다.
이 두 경우를 합치면 (2) complementary slackness 조건이 성립한다.
예제
\[\begin{cases} \min & f(x,y) = x^2+y^2 \\ \mathrm{s.t} & h(x,y) = x+2y=4 \\ & g_1(x,y) = x^2+y^2 \le 5 \\ & g_2(x,y) = x \ge 0 \\ & g_3(x,y) = y \ge 0 \end{cases}\]
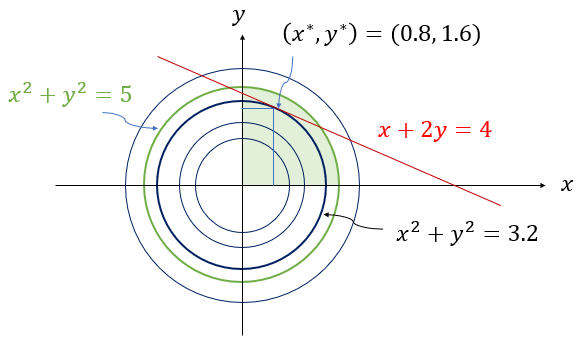
$g_1(x,y), g_2(x,y), g_3(x,y)$ 만족하는 초록색, 그리고 붉은선 위에 있는 영역(Primal feasibility)에서 optimal solution 을 구해야 한다.
이를 위해 KKT Condition 형식으로 문제를 변경
조건에 따른 라그랑주 함수는 아래와 같다.
\[L(x, y, \mu_1, \mu_2, \mu_3, \lambda) = \\ (x^2 + y^2) +\lambda (x+2y-4) + \mu_1 (x^2+y^2-5) + \mu_2(-x) + \mu_3 (-y)\]KKT Condition 조건에 따라 아래와 같이 정리
(1) Stationarity
\[\frac{\partial L}{\partial x} =2x+2x\mu_1-\mu_2+\lambda=0\] \[\frac{\partial L}{\partial y} =2y+2y\mu_1-\mu_3+2\lambda=0\](2) Complementary slackness
\[\mu_1 (x^2+y^2-5) = 0\] \[\mu_2 x = 0\] \[\mu_3 y = 0\](3) Dual feasibility
\[\mu_1, \mu_2, \mu_3 \ge 0\](4) Primal feasibility
\[x^2+y^2-5 \le 0\] \[-x \le 0\] \[-y \le 0\] \[x+2y-4=0\](2) Complementary slackness 에서 모든 $\mu_i \ne 0$ 부터 모든 $\mu_i = 0$ 까지의 경우의 수를 대입하여 $x, y$ 를 구한 후 $x, y$ 가 (4) Primal feasibility 조건을 만족하면서 구하고자 했던 $f(x,y)$ 의 결과값이 가장 작은 $x, y$ 를 구하면 된다.
정답은 아래와 같다.
\[x^*=0.8, \ y^*=1.6\] \[f(x^*, y^* ) = (x^*)^2+(y^*)^2 =3.2\]라그랑주 Duality
inequality condition function 를 가지고 있는 문제에서 KKT Condition 을 이용하였다.
$\min f(x)$ 를 구하는 문제를 primal-problem
$x^$ 를 pirmal-optimal
$f(x^)$ 를 primal-optimal-value 라 한다.
KKT Condition 의 primal-problem 아닌 dual-problem 문제로 만들어 최적화 하는 방법을 소개한다.
라그랑주 함수 $L$ 자체를 minimize 하는 라그랑주 듀얼함수 $d(\mu, \lambda)$ 를 구하고
maximize 할 수 있는 $\mu, \lambda$ 를 구하는 것이 dual-problem 문제해결의 핵심
기존의 condition function 의 교차되는 경계점을 찾아다니기 위해 라그랑주 함수 $L$ 을 $x$ 로 편미분하는 것과는 다른 방식이다.
듀얼함수 $d(\mu,\lambda)$ 는 라그랑지 함수 $L$ 을 제약조건 없이 minimize 한것
라그랑주 함수 $L$ 은 목적식 $f(x)$ 에서 $\mu g(x) \le 0$ 를 더한 값이기에
모든 $x$ 에 대해서 이런 특징때문에 아래 같은 관계가 만족한다.
\[d(\mu,\lambda) \le L(x,\mu,\lambda) \le f(x)\]primal problem 인 $\min f(x)$ 의 primal optimal value 을 $P^$
dual problem 인 $\max d(\mu,\lambda)$ 의 dual optimal value 을 $D^$
$ D^* \le P^* $ 관계를 weak duality
$ D^* = P^* $ 관계를 strong duality
$P^* , D^*$ 차이를 duality gap
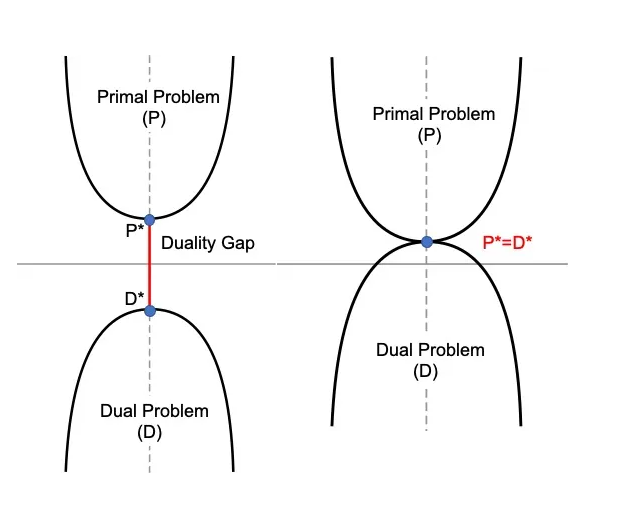
그림처럼 duality gap 이 없는
$d(\mu,\lambda) = f(x)$ 를 만족하는 feasible $x, \lambda, \mu $가 optimal value 가 된다.
위 조건을 만족하는 $\mu, \lambda$ 를 찾으면 된다.
예제
\[\begin{cases} \min & f(x) = x_1 + x_2 \\ \mathrm{s.t} & g(x) = x_1^2 + x_2^2 - 1 \le 0 \end{cases}\] \[\begin{aligned} d(\mu, \lambda) &= \min_x L(x, \mu, \lambda) \\ &= \min_x (x_1 + x_2 + \mu (x_1^2 + x_2^2 - 1)) \end{aligned}\]min 값을 구하기 위해 편미분
\[\frac{\partial L}{\partial x_1} = 1 + \mu 2x_1 =0\] \[\frac{\partial L}{\partial x_2} = 1 + \mu 2x_2 =0\] \[x_1 = x_2 = -\frac{1}{2\mu}\]구한 $x_1, x_2$ 를 위의 라그랑주 함수 $L$ 에 대입
\[\begin{aligned} & x_1 + x_2 + \mu (x_1^2 + x_2^2 - 1) \\ &= -\frac{1}{2\mu} - \frac{1}{2\mu} + \mu(\frac{1}{4\mu^2}+\frac{1}{4\mu^2}-1) \\ &= \frac{1}{\mu} + \frac{1}{2\mu} - \mu \\ &= -\frac{1}{2\mu} - \mu \end{aligned}\]최종적으로 라그랑주 듀얼함수는 아래와 같다.
\[d(\mu, \lambda) = \min (-\frac{1}{2\mu} - \mu)\]아래 그림과 같은 그래프가 그려지는데
$\mu$ 는 항상 양수임으로 왼쪽의 convex 형태의 그래프는 무시한다.
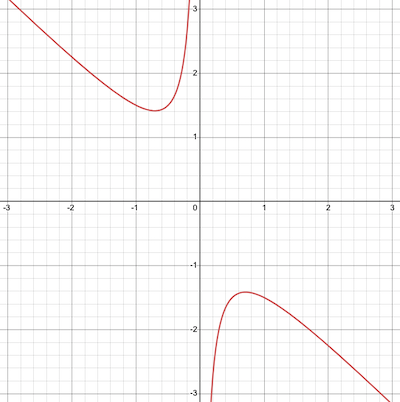
듀얼 문제를 해결하는 방법이 $\max d(\mu, \lambda)$ 임으로
마찬가지로 미분 0 되는 지점을 구해 Local Maximize 을 구하면 된다.
$d(\mu, \lambda)$ 에서 $\mu$ 에 대해 편미분
\[\frac{\partial d(\mu, \lambda)}{\partial \mu}= \frac{1}{2\mu^2} -1 = 0 \\ \mu = \plusmn \frac{\sqrt{2}}{2}\]하지만 $\mu \ge 0$ 임으로 \(\mu = \frac{\sqrt{2}}{2} \\ x_1=x_2 = -\frac{2}{\sqrt{2}}\)