Gradient Decent Method
가까운 Local Minimum 지점을 찾아주는 solution
Convex 함수가 아닐 경우 초기에 어떤값을 주는지(시작점)에 따라 solution 값이 달라지기 때문에
initial 값이 매우 중요하지만 Local Minimum 찾기 좋은 solution
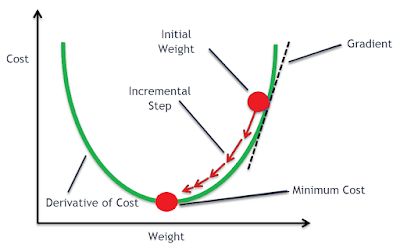
다음 그림과 같이 미분계수를 사용해 하강 방향을 결정하고
Initial: 랜덤으로 지정하는 시작 위치
Gradient: 방향, 위 그림처럼 미분계수를 사용함
Step Size: 방향으로 얼마나 이동할 건지의 실수값
\[x_{k+1} = x_k - a \frac{\partial f}{\partial x}\]미분계수가 0에 가까워져 $x_{k+1}$ 와 $x_k$ 가 거의 변화가 없다면 Local Minimum 을 찾았다 할 수 있다.
예제
\[Z = x + n\]Newton’s method
경사하강법 최소값을 향한 방향을 계산하는데 1차 미분을 사용하는 반면 뉴턴방법은 2차 미분을 사용한다.
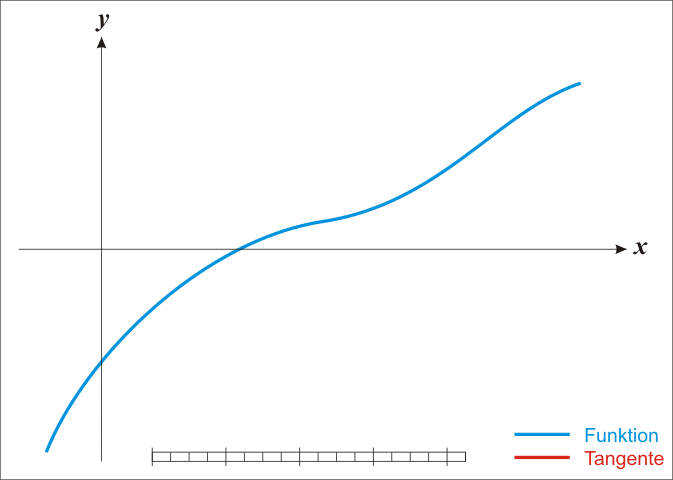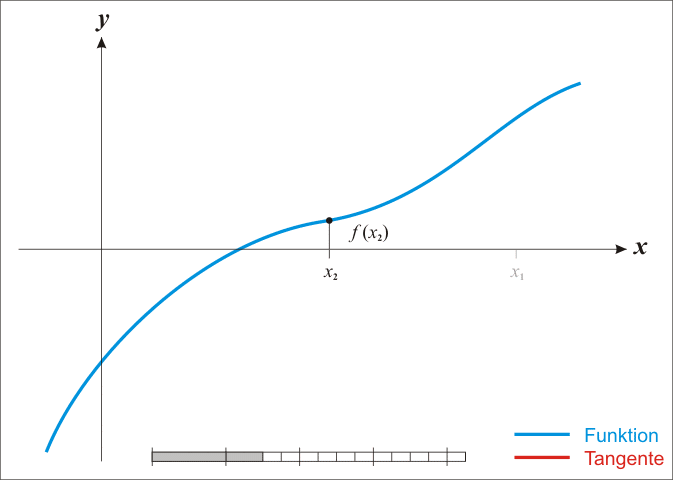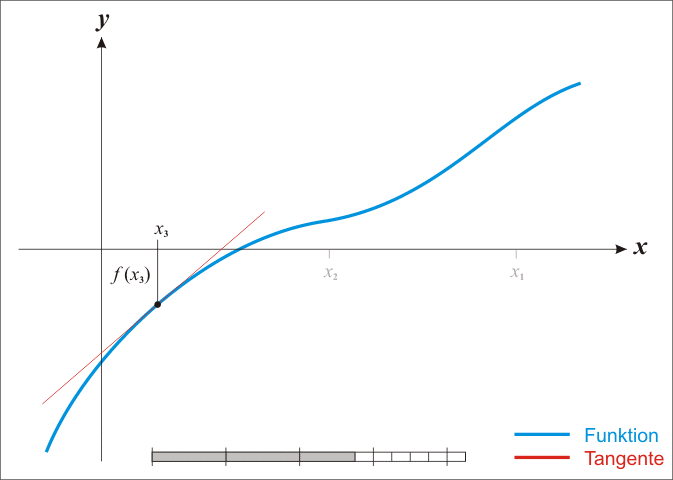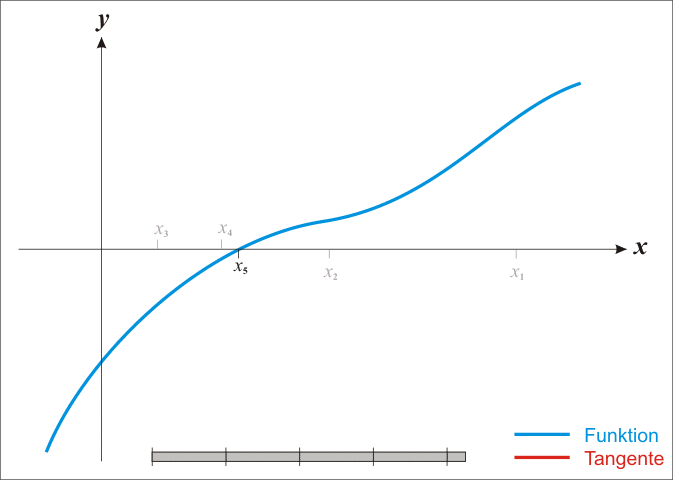
아래 그림처럼 이미 미분처리가 완료된 그래프(기울기 그래프) $g(x)$ 에서 0 이 되는 지점을 찾으면
원래 함수 $f(x)$ 에서 기울기가 0이 되는 $x^*$ 을 찾았다고 할 수 있다.
출처: https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=tlaja&logNo=220731745142
경사하강법과 다르게 step size 를 지정할 필요도 없고 좀더 빠른 속도로 $x^*$ 을 찾는다.
위 그래프는 이미 미분된 그래프이니 프라임을 하나 더 붙인다.
해당식은 일차 테일러 급수
Least-Squares Solution (최소제곱해)
quasi-Newton methods
quasi: 콰지, 준하는
미분비용이 너무 많이들어 만들어진 방법으로
순간 기울기(미분) 대신 $x_k$ 와 $x_{k+1}$ 사이의 기울기를 사용한다다
이 기울기를 B_k 로 표기하고 식도 아래처럼 간단하게 표기
\[B_k = \frac{y_{k-1}}{S_{k-1}}\]업데이트 수식은 아래와 같다.
\[x_{k+1} = x_k - B_k f'(x_k)\]