개요
https://www.youtube.com/watch?v=lmD9p6J_-TA 라그랑주 승수는 식으로 주어진 영역에서 추가적으로 제약된(constraint) 다변수 실함수의 임계점(critical point)을 구하는 데에 사용되는 판별법이다.
시각적으로 이해하기위해 이변수 함수를 기반으로 3차원 그래프로 생각해보자.
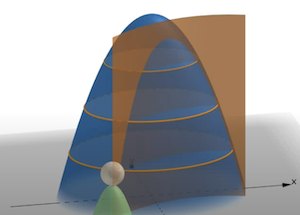
\[f(x,y) = 4 - x^2 - 2y^2 \\\]정점 4를 기준으로 등고가 있는 모형이 그려진다.

이때 위 $g(x,y)$ 의 제약조건(함수식=0)을 설정해서 그림처럼 평면으로 만들어 잘랐을 때
수직으로 보면 아래 그림과 같다.
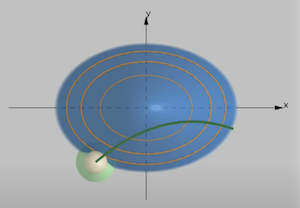
이때 $f(x,y)$ 와 $g(x,y)$ 가 접하는 접선(모든 $x,y$)을 $f(x,y)$ 에 대입했을 때 가장 높은값을 가지는 $(x,y)$ 를 구할때
\[\begin{cases} \max & f(x, y) \\ \mathrm{s.t} & g(x,y) = 0 \end{cases}\]라그랑주 승수법을 사용하면 구할 수 있다.
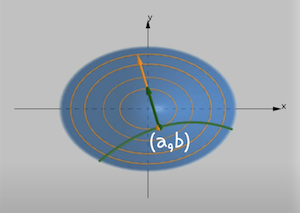
다음과 같이 가장 높은 접점을 $(a,b)$ 로 가정한다면
$f(a,b)$ 는 $g(a,b)$ 와 접하는 가장 작은 타원을 그리게 된다.
접한다는 것은 $f(a,b), g(a,b)$ 모두 같은 기울기의 접선을 가진다는 뜻이다.
gradient vector(구배벡터)
같은기울기의 접선은 다르게 말하면 접점으로부터 수직이 되는 gradient vector 의 방향이 같다는 뜻
함수로부터 gradient vector 를 구하는 수식은 다음과 같다.
\[\nabla f = \left( \frac{\sigma f}{\sigma x}, \frac{\sigma f}{\sigma y} \right)\]두 함수식이 다르기에 두 gradient vector 의 스칼라 또한 다르다.
따라서 위의 $f(a,b), g(a,b)$ 의 gradient vector 관계식을 아래처럼 표현할 수 있는데
\[\nabla f(a,b) = \lambda \nabla g(a,b)\]이때 $\lambda$ 를 라그랑주 승수 라 부른다.
라그랑주 승수법(Lagrange multiplier method)
위 예제에서 함수 $g(x,y)=0$ 이 되도록 제약조건을 설정했다.
이런 특성을 기반으로 라그랑주 승수식 $L(x, y, \lambda)$ 을 아래처럼 작성할 수 있다.
\[L(x, y, \lambda) = f(x,y) - \lambda(g(x,y) -c)\]이때 상수 $c$ 는 제약조건
만약 제약조건인 함수$g$ 가 1개가 아닌 $n$ 개인 경우는 아래와 같은 식을 사용
\[L(x,y,\lambda_1,\lambda_2,\cdots,\lambda_n) = f(x,y) - \sum_{i=1}^n \lambda_i(g(x,y) -c_i)\]함수 $L$ 두 함수 $f,g$ 의 구배백터간의 뺄샘으로 만들기 위해
$L$에 대하여 $x$ 와 $y$ 를 편미분하면 모두 0 이 나오는 조건식을 만든다.
\[\frac{\partial L}{\partial x}=0, \quad \frac{\partial L}{\partial y}=0\]둘의 접합지점이 되려면 뺄샘의 결과가 영백터이여야 함으로
예제1
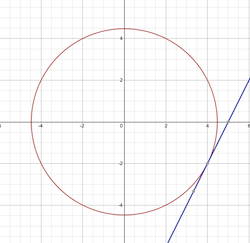
\[\begin{cases} & f(x,y)=x+y=c \\ \mathrm{s.t}& g(x,y)=x^2+y^2=1 \end{cases}\]원의 방정식이 제약조건이고
직선의 방정식이 구해야할 값이다.
두 접선의 gradient vector 가 일치하는 부분이 $c$ 의 최대, 최소값이다.
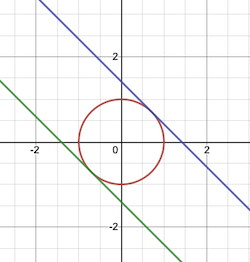
즉 원에 접하는 조건이기에 $c$ 의 최대 최소는 원에 접하는 직선의 y절편일 것이다.
편미분을 통해 각각의 기울기 백터를 구하면 \(\nabla f = (1,1) \\ \nabla g = (2x,2y)\)
$\nabla f = \lambda \nabla g$ 식에 대입하면 아래와 같다.
\[(1,1) = \lambda(2x, 2y) \\ (1,1) = (\lambda 2x, \lambda 2y) \\ x=\frac{1}{2\lambda}, y=\frac{1}{2\lambda}\]함수 $g,f$ 의 $x, y$ 에 $\lambda$ 를 적용해 구하면 $\lambda = \pm\frac{1}{\sqrt{2}}$ 가 되고
$x=\frac{1}{2\lambda}, y=\frac{1}{2\lambda}$ 임으로 그대로 $x+y=c$ 에 대입하면 $c=\pm\sqrt{2}$ 가 된다.
예제2
$g(x,y)=2x-y-10=0$ 을 만족할 때 $f(x,y) = x^2+y^2 = c$ 의 최소값을 구하여라,
라그랑주 승수식을 사용해 표현하면
\[L(x, y, \lambda) = f(x,y) - \lambda(g(x,y) -c) \\ L(x, y, \lambda) = x^2+y^2 - \lambda(2x-y-10)\] \[\frac{\partial L}{\partial x} = 2x - 2\lambda = 0 \\ \ \\ \frac{\partial L}{\partial y} = 2y + \lambda = 0\] \[x = \lambda, \quad y = -\frac{1}{2}\lambda\]마찬가지로 $g(x,y)$ 에 대한 식에 $\lambda$ 를 지정하면 $\lambda$ 를 구하고
$f(x,y)$ 에 $x, y$ 값을 대입하여 $c$ 를 구한다.
$2x - y = 10$ 그래프와 $x^2 + y^2 = 20$ 그래프는 아래와 같다.