개요
https://convex-optimization-for-all.github.io/contents/chapter01/
최적화 문제(Optimization problems) 란 여러개의 선택가능한 후보 중에서 최적의 해(Optimal value) 를 찾는 문제를 일컫는다
\[\begin{cases} \mathrm{object} & \min f(x) \\ \mathrm{s.t} & h(x) = 0\\ & g(x) \le 0 \end{cases}\]objective function: 목적함수로 cost function 이라 부르기도 함
constraint functions: 제약식으로 inequality, equality 등이 될 수 있음, $\le, \ge$ 는 active inequality constraint functions 이라 부르기도 함
feasible solution: objective function 의 정의역에 있으며 constraint functions 을 만족하는 벡터들
feasible set: feasible solution 들의 집합
optimal solution: feasible set 중 최적의 objective function 를 만드는벡터 $\vec{x}$, $x^*$ 로 표기
극대점, 극소점
Local Maximum, Local Minimum, 함수 특정 지점에서 가장 작은, 가장 큰 값을 가지는 지점
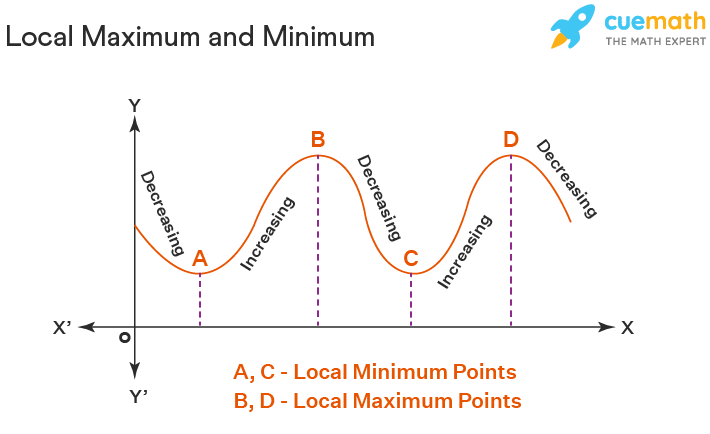
꼭 미분 가능한 지점이 아니더라도 극소점, 극대점이 될 수 있다.
Local Maximum, Local Minimum 중 가장 큰, 가장 작은 지점을 Global Maximum, Global Minimum 이라 함.
Convex Optimization
Convex sets: 컨벡스 조건을 만족하는 벡터들의 집합
$S$(feasible set) 에 포함되는 두 벡터가 아래 조건을 만족하면 Convex 라 할 수 있다.
아래 그림처럼 표현할 수 있다.
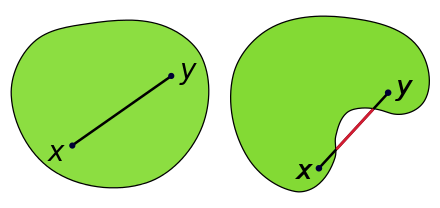
위의 $a\vec{x_1} + (1-a)\vec{x_2}$ 공식은 두 벡터 사이의 직선을 표현함
Convex functions: 볼록 함수, 볼록 함수는 임의의 두 점을 이은 할선이 두 점을 이은 곡선보다 위에 있는 함수.
Concave functions: 오목 함수, 반대로 임의의 두 점을 이은 할선이 두 점을 이은 곡선보다 아래에 있는 함수.
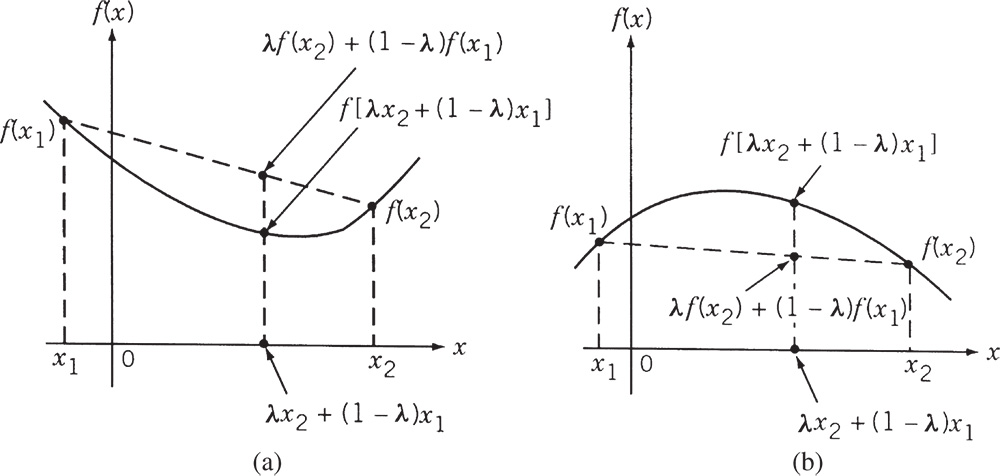
$x_1 ,x_2$ 사이 거리가 1, $\lambda$ 로 내분하였을 때
\[\lambda \in [0,1]\] \[\mathrm{convex} \\ f(\lambda\vec{x_1} + (1 - \lambda) \vec{x_2}) \le \lambda f(\vec{x_1}) + (1-\lambda)f(\vec{x_2})\] \[\mathrm{concave} \\ f(\lambda x_2 + (1-\lambda)x_1) \ge \lambda f(x_2) + (1-\lambda)(fx_1)\]convex, concave 둘다 점 사이를 이었을 때 생기는 직선 식을 확인
Convex 문제에선 Local Minimum 이 Global Minimum
Concave 문제에선 Local Maximum 이 Global Maximum 이다.
대부분의 문제가 Local Minimum 을 구하는 문제이고
Non-Convex 문제를 Convex 문제로 변경할 수만 있다면 Local Minimum 이 해결되기에 최적화에서 자주 사용된다.
전 구간에서 미분 가능한 함수 $f(x)$ 일경우
그리고 전 구간에서 $f’‘(x) > 0$ 일 경우 Convex 함수라 할 수 있다.
그리고 전 구간에서 $f’‘(x) < 0$ 일 경우 Concave 함수라 할 수 있다.