고유백터(Eigen vector) 고유값(Eigen value)
$A \vec{x} = \lambda \vec{x}$
위 공식과 같이 선형봔환된 벡터의 값 = 상수배 벡터의 값이라면 (만족하는 실수 $\lambda$ 가 존재하면)
$\lambda$ 를 행렬 $A$ 의 고유값
$\vec{x}$ 를 행렬 $A$ 의 고유백터라 한다
기하학적으로 행렬을 사용해 벡터 선형변환 했을때 방향이 바뀌지 않고 실수배만큼 늘었을 때
사용하는 개념이 고유값과 고유백터이다.
기하학적으로 보면 아래 그림과 같다.
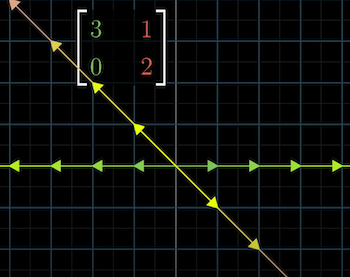
위와 같은 행렬로 선형변환될때 $x$ 축에 해당하는 초록색, 노란색에 해당하는 백터들은 모두 고유백터가 된다.
또한 행렬 $A$ 와 $x$ 의 행렬곱셈 결과값이 $x$ 백터의 차원수와 동일해야 함으로 $A$ 는 정사각행렬이어야 한다.
\[A \vec{x} - \lambda \vec{x} = 0 \\ (A - \lambda I) \vec{x} = 0\] \[(A - \lambda I) \begin{bmatrix} a\\b\\...\\z \end{bmatrix} = \begin{bmatrix} 0 \\0 \\...\\0 \end{bmatrix}\]위 공식으로부터 $\lambda$에 대한 방정식을 이끌어 내야한다.
$\vec{x}$ 는 영백터가 아니기에 $(A - \lambda I)$ 가 영행렬이 출력되야 하고
행렬식을 이용해 $A$ 와 $\lambda$ 의 방정식, 특성 방정식(characteristic equation) 을 유도할 수 있다.
또한 영공간의 정의가 $Ax = 0$ 를 만족하는 $x$ 의 집합 인데
$(A - \lambda I) \vec{x} = 0$ 과 일치한다.
즉 고유백터는 아래 영공간에 해당되는 모든 백터임으로 개수가 무한하다.
단 independent 한 고유벡터중 단위벡터만을 대표로 사용한다.
고유벡터 계산
행렬 $A$ 를 예로들면 아래 행렬식 연산에 따라 $\lambda$ 를 구할 수 있다.
\[A = \begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix}\] \[\det(A - \lambda I) = \det \left( \begin{bmatrix} 3 - \lambda & 1 \\ 0 & 2 - \lambda \end{bmatrix} \right) = 0\] \[(3-\lambda) (2-\lambda) - 1 \cdot 0 = 0 \\ \lambda_1 = 2 \\ \lambda_2 = 3\]그리고 고유벡터는 $A \vec{x} = \lambda\vec{x}$ 임으로 $\lambda = 2$ 일 때 연립방정식으로 고유벡터를 구하면 아래와 같다.
\[\begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 2\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\] \[3x_1 + x_2 = 2x_1 \\ 2x_2 = 2x_2 \\ x_1 = -x_2 \\\]위 조건을 만족하는 모든 벡터값은 모두 고유벡터라 할 수 있다.
고유값 $\lambda = 2$ 임으로 위 조건 벡터들은 행렬 $A$ 로 선형변환시 2배 늘어난다.
$\lambda = 3$ 일 때 연립방정식으로 고유벡터를 구하면 아래와 같다.
\[\begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 3 \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\] \[3x_1 + x_2 = 3x_1 \\ x_2 = 3x_2 \\ x_2 = 0 \\\]위 조건을 만족하는 모든 벡터값은 모두 고유벡터라 할 수 있다.($x_2$ 가 0 인 아무 벡터) 고유값 $\lambda = 3$ 임으로 위 조건 벡터들은 행렬 $A$ 로 선형변환하면 3 배 늘어난다.
고유값 분해(Eigen decomposition)
아래와 같은 고유값, 고유백터를 이미 구했다고 가정했을 때
\[A x_1 = \lambda_1 x_1 \\ A x_2 = \lambda_2 x_2\]두 수식을 합친다.
\[[A x_1, A x_2] = [\lambda_1 x_1 , \lambda_2 x_2]\] \[A[x_1, x_2] = [x_1 , x_2] \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}\]행렬을 아래처럼 치환하고 행렬 A 에 대한 식을 구한다.
\[[x_1, x_2] = V\] \[\begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} = \Lambda\] \[A V = V \Lambda \\ A = V \Lambda V^{-1} \\\]n x n 행렬 $A$ 에서 independent 한 고유값 n 개를 구하여 위와 같은 행렬 수식을 만드는 것이
행렬 A 의 고유값 분해이다
또한 행렬 $A$ 를 대각행렬 $\Lambda$ 로 표현했기 때문에 행렬의 대각화(diagonalization) 라고 하기도 한다.
행렬 $V$ 역시 정사각 행렬, 2차원을 예로들어서 그렇지 n 차원의 n 개의 열벡터의 모음이기에 정사각 행렬이다.
대각화가능행렬(Diagonalizable matrix)
행렬 A 를 대각행렬 $\Lambda$ 로 표기할 수 있기 때문에
고유값 분해를 하는 이유는 사실 대각화를 하귀 위해서라고도 할 수 있다.
모든 행렬이 대각화 할수 있는것은 아니고 위와같이 고유값 분해가 가능한 행렬이 바로 대각화가능행렬이다.
대각행렬은 여거라지 이점이 있다.
아래 그림처럼 100번을 곱해도 단순한 수식으로 표현할 수 있다.
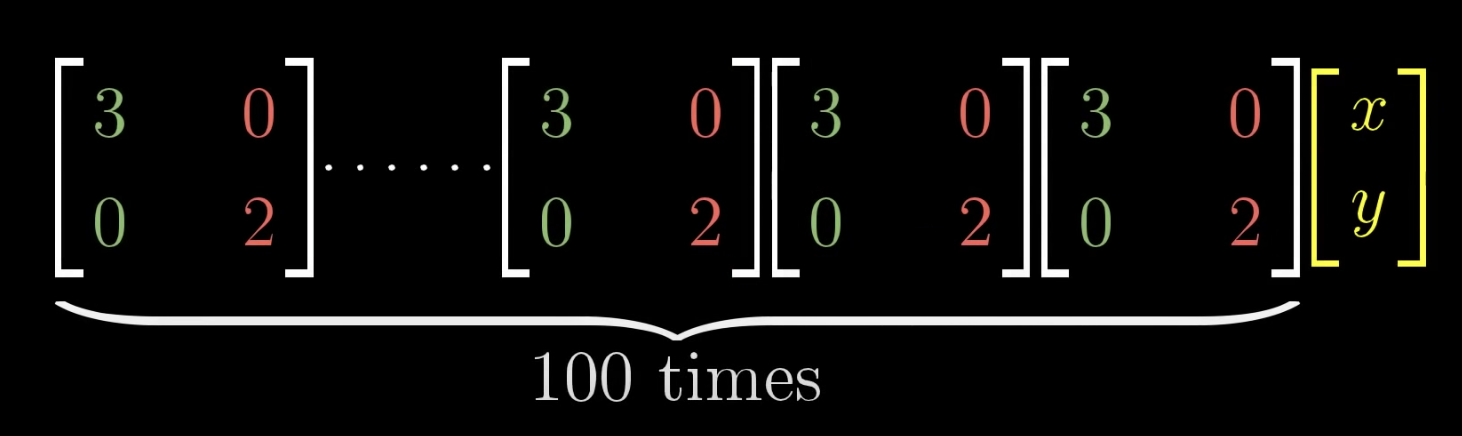
대각행렬의 행렬식과 대각합에 대해서도 아래와 같이 단순하게 표현할 수 있다.
\[\det(A) = \det(V \Lambda V^{-1}) = \det(V)\det(\Lambda)\det(V^{-1}) \\ = \det(\Lambda) = \lambda_1 \lambda_2 \cdots \lambda_n = \Pi^n_{i=1}\lambda_i\] \[tr(A) = \sum^n_{i=1} \lambda_i\]고유백터가 기저백터가 되도록 좌표계를 변경하는것이 고유기저라 할 수 있다.
좌표계를 변경한다는 것은 양옆으로 행렬과 그에 해당하는 역행렬을 곱합으로써 이루어진다.
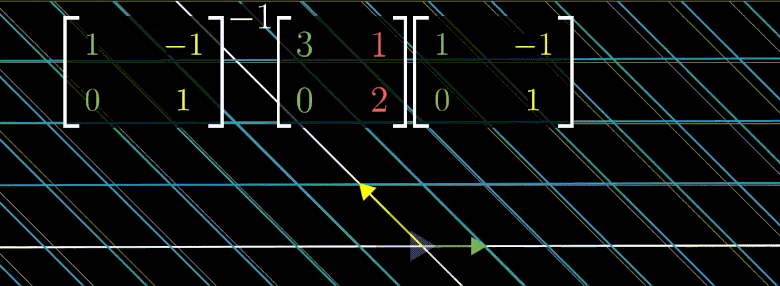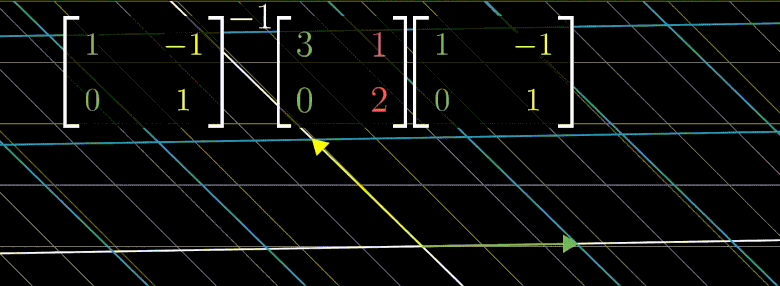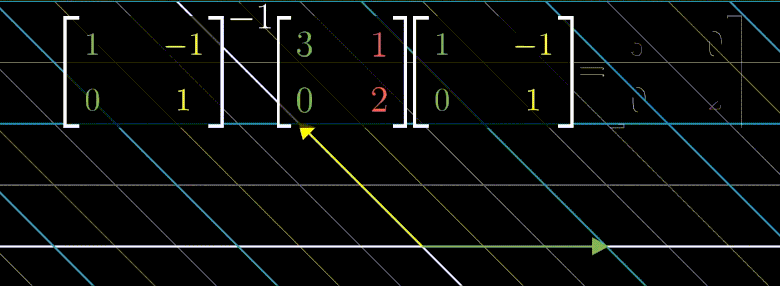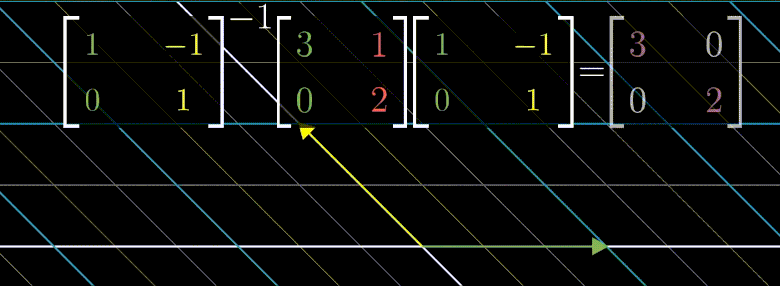
위의 제니퍼 좌표계 변환법을 생각해보자.
위의 연산은 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 의 기저백터로 좌표계를 변환후 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 선형변환을 한것이기에
변환된 좌표계 입장에서 x 축 y 축 기반으로 늘어날 뿐이다.
만약 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}^{100}$ 한 결과를 알고싶다면 고유기저로 변경 후 계산하고 다시 원래 좌표계로 변환하는 것이 더 효율적이다.
대각화를 하는 제일큰 이유는 행렬의 거듭제곱이 매우 편해진다.
행렬 종류의 따른 고유값 특징
행렬이 rotate 의 경우 고유백터는 존재하지 않고 ($\lambda$ 해가 없음)
행렬이 shearing 의 경우 고유값은 한개이상 존재 ($\lambda$ 해가 이상)
대각행렬은 $x, y$ 축 방향으로 shearing 이라 할 수 있으며
해가 1개일 경우 단위행렬의 배수 형태로 정방향 확대, 모든 백터는 고유백터가 되고
해가 2개일 경우 x, y 축에 평행하는 백터는 모두 고유백터가 된다.
전치행렬 $A^T$ 의 고유값은 A 의 고유값과 동일하다.
직교행렬의 경우 $\lambda_i = \pm 1$ 이다.
행렬이 positive semi definite (p.s.d) 일 경우 $\lambda_i \ge 0$ 이다.
대각화 가능 행렬의 고유값의 수는 rank 수와 동일하다.
대칭행렬과 고유값 분해
대칭행렬의 고유값이 특이한 점은 고유벡터들이 서로 직교한다는 점이다.
\[A = A^T\]위 조건을 만족하는것이 대칭행렬
\[A = V \Lambda V^{-1}\] \[A^T = (V^{-1})^T \Lambda V^T\]대칭행렬임으로 $A=A^T$ 가 동일함으로 $V$ 의 관계식을 아래처럼 구성 가능하다.
\[V \Lambda V^{-1} = (V^{-1})^T \Lambda V^T\] \[V = (V^{-1})^T \\ V^{-1} = V^T\]역행렬이 전치행렬인 조건은 직교행렬의 특성이다.
\[A = Q \Lambda Q^T\]직교행렬을 $Q$ 로 나타냄
이런 특징때문에 대칭행렬의 대각화(고유값 분해)를 직교 대각화가능(Orthogonally Diagonalizable) 이라 한다.
\[A = \begin{bmatrix} q_1 & q_2 & q_3 \end{bmatrix} \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T \end{bmatrix}\] \[= \begin{bmatrix} \lambda_1 q_1 & \lambda_2 q_2 & \lambda_3q_3 \end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T \end{bmatrix}\] \[= \lambda_1 q_1 q_1^T + \lambda_2 q_2 q_2^T + \lambda_3q_3 q_3^T\]A를 위와 같이 표현한 것을 A의 스펙트럼 분해(spectral decomposition) 라 한다.
여기서 $q_n q_n^T$ 은