선형변환 (Linear transformation)
출처: https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
선형변환은 선형 결합을 보존하는, 두 벡터 공간 사이의 함수이다
비선형 변환

선형변환

선형변환은 변환 이후에 격자가 직선을 유지하며 평행, 균등하게 변화, 원점을 유지하는 것
위같은 특징때문에 선형변환은 선형사상(Linear mapping) 이라고도 한다.
이중 유명항 변환방법은 3가지 shearing(늘리기), rotation(회전), permutation(반전)
선형결합(linear combination)
백터 $\vec{v_1}, \vec{v_2}, \vec{v_3}$ 가 있을 때 상수배한 후 더한 것을 선형결합이라 할 수 있다.
\[\vec{v_4} = a_1\vec{v_1} + a_2\vec{v_2} + a_3\vec{v_3}\]이 백터들의 상수배(linear) 하고 결합(combination) 해서 만들어지는 새로운 백터를 선형결합의 결과 백터이다.
선형독립(linear independent)
2차원 평면에서 벡터는 서로 평행하지만 않으면 선형결합을 통해 2차원평면 전체를 span 으로 가질 수 있는데 이경우를 선형독립이라 한다.
수학적 정의는 아래와 같다.
\[a_1\vec{v_1} + a_2\vec{v_2} + \cdots + a_n\vec{v_n} = 0\]만약 벡터들의 선형결합을 0으로 표현할 수 있을때 모든 $a_n=0$ 이 되어야만 하는 상황이라면 선형독립이라 할 수 있다.
2차원 평면에서 벡터가 서로 평행해 span 이 하나의 직선일 경우 선형독립이 아니다.
선형독립 하는 벡터의 수가 곧 해당 벡터들을 선형결합하여 표현할 수 있는 차원의 수이다.
기저백터(basis vector) 단위백터(unit Vactors)
기저벡터(basis vector) 는 span 하여 2차원 평면 전체를 표현할 수 있는 벡터라 할 수 있다.
그중에서도 길이 1을 가지는 벡터를 단위벡터(unit Vactors) 라 한다.
예로 아래의 $i, j$ 를 들 수 있다.
$i = \begin{bmatrix} 1\0 \end{bmatrix}, j=\begin{bmatrix} 0\1 \end{bmatrix}$
위의 그림의 경우 단위백터 $i, j$ 를 사용해 $\vec{v}$ 를 만들었다.
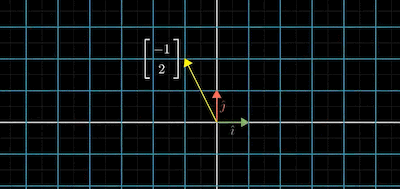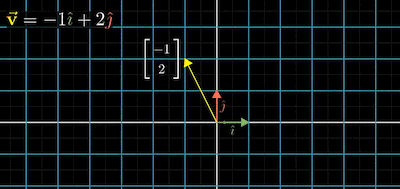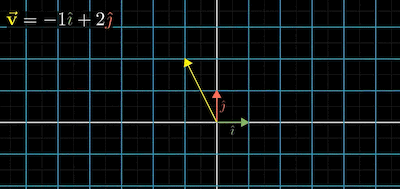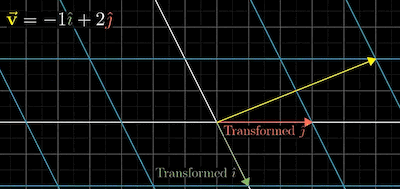
\[\vec{v} = -1\begin{bmatrix} 1\\0 \end{bmatrix} + 2\begin{bmatrix} 0\\1 \end{bmatrix} = \begin{bmatrix} -1\\2 \end{bmatrix}\]위 단위백터를 아래처럼 변경한다면
\[i = \begin{bmatrix} 1\\-2 \end{bmatrix}, \ j=\begin{bmatrix} 3\\0 \end{bmatrix}\]표현가능한 기저가 변경되고 모든 좌표계의 객체들이 선형변환된다.
\[\vec{v}_{out} = -1\begin{bmatrix} 1\\-2 \end{bmatrix} +2\begin{bmatrix} 3\\0 \end{bmatrix} =\begin{bmatrix} 5\\2 \end{bmatrix}\]기저의 객체였던 $\vec{v}$ 또한 변경된다.
단위백터를 변경함으로 기저를 변화시키는데, 단위백터의 변경은 곧 행렬을 뜻하고
백터와 행렬의 곱은 기저의 변경에 따른 백터의 선형변환이라 할 수 있다.
위의 기저벡터변환과 아래의 행렬간 곱셈의 결과가 동일하다.
\[A \vec{v} = \begin{bmatrix} 1&3\\-2&0 \end{bmatrix} \begin{bmatrix} -1\\2 \end{bmatrix} = \begin{bmatrix} 5\\2 \end{bmatrix}\]지금까지
shearing변환에 대해 알아보았다.
값을 대입하여 어떤 백터인던지 행렬에 의한 선형변환을 할 수 있음
선형변환의 합성(행렬의 합성)
행렬는 일종의 함수, 백터는 해당 함수의 입력값으로 보고 계산할 수 있다.
$f(\vec{x})$
한번의 선형변화을 거치고 또 다시 다른 선형변환을 거칠경우
두행렬을 하나의 함수로 합칠 수 있다.
예를들어 왼쪽으로 90° raotation 후 오른쪽으로 shearing 할 경우 기저를 표현하는 단위백터는 아래와 같다.
헹렬 2개를 합치는 과정, 두 행렬의 행렬간 곱셈 으로 생성되었는데
아래 그림과 같다.
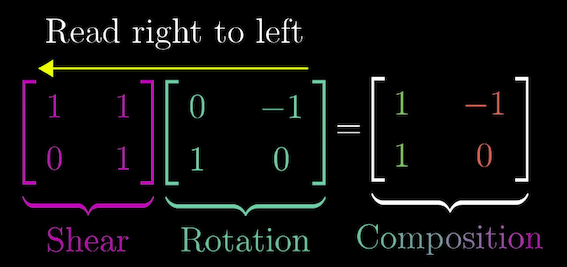
오른쪽부터 먼저 진행된다. 행렬 연산 순서에 따라 결과가 달라짐으로 주의
직관적으로 이해하려면 가장 오른쪽 행렬을 이미 변환된 2개의 단위백터라 생각하고 연산을 진행 했다 보면 된다.
선형대수에서 행렬식
행렬(함수)의 행렬식은 그래프에서 얼마나 물체를 확장시키는지를 알 수 있다.
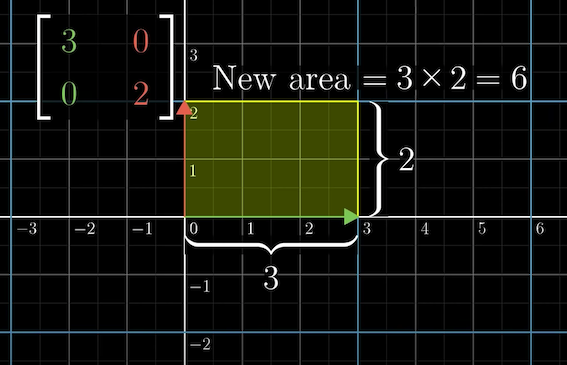
행렬식을 구함으로 특정 area 가 몇배가 될지 알수있게 된다.
만약 행렬식이 0이 된다면 공간이 찌그러지면서 2차원의 경우 1차원 선이 된다.
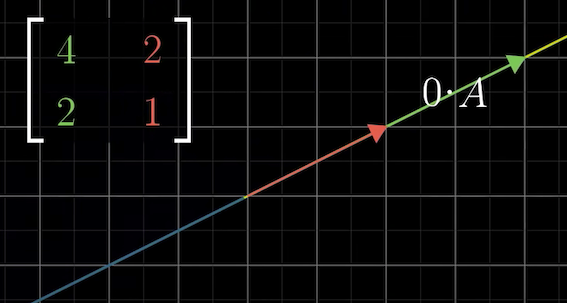
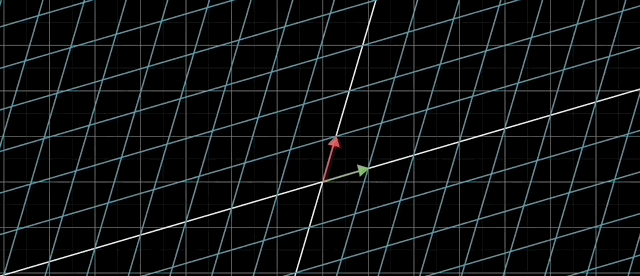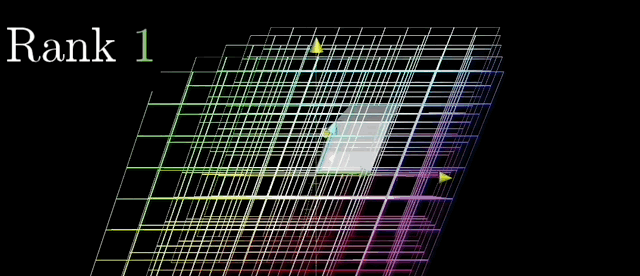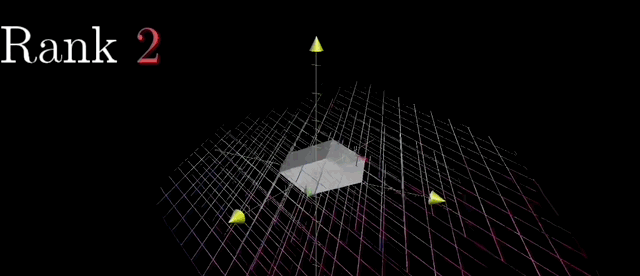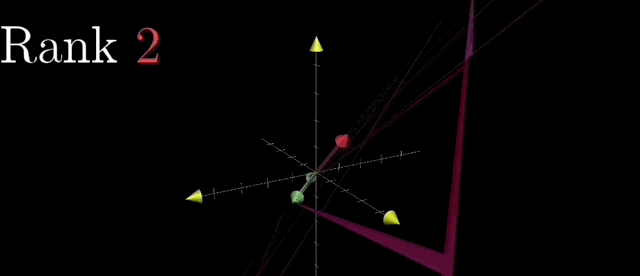
행렬식은 음수가 출력될수 있는데 이는 방향을 뜻한다.
$\hat{i}$(초록) 는 항상 $\hat{j}$(빨강) 보다 오른쪽에 위치한다.
음수 행렬식을 적용하게 된다면 역으로 $\hat{i}$ 오른쪽에 $\hat{j}$ 이 위치하게 된다.
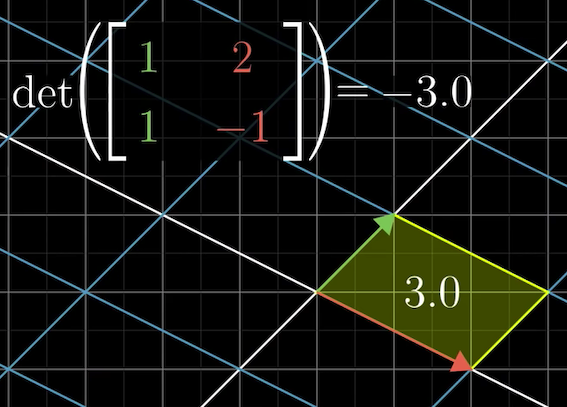
행렬식의 기하학적 의미
사실 행렬은 열백터 혹은 행백터로 이루어진 백터의 집합이라 할 수 있다.
행백터 $v1=\begin{bmatrix} a&b \end{bmatrix}$
행백터 $v2=\begin{bmatrix} c&d \end{bmatrix}$
$v1$의 열백터 $v3=\begin{bmatrix} a\b \end{bmatrix}$
$v2$의 열백터 $v4=\begin{bmatrix} c\d \end{bmatrix}$
행백터의 집합$A=\begin{bmatrix} a&b \ c&d \end{bmatrix}$
열백터의 집합$A^T=\begin{bmatrix} a&c \ b&d \end{bmatrix}$
행백터이건 열백터이건 두 백터를 사용해 행력식을 구해봤자 같은 값의 평행사변형 넓이가 나온다. $|A| = |A^T|$
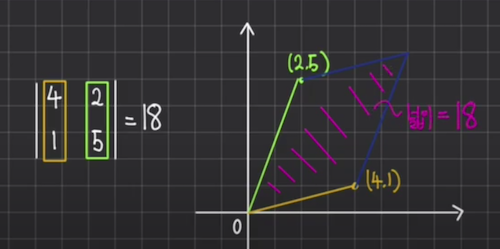
3차원 행렬식
3차 정사각형 행렬의 행렬식은 평행육면체의 부피가 된다.
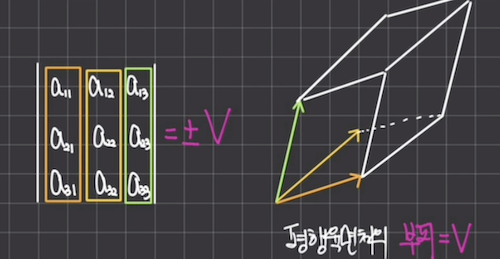
3차원에서는 평행사변형의 넓이에서 평행육면체 부피개념으로 확장된다.
사실 2차원에서 행렬식과 다르지 않다.
다만 행렬식 값이 0이 될경우 3차원이 2차원으로 찌그러지면서 면이되버린다.
Rank
행렬이 가지는 independent 한 column 의 수 혹은 row 의 수
열공간 혹은 행공간 벡터들을 사용해 선형결합하여 만들 수 있는 차원의 수를 뜻한다.
\[A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \end{bmatrix}, B = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix}, C = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix}, D = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]출처: https://www.youtube.com/watch?v=uQhTuRlWMxw&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=7
행렬 $A$ 의 경우 열공간 백터 3개 모두 평행하기에 rank 1 이다.
행공간 백터 2개를 봐도 하나는 영백터이기 때문에 rank 1 이다.
행렬 $B$ 의 경우 3개 벡터 모두 선형 독립이지만 2차원 벡터이다, 3개가 있다 하더라도 만들 수 있는 차원은 2차원이 한계이다.
행공간 백터로 봐도 백터의 개수가 2개뿐임으로 평면으로만 span 할 수 있다.
rank 수, column 수, row 수 에 따라 4가지로 행렬을 명칭한다.
- 행렬 $A$ 의 경우
rank-deficient - 행렬 $B$ 의 경우
full-row-rank - 행렬 $C$ 의 경우
full-columne-rank - 행렬 $D$ 의 경우
full-rank
Rank 에 따른 해의 수
\[A\vec{x} = \vec{v}\]이미 행렬 $A$ 와 선형변환된 백터 $\vec{v}$ 를 알고 있을 때
발생가능한 $\vec{x}$ 의 개수(해의 수) 를 rank 만 알면 알 수 있다.
full-columne-rank
해가 없거나 단하나만 존재
full-row-rank
해가 무한함
full-rank
해가 하나 존재, $\vec{x} = A^{-1}\vec{v}$
rank-deficient
해가 없거나 $\vec{v}$ 가 행공간 혹은 열공간 안에 들어가 있다면 해가 무한함
차원변환
\[\begin{bmatrix} 2\\7 \end{bmatrix} \to L(\vec{v}) \to \begin{bmatrix} 1\\8\\2 \end{bmatrix}\]2차원 백터를 입력으로 3차원 백터로 출력하려면 아래와 같은 비정사각 행렬을 사용해야 한다.
\[L = \begin{bmatrix} 2 & 0 \\ -1 & 1 \\ -2 & 1 \\ \end{bmatrix}\]2차원 기저백터 $i, j$ 가 위의 3차원 기저백터 $i, j$ 로 변한다는 것이 와닿지 않는다.
원점을 지나는 평행한 평면이 존재한다 생각하고
2차원 백터를 3차원으로 확장했다고 억지로 생각하는 것이 최선이다
반대로 3차원 기저백터를 2차원 기저백터로 변경하는 아래 행렬
\[L = \begin{bmatrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ \end{bmatrix}\]3차원 기저백터 $i, j, k$ 가 2차원 기저백터로 변환된다는 뜻이다.
2차원에서 3차원으로 가는것 보다 더 이해가 되지 않지만 아래 내적 개념에서 주로 사용된다.
선형변환에서 내적
2차원 벡터를 예로들면 기하학적으로 내적 = 투영 이라 할 수 있다.
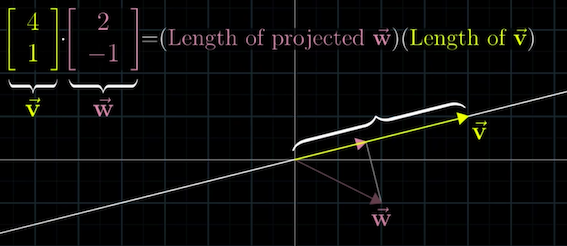
선형변환에서 내적은 일종의 차원변환이라 할 수 있다.
2차원 기저백터에서 1차원(숫자한개) 기저백터로 이동하는 경우
\[\begin{bmatrix} 1 & -2 \end{bmatrix} \to i=[1], j = [-2]\]기저백터가 숫자 하나로 변환된다는 것은 상당히 수상하지만 내적에서 사용하는 개념이 이것이다.
기하학적으로 아래처럼 표현할 수 있다.
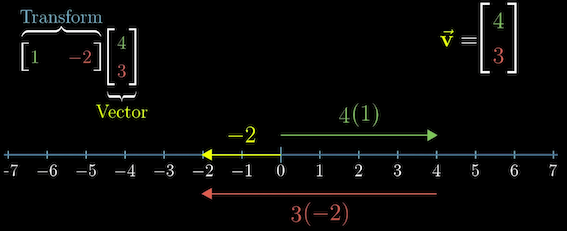
즉 백터의 내적은 아래차원으로의 차원이동이라 할 수 있으며
기하학적으로 내적으로 표현되는 이유는 위 사진으로 설명할 수 있다.
쌍대성(duality)
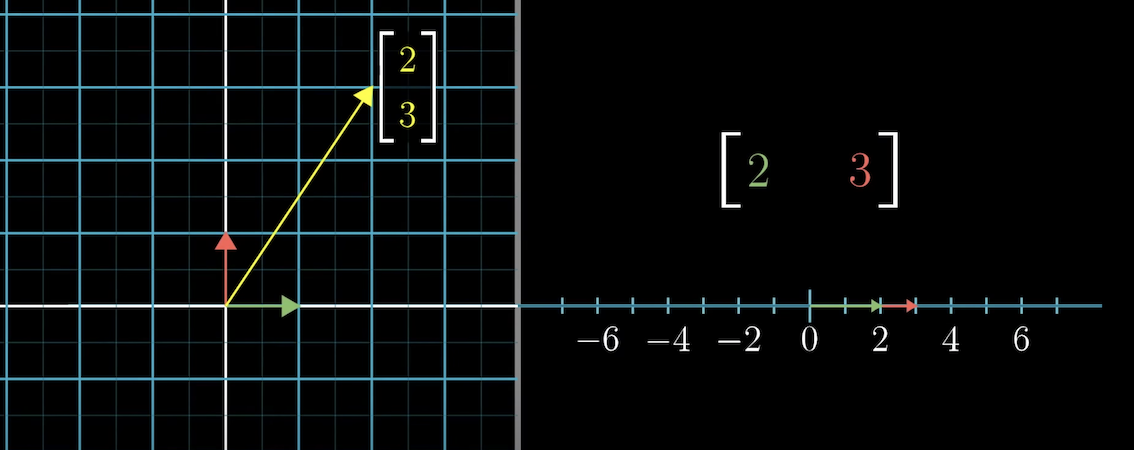
2차원 백터를 1차원으로 변형시키는 행렬곱과, 그냥 2차원 벡터간의 내적은 연산결과가 동일하다.
둘이 어떤 연관이 있는지 기하학적으로 표현해보자.
길이가 1인 단위백터 $\hat{u}$ 임이의 2차원 공간에그리고 쉬운 이해를 돕기 위해 이를 관통하는 1차원 수선을 그리고 단위백터 $i, j$ 을 사용해 관계에 대해 설명해보겠다.
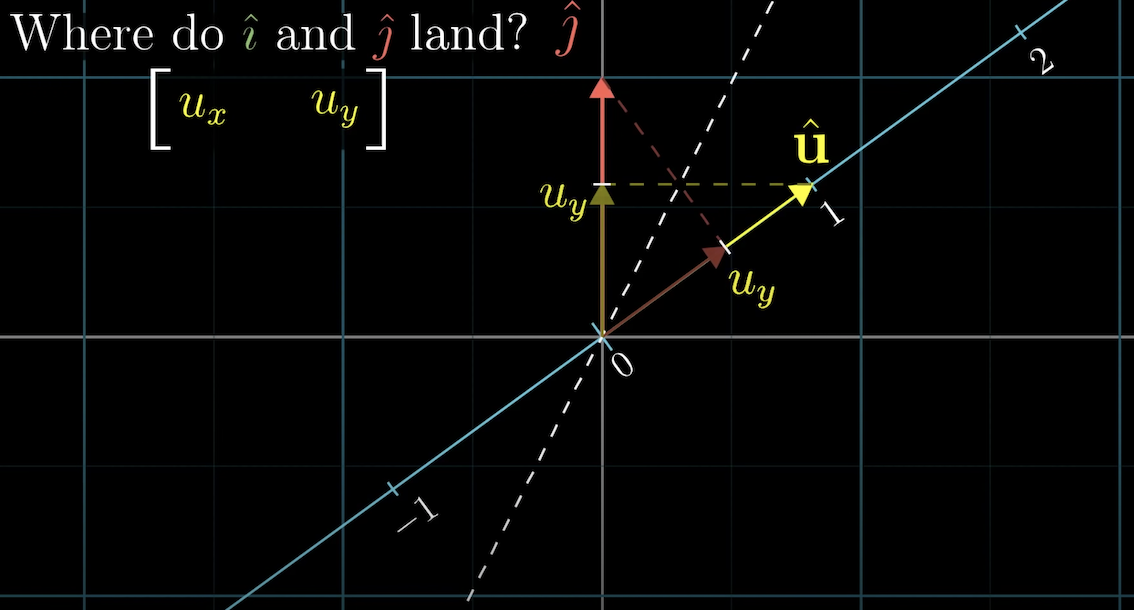
$\vec{u}$ 의 투영된 값을 사용해 1차원 행렬 $\begin{bmatrix}u_x & u_y\end{bmatrix}$ 를 만들었는데
이 값이 곧 단위백터 $\hat{i}$ 혹은 $\hat{j}$ 를 1차원 단위백터 $\hat{u}$ 로 변환하는 행렬이다.
또한 이를 전치하면 $\hat{u}$ 의 2차원 공간에서의 백터 $\begin{bmatrix}u_x \ u_y\end{bmatrix}$ 이기도 하다.
이것이 1차원 행렬과 2차원 백터간의 관계이다.
임이의 2차원 백터 $\begin{bmatrix}x & y\end{bmatrix}$ 와 $\hat{u}$ 과의 행렬곱과 내적은 아래와 같은 수식으로 표현가능하다.
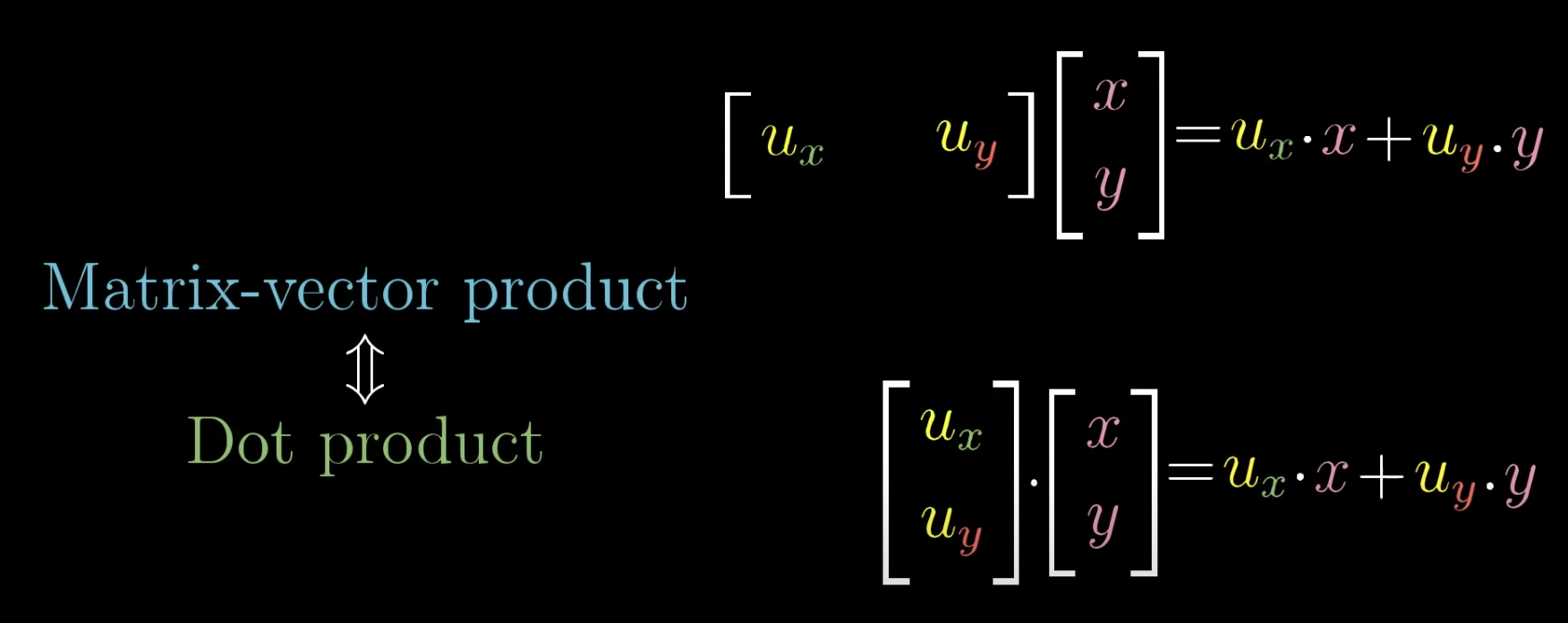
$\hat{u}$ 의 길이가 꼭 1이 아닌 $n$ 이더라도 위에서 $n$ 만큼 배수해주면 되며 내적공식 평행 투영 길이 x 백터 길이 이 나온 이유이기도 하다.
다시 위에서 사진을 보면서 백터와 1차원 변환 행렬간의 관계가 어떤 연관관계인지
행렬곱과 내적이 같은 결과를 축력하는지 생각해보자.
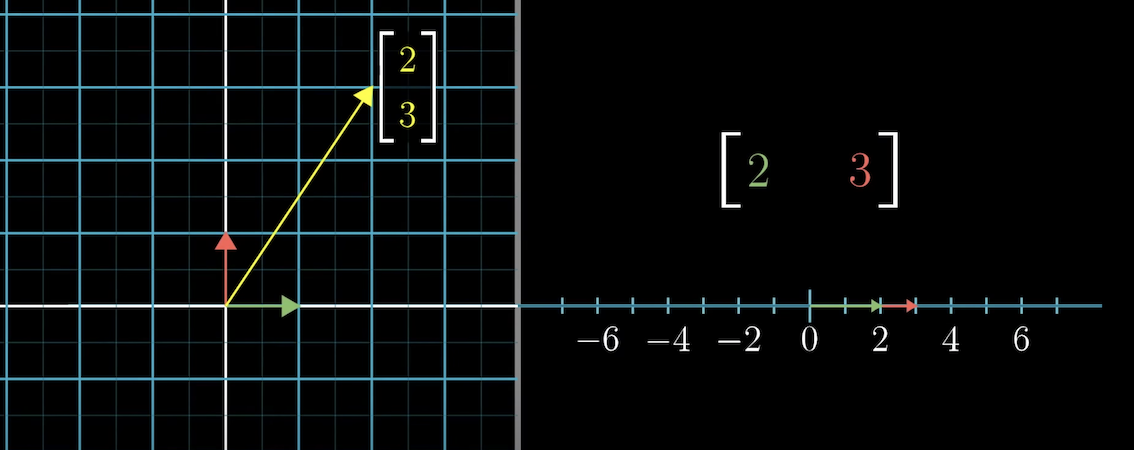
이중(dual) 이란 백터가 가진 선형변환 성질을 뜻하며 아래 2가지 특징으로 설명할 수 있다.
2차원 백터를 1차원으로 선형변환시켜버리는 성질,
2차원 백터공간에서 내적을 위한 2차원 백터의 역할이다.
2차원 백터가 단순히 2차원 공간상의 화살표가 아닌 1차원 공간으로의 변환(투영) 으로 보이는 내적연산으로 생각할 수 있도록 연습하자.
선형변환에서 외적
$\vec{v} \times \vec{w}$ 는 그림과 같이 평행사변형의 넓이를 나타내며
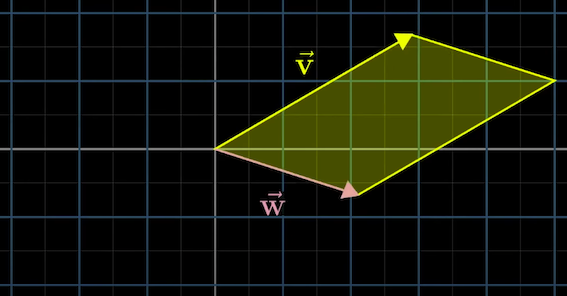
외적이라는 단어를 사용하지만 사실
결과값은 $\hat{i}, \hat{j}$ 단위백터가 해당 $\vec{v}, \vec{w}$ 백터들로 선형변환 되는 행렬의 행렬식이다.
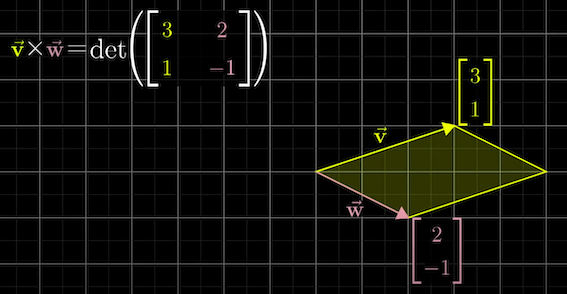
하지만 본질은 단순 2차원 백터에서 평행사변형의 크기를 구하는 것이 아닌 3차원에서 두 백터에 직각에 해당하는 새로운 백터를 구하는 것이다. (길이는 두 백터가 이루는 평행사변형의 크기)
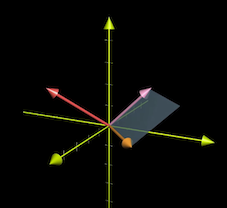
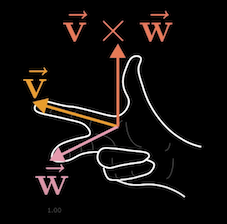
방향은 오른손법칙을 따르며 $\vec{v}$ 와 $\vec{w}$ 에 의해 결정된다.
기하학적인 설명은 여기까지고 실제 출력된 백터는 아래와 같다.
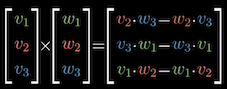
위의 외적을 구하는 이상한 연산에 $i, j$, $\hat{k}$ 을 사용하면
\[\begin{aligned} \vec{a} \times \vec{b} &= \det( \begin{bmatrix} \hat{i} & a_1 & b_1 \\ \hat{j} & a_2 & b_2 \\ \hat{k} & a_3 & b_3 \\ \end{bmatrix}) \\\\ &= \hat{i}(a_2b_3 - a_3b_2) + \hat{j}(a_3b_1 - a_1b_3) + \hat{k}(a_1b_2 - a_2b_1) \\\\ &= \begin{bmatrix} (a_2b_3 - a_3b_2) \\ (a_3b_1 - a_1b_3) \\ (a_1b_2 - a_2b_1) \end{bmatrix} \end{aligned}\]외적에 해당하는 기저벡터의 조합을 얻게된다.
행렬요소값으로 숫자가 아닌 벡터를 넣는데 이를 표기적 트릭 이라한다.
duality with deteminate
위에서 2차원 백터와 1차원 변환 행렬의 duality 성질을 알아보았는데
이번엔 3차원 백터와 1차원 변환 행렬, 그리고 같은 1차원 값을 내보내는 행렬식의 duality 설질에 대해 알아보자.
이를 이해하기 위해 먼저 아래 식을 알아야 한다.
\(f(\begin{bmatrix} x \\ y \\ z \end{bmatrix}) = \det(\begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \\ \end{bmatrix})\) 다음과 같이 임의의 백터와 $\vec{v}$, $\vec{w}$ 의 행렬식을 구하는 행렬 $f$ 가 있다면
백터의 duality 성질을 이용해 외적값과 외적값으로 변환되는 1차원 변환 행렬 $\begin{bmatrix}?&?&?\end{bmatrix}$ 을 매칭, duality 성질을 사용해 내적하는 값으로 표현 할 수 있다.
1차원 변환행렬(내적) 그리고 행렬식이 서로 연관된 duality 성질을 사용했다.
이 임의의 백터를 $\vec{v}$, $\vec{w}$ 의 외적을 통해 구한 수직된 백터 $\vec{p}$ 로 생각하고 $\vec{p}$와 특정 백터 의 내적과 행렬식의 관계를 아래처럼 표현 가능하다.
\[\begin{aligned} \begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} &= \det(\begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \\ \end{bmatrix}) \\\\ p_1x + p_2y + p_3z &= x(v_2w_3 - v_3w_2) + y(v_3w_1 - v_1w_3) + z(v_1w_2 - v_2w_1) \\\\ p_1 &= v_2w_3 - v_3w_2 \\ p_2 &= v_3w_1 - v_1w_3 \\ p_3 &= v_1w_2 - v_2w_1 \end{aligned}\]위 수식이 도출되는지 이해는 되지만 기하학적으로 생각하지 힘들다.
이는 내적, 외적, 행렬식 3개가 같이 사용되어 그런데 아래에서 좀더 기하학적으로 설명해보겠다.
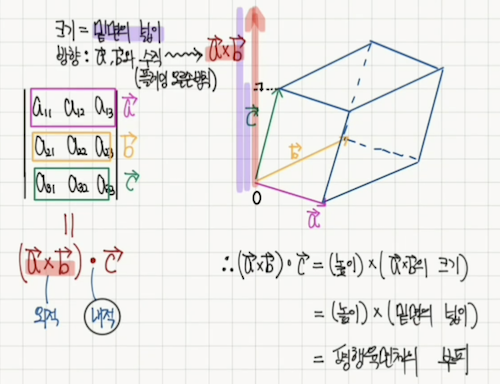
\[\begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \det(\begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \\ \end{bmatrix})\]앞으로 소개할 내용은 평행육면제의 부피를 구하는 공식과 연관이 있는데
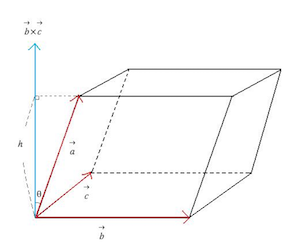
위 그림을 기억해두자
임의의 백터와 내적한 값이 $\vec{v}$, $\vec{w}$ 와 임의의 백터를 사용한 행렬식(평행육면체 부피) 값과 같은 값을 가지게 되는 $\vec{p}$ 는?
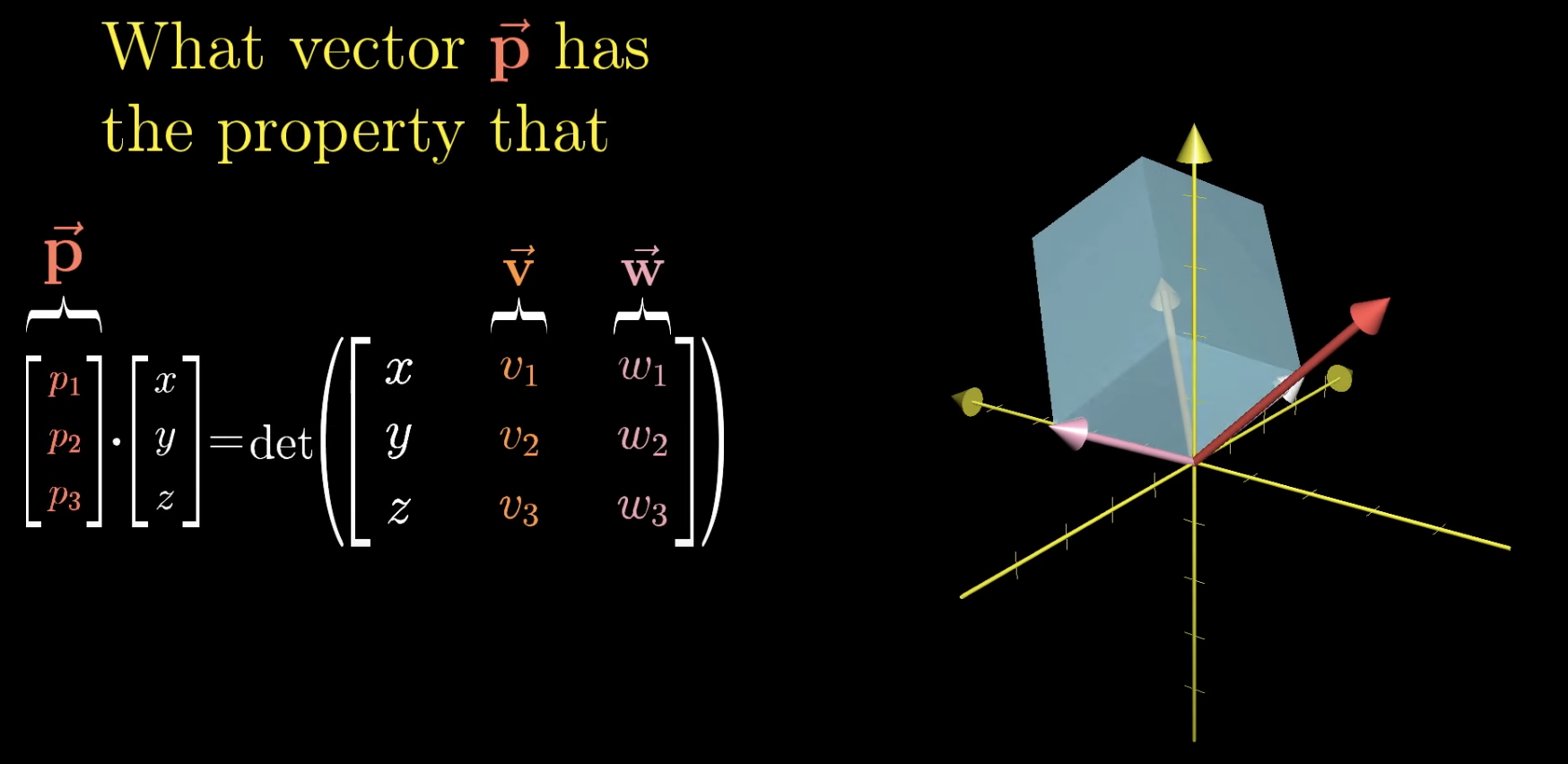
내적이란 $\vec{p}$ 에 투영된 임의의 백터의 길이와 $\vec{p}$ 의 길이를 곱한 값 이다.
그리고 이 투영된 길이는 평행육면체의 높이에 해당한다.
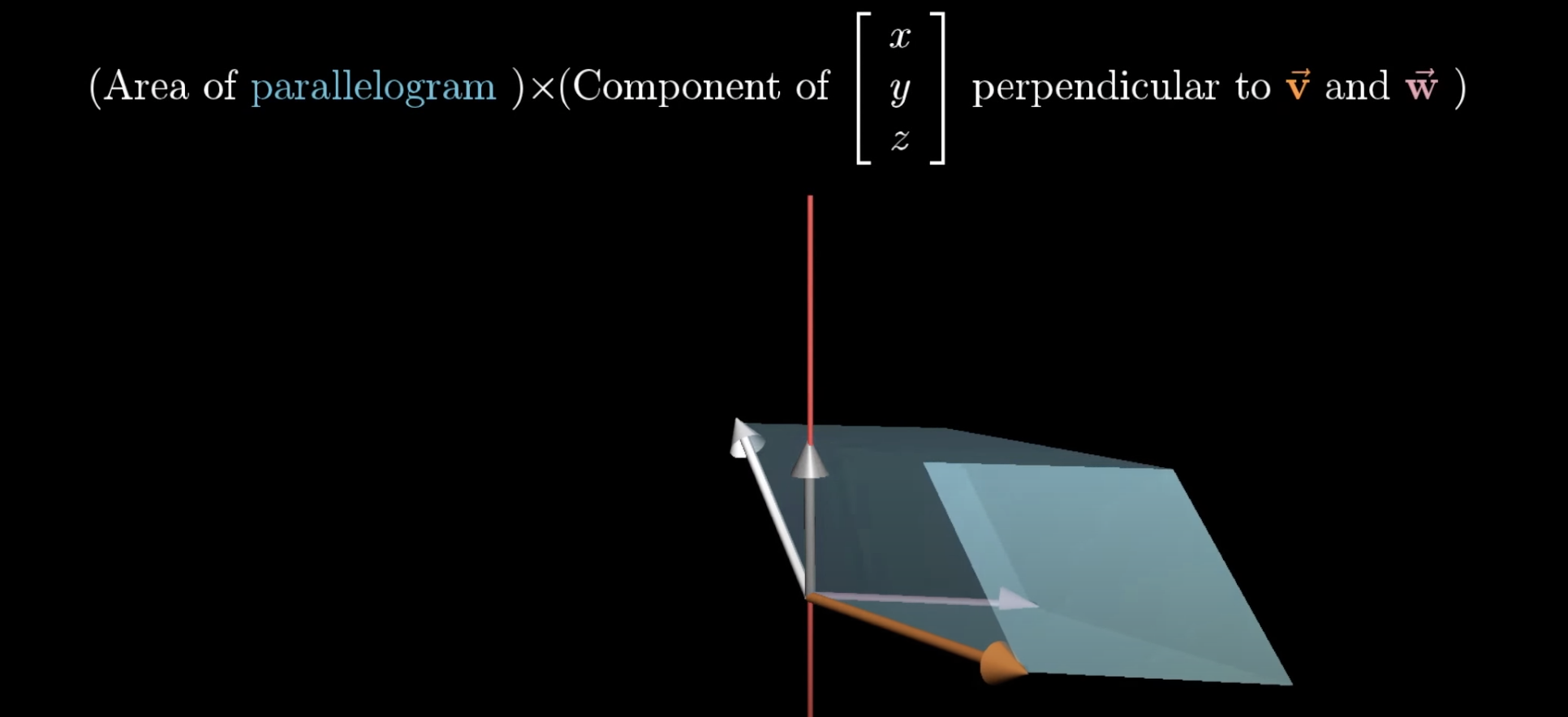
그렇다면 평행육면체 높이 와 $\vec{p}$ 의 길이를 서로 곱한값이 되는데
$\vec{p}$ 의 길이는 곧 $\vec{v}$, $\vec{w}$ 의 외적으로 구한, 평행사변형의 넓이이다.
선형변환에서 역행렬
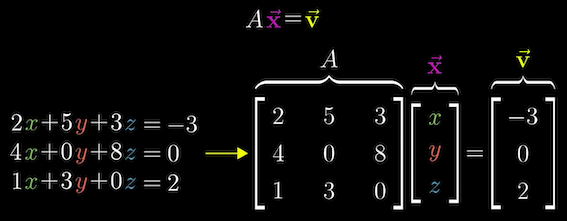
위에서 본 행렬에 백터를 집어넣어 새로운 백터를 출력하는 공식을 사용하면 위와같이 선형방적식을 통해
복잡한 방정식의 해를 행렬을 통해 쉽게 구해낼 수 있다.
$A$ 행렬의 역행렬 $A^{-1}$ 를 구하면 쉽게 $x, y, z$ 를 구할 수 있다.
\[\begin{aligned} A \cdot A^{-1} \cdot \vec{x} &= A^{-1} \cdot \vec{v} \\ \vec{x} &= A^{-1} \cdot \vec{v} \end{aligned}\]행렬식이 0 이 아니라면 백터를 원복하는 역행렬은 항상 존재함으로
행렬이란 $i, j$ 단위백터([0,1] [1,0])를 특정값으로 변화시키는 선형변환 함수이다.
2차원 행렬에서 두 단위백터가 서로 일자가 되는 상황(행렬식=0)이 된다 생각해보면
왜 찌그러지는지 쉽게 연상할 수 있다.
역행렬의 기하학적 의미를 이해하기위해 먼저 좌표계의 선형변환을 다시 떠올려야 한다.
우리가 흔히아는 단위백터의 길이가 1 로 표현되는 $i, j$ 로 표현되는 좌표계와
아래 그림처럼 $\vec{b_1}=\begin{bmatrix} 0 \ 1 \end{bmatrix}_i$, $\vec{b_2}=\begin{bmatrix} 1 \ 0 \end{bmatrix}_j$ 를 단위백터로 사용하는 제니퍼 좌표계가 있을때
기존 좌표계에선 $\vec{b_1}$ 은 $\begin{bmatrix} 2 \ 1 \end{bmatrix},$ $\vec{b_2}$ 는 $\begin{bmatrix} -1 \ 1 \end{bmatrix}$ 이다
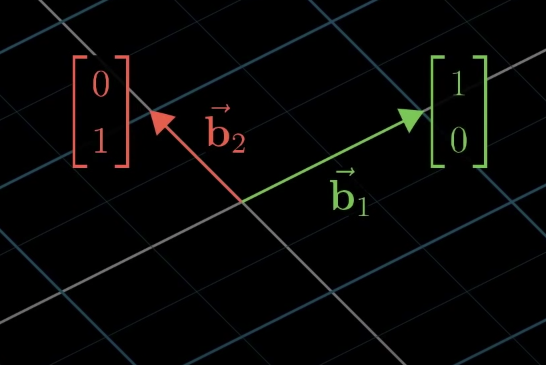
제니퍼 좌표계 -> 기존 좌표계 표현, 어떻게 계산해야 할까?
기존에 학습했던 행렬을 이용한 선형변환을 사용해
$\begin{bmatrix} -1 \ 2 \end{bmatrix}_j$ 제니퍼 좌표를 아래와 같이 표현 가능하다.
지금까지 벡터와 선형변환 결과값, 모두 기존좌표계로만 표기하는 것에 매몰되어 있었다.
기존 좌표계의 벡터를 선형변환 후 다시 기존 좌표계의 벡터 표현했디 생각할 수 있지만
사실은 제니퍼 좌표계의 백터를 기존 좌표계의 백터로 수치학적으로 표현하기 위해 행렬을 사용하였던 것이다.
위 기존 좌표계의 백터를 제니퍼 좌표로 변환하는 방법은 행렬의 선형변환이 아닌 역행렬의 선형변환이다.
(우리의 좌표계를 제니퍼 좌표계로 변환하는 것이다)
이것이 기존 좌표계의 벡터가 제니퍼 좌표계에서 취급되는 숫자이다.
간단히 수식으로 설명하면 아래와 같다.
\(A\begin{bmatrix}x_j \\ y_j\end{bmatrix} = \begin{bmatrix}x_o \\ y_o\end{bmatrix} \\\) \(\begin{bmatrix}x_o \\ y_o\end{bmatrix} = A^{-1}\begin{bmatrix}x_j \\ y_j\end{bmatrix}\)
행렬을 통한 선형변환 = 제니퍼 좌표계 > 기존 좌표계로 표현하기 위한것
역행렬을 통한 선형변환 = 기존 좌표계 > 제니퍼 좌표계로 표현하기 위한것
역행렬의 선형변환
제니퍼 좌표계에서 90° 회전의 경우를 생각해보자.
기존좌표계 에서는 $\begin{bmatrix}0&-1\1&0\end{bmatrix}$ 행렬을 사용해 선형변환을 해왔는데
해당 행렬은 기존 좌표계의 단위백터 $i, j$ 이 변환하는 행렬이기 때문에 우리는 제니퍼 단위백터가 90° 회전하는 행렬을 구해야 한다.
해당 행렬을 제니퍼 좌표계 $\begin{bmatrix}2 & -1 \ 1 & 1\end{bmatrix}$ 행렬과 연계하여 변환하면 되지 않을까란 생각을 해보지만
그냥 90° 회전후에 제니퍼 좌표로 선형변환 한 것일뿐 제니퍼좌표계의 백터를 90° 회전하는 행렬은 아니다.
제니퍼 좌표를 90° 회전하려면 아래와 같이 기존좌표게변경 -> 선형변환 -> 제니퍼좌표계 변경 하는 행렬의 연계를 해야한다.

제니퍼 백터 $\vec{v}$ 를 기존 좌표계로 변환후 90°회전, 역행렬을 통해 기존좌표계에서 제니퍼 좌표계로 변환하면
제니퍼 좌표계에서 90° 회전시키는 선형변환 행렬이 생성된다.
정확이 90° 회전된 제니퍼 백터 $\begin{bmatrix} -1 \ 1\end{bmatrix}_j$ 이 출력된다.
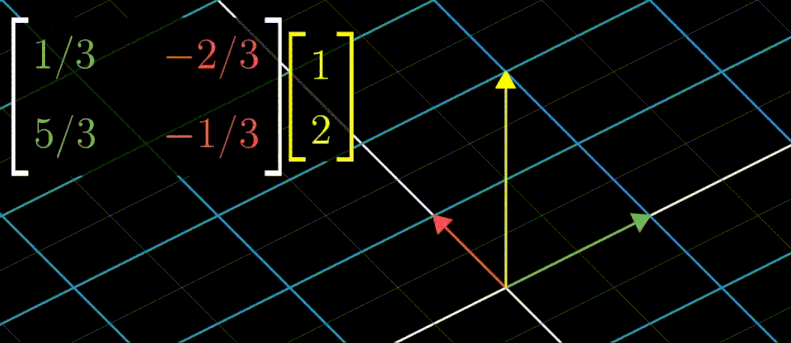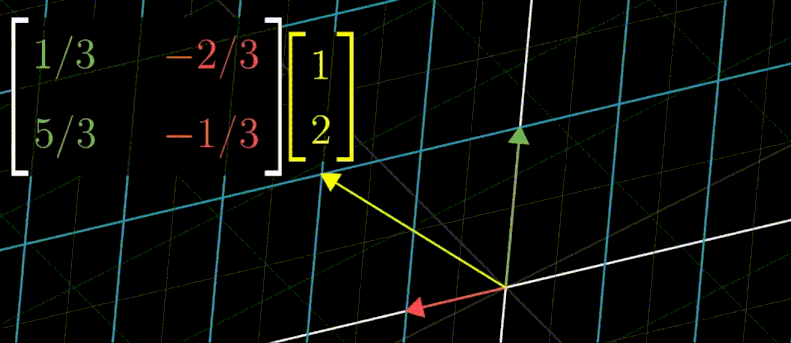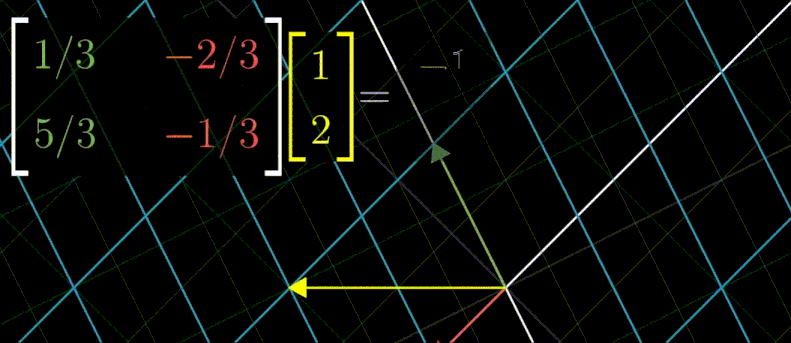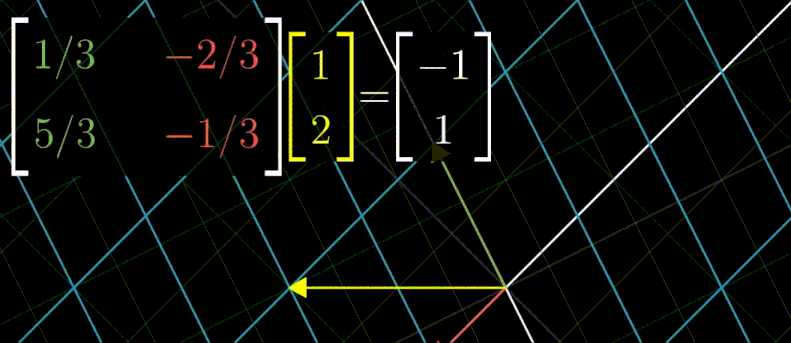
대각행렬은 아래 그림처럼 100번을 곱해도
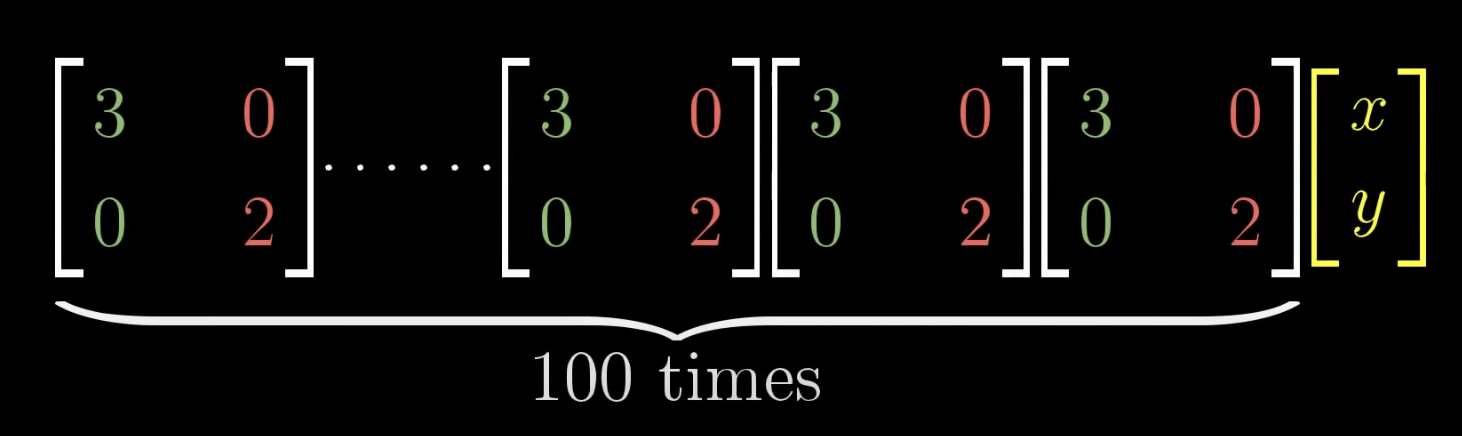
단순한 수식으로 표현할 수 있다.
만약 대각행렬이 아닌 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 같은 행렬을 100번 곱하여 백터를 선형변환 하고 싶다면 엄청난 수의 연산과정을 거쳐야 할 것이다.
이 경우 기저를 변경하여 일반행렬을 대각행렬로 변경할 수 있는데 대각화라 하며 고유백터를 사용한다.
$\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 의 고유백터 $\begin{bmatrix}1 \ 0\end{bmatrix}, \begin{bmatrix}-1 \ 1\end{bmatrix}$ 를 사용해서
고유백터가 기저백터가 되도록 좌표계를 변경한다.
좌표계를 변경한다는 것은 양옆으로 행렬과 그에 해당하는 역행렬을 곱합으로써 이루어진다.
위의 제니퍼 좌표계 변환법을 생각해보자.
위의 연산은 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 의 기저백터로 좌표계를 변환후 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}$ 선형변환을 한것이기에
변환된 좌표계 입장에서 x 축 y 축 기반으로 늘어날 뿐이다.
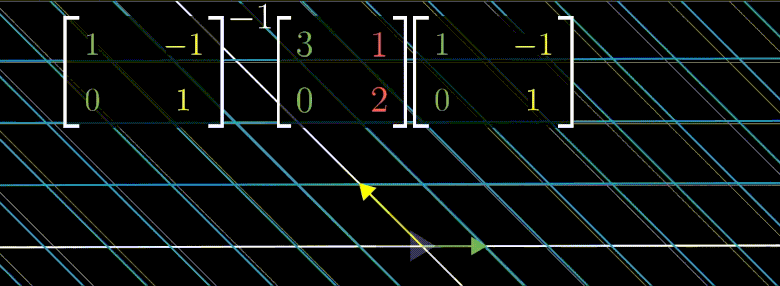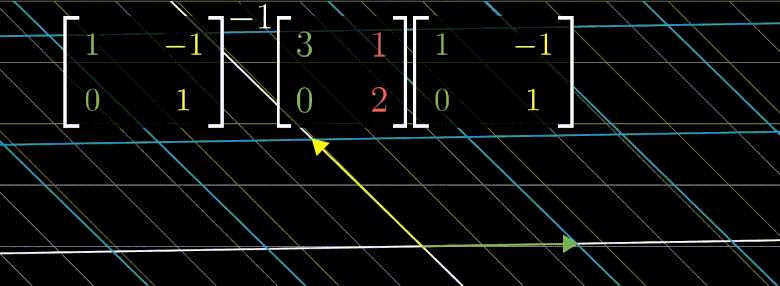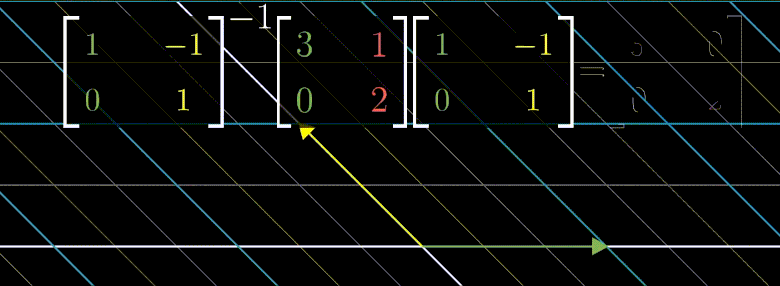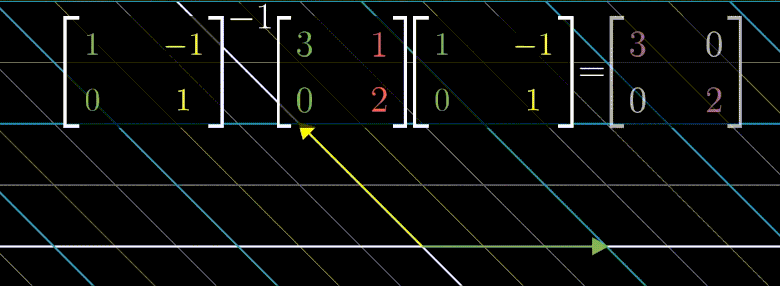
만약 $\begin{bmatrix} 3 & 1 \ 0 & 2 \end{bmatrix}^{100}$ 한 결과를 알고싶다면 고유기저로 변경 후 계산하고 다시 원래 좌표계로 변환하는 것이 더 효율적이다.