행렬의 크기
행렬을 일종의 숫자 하나(스칼라) 로 변경하는 여러가지 방법에 대해 설명한다.
Norm (Euclideam Norm)
행렬에서의 Norm은 수학적 크기를 뜻한다.
행렬에서의 Norm은 아래와 같이 표현
A행령의 크기가 $n \times m$ 일 때
모든 원소의 제곱을 더한하고 루트를 취한값이다.
기호 e는 Euclideam 의 약자이며
Euclideam Norm L2 Norm 이라고도 한다.
P Norm
2제곱이 아닌 p제곱후 p제곱근을 취한값
\[\|A\|_p = \sqrt[p]{\sum_{i=1}^n\sum_{i=j}^m a_{i,j}^p}\]p=1 - 절대값의 합
p=2 - Euclideam Norm L2 Norm
p=무한대 - 요소중 가장 큰값에 가까워진다.
열합 Norm, 행합 Norm
\[A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\]위와같은 행렬 A 가 있을때 Norm에선 행렬의 행 또는 열을 가지고 값을 표현할 수 있는 수식이 있다.
\[\|A\|_1 = \max_{1\le j \le n}\sum_{i=1}^n|a_{i,j}|\] \[a=a_{11} + a_{21} + a_{31} \\ b=a_{12} + a_{22} + a_{32} \\ c=a_{13} + a_{23} + a_{33} \\\]$a,b,c$ 중 가장 큰 값을 열합Norm의 값으로 표기한다.
행합Norm의 식은 아래처럼 표기
\[\|A\|_\infty = \max_{1\le i \le n}\sum_{i=1}^n|a_{i,j}|\] \[a=a_{11} + a_{12} + a_{13} \\ b=a_{21} + a_{22} + a_{23} \\ c=a_{31} + a_{32} + a_{33} \\\]$a,b,c$ 중 가장 큰 값을 행합Norm의 값으로 표기한다.
대각합(trace)
대각합(trace) 정사각해열에서만 가능하며 행렬의 대각성분들을 모두 더한값이다.
\[tr(A) = \sum^n_{i=1} a_{ii}\]대각합 성분
\[tr(A+B) = tr(A) + tr(B) \\ tr(CA) = C tr(A) \\ tr(A^T) = tr(A) \\ tr(AB) = tr(BA) \\ tr(ABCD) = tr(BCDA) = tr(CDAB) = tr(DABC) \\\]마지막항은 cyclic property 라 하는데 행렬의 곱셉 순서를 cycle 형식으로 변경할 수 있다.
최소자승법(Least Square Method, 최소제곱법)
그림처럼 행렬 $A$ 의 열공간 $C(A)$, 그리고 열공간을 벗어나는 백터 $b$ 가 있을 때
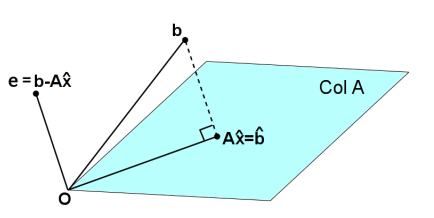
$C(A)$ 안에서 표현할 수 있는 백터 $Ax$ 중
백터 $b$ 와 가장 거리가 짧은 백터를 $A\hat{x}$ 라 할 때 $A\hat{x}$ 을 구하는 방법이 최소자승법(Least Square Method) 이다.
$\hat{x}$ 을 알아야 하지만 관측값(measurement)이 노이즈가 발생해서 위 그림처럼 $b$ 로 나왔을 때 최소자승법을 사용해 다시 $\hat{x}$ 를 구할 수 있다.
$b$ 와 $A\hat{x}$ 간격을 표현하는 백터는 $e = b-A\hat{x}$ 로 쓰 수 있고
이 백터 $e$ 의 길이(L2Norm) 이 가장 짧아지는 $\hat{x}$ 를 구하면 된다.
백터 $e$ 와 $A\hat{x}$ 은 수직하기 때문에 내적이 0 임으로 아래와 같은 방정식 정의 가능
\[(b - A\hat{x}) \cdot A\hat{x} = 0 \\ (b - A\hat{x})^T A\hat{x} = 0 \\ (b^T - (A\hat{x})^T) A\hat{x} = 0 \\ (b^T A - \hat{x}^T A^T A) \hat{x} = 0 \\\]$\hat{x}$ 이 영백터가 되면 의미가 없음으로
\[b^T A - \hat{x}^T A^T A = 0 \\ \hat{x}^T A^T A = b^T A \\ \hat{x}^T = b^T A (A^T A)^{-1} \\ \hat{x} = (A^T A)^{-1} A^T b \\\]$A^TA$ 는 정사각행렬이 됨으로 역행렬 표현에 문제가 없다.
그림의 벡터 $b$ 의 정사영(projection) 된 벡터는 $A\hat{x}$ 임으로
\[A\hat{x} = A(A^T A)^{-1} A^T b\]이런 특징때문에 $A(A^T A)^{-1} A^T$ 를 투영행렬(projection matrix) $P_A$ 이라 한다.