행렬식(determinant)
출처: https://www.youtube.com/watch?v=fuVMiyahzH4
행렬의 스칼라값을 만드는 함수
역행렬의 존재여부를 판단하는 함수
행렬식은 정사각행렬에서만 정의된다.
\[A=\begin{bmatrix} a&b \\ c&d \end{bmatrix}\]2차 정사각형 행렬의 행렬식은 팽형사변형의 넓이가 된다.
아래과 같은 기호로 사용
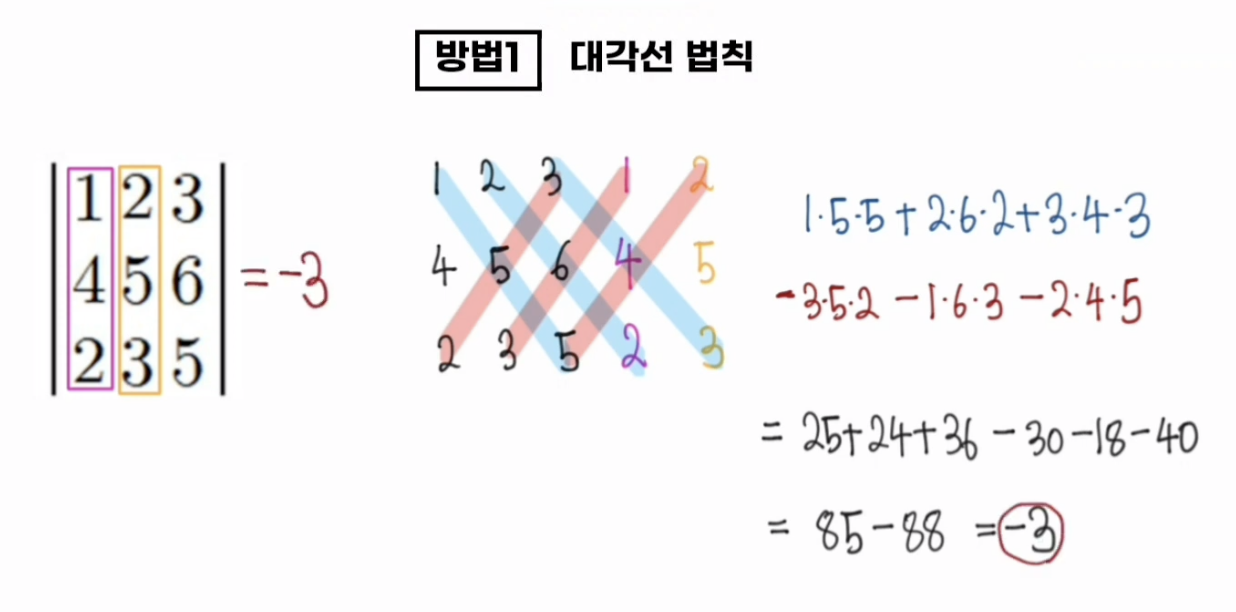
행렬식 계산 - 대각선 법칙
3차행렬 까지는 대각선 법칙을 사용해서 구할 수 있다.
행렬식 계산 - 여인수 전개(cofactor expansion)
4차 이상 행렬부터는 여인수 전개(cofactor expansion) 를 통해서 행렬식을 구한다.
cofactor: 보조인자
라플라스 전개(laplace expansion)라고도 함
n x n 행렬이 있을때 제외할 행 혹을 열을 하나 정하고
0 ~ n 까지의 열 혹은 행을 제외하여 n개의 새로운 부분행렬을 만든 후 전개하여 구한다.
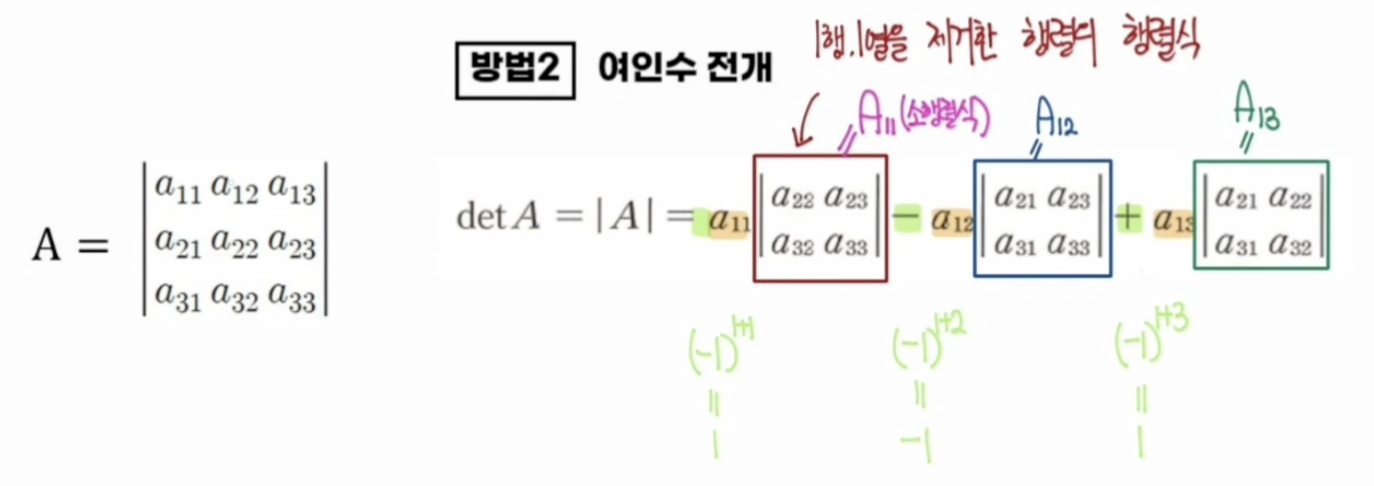
위 그림에선 1행1열, 1행2열, 1행3열을 제외한 각각의 행렬을 구해 계산하였지만
반대로 열을 고정하여 2열1행, 2열2행, 2열3행 을 제외한 각각의 행렬을 구해 행렬식을 계산해도 같은값이 나온다.
제외되어 나온 행렬의 행렬식을 소행렬식(minor determinant) 이라 하며 $M_{ij}$ 기호로 표기한다
i행 j열이 제외된 부분행렬의 행렬식
소행렬식 앞의 +, - 부호는 -1 에 행과 열을 더한 값을 지수에 적용
(부호 + 소행렬식) 까지가 여인수(cofactor) 이라 하며 아래 식으로 표기
따라서 행렬 $A$ 의 행렬식을 아래처럼 표현할 수 있다.
\[\det(A) = a_{11} C_{11} + a_{12} C_{12} + a_{13} C_{13}\]공식은 아래와 같다, 행 혹은 열을 기준으로 $i$ 나 $j$ 를 증가시키면 된다.
\[\det(A) = \sum (-1)^{i+j} a_{ij} C_{ij}\]여인수 전개는 0이 많이 포함된 행이나 열을 사용해 행렬식을 구하면 편하다.
행렬식과 기본행 연산
행렬식과 기본행 연산의 관계를 알아보자.
행간 교환, 곱하기 에 의해 행렬식이 어떻게 변하는지에 대해 알아보자.
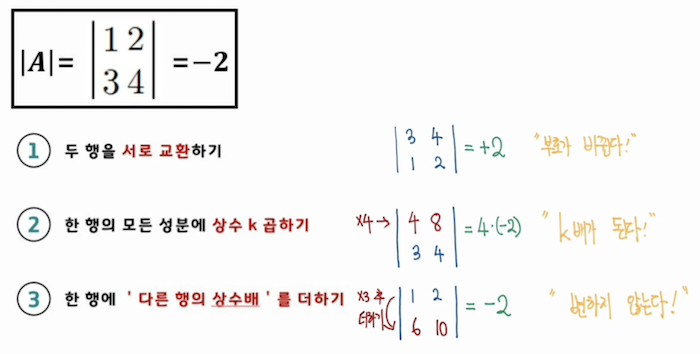
다음에 나올 가우스 소거법을 위해 3 규칙이 매우 중요하다.
2법칙의 왜 두 행을 교환하면 부호가 반대되는가?
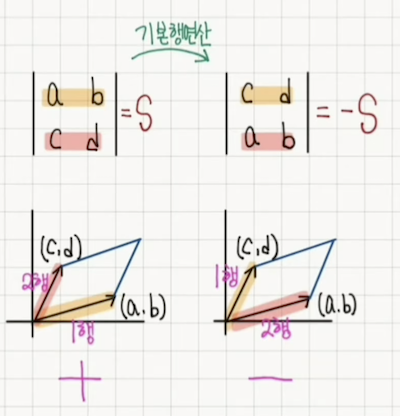
기하학적으로 보면 1행의 각도가 2행의 각도보다 크다면 - 반대라면 + 이다.
행 사다리꼴
행 사다리꼴(row echelon form matrix)
- 각 행의 0을 제외한 첫번째 요소는 무조건 1이어야 한다(선두성분이라함)
- 0으로만 이루어진 행이 있을경우 가장 밑에 있어야 한다.
- 선두성분은 아래백터의 순서보다 항상 먼저있어야 한다.
기약행 사다리꼴
기약 행 사다리꼴(reduced row echelon form matrix)
행 사다리꼴에 아래 조건이 추가된다.
- 열로 보았을때 1이 있다면 나머지 열의 요소는 모두 0 이어야 한다.
역행렬(inverse matrix)
행렬 A 의 역수 역행렬 $A^{-1}$
역행렬의 의미는 $ A \cdot A^{-1} = I$
$\det(A)=0$ 경우 역행렬은 존재하지 않고(not invertible) sigular matrix 라 하고
$\det(A)\ne0$ 경우 역행렬을 존재하고(invertible) nonsigular matrix 라 한다.
행렬식으로부터 이라는 뜻은 역행렬이 있는지 없는지를 판별하기 때문에
determinant라는 이름을 사용한다.
가우스 소거법으로 역행렬 구하기
2 x 2 행렬식에서 아래와 같이 정의가 되어 있다.
\[A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, A^{-1}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\]임시로 A 의 역행렬을 $a,b,c,d$ 를 사용해 표기
행렬간 곱셈의 결과가 단위행렬임으로 다음 식이 도출됨
\(1 \times a + 2 \times c = 1 \\
1 \times b + 2 \times d = 0 \\
3 \times a + 4 \times c = 0 \\
3 \times b + 4 \times d = 1\)
위 4개 식을 사용해 $a,b,c,d$ 를 구하면 역행렬을 정의할 수 있다.
좀더 쉽게 역행렬을 계산하기 위한 방법으로
행렬를 사용해서 연립일차 방정식의 해를 구할 수 있는데
행렬의 여러 값을 소거해가면서 기약행사다리꼴로 만들어
연립방정식의 해를 구하기 위한 방법을 가우스 소거법이라 한다.
단위행렬이 기약행사다리꼴임으로 단위행렬을 만들면 된다.
확장행렬을 사용해 모든 열에 1이 하나면 존재하도록 소거해나간다.
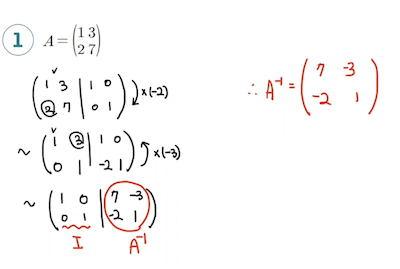

가우스 소거법으로 기약 행 사다리꼴이 구해지지 않는경우 역행렬이 존재하지 않는다.
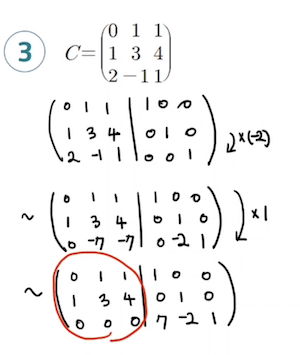
마지막의 경우 역행렬이 존재하지 않는다.
행렬식으로 역행렬 구하기
위에서 여인수행렬로 행렬식을 구할 때
$A$ 행렬에서 i행 j열이 제외된 소행렬의 행렬식 $A_{ij}$ 그리고 해당 소행렬의 행렬식을 기반으로 행렬식을 구했었다.
여인수들로 구성된 행렬로 수반행렬(adjoint matrix) 라 부르며 약자로 $adj$ 를 사용한다.
\[A_{adj} = \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} ^ T = \begin{bmatrix} C_{11} & C_{21} & C_{31} \\ C_{12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \end{bmatrix}\]여인수행렬이라고도 한다.
전치까지 취해주어야 수반행렬이라 한다.
행렬 $A$ 와 수반행렬 $A_{adj}$ 를 서로 곱하면
대각성분은 행렬식이 되고 그외값은 0이 된다.
\[A \cdot A_{adj} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \cdot \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix}^T = \begin{bmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{bmatrix}^T \\ \ \\ A \cdot A_{adj} = |A| \cdot I\]0이 되는 이유 https://www.youtube.com/watch?v=sWqhINQWSI4 전치를 취한 이유
그렇다면 위 식의 양변에 $|A|$ 를 나누면 우변이 단위행렬이니
아래처럼 역행렬을 정의할 수 있다.
유사 역행렬(pseudo inverse)
\[A^T(AA^T)^{-1}\]행렬 A 의 right-pseudo inverse
$A^{-1}$ 은 아니지만 동일한 역할은 하는 행렬이다.
행렬식, 역행렬 특징
대각행렬, 삼각행렬(triangular matrix) 는 대각성분의 곱이다.
다음 조건일 때 역행렬은 존재(invertible)하고 행렬 $A$ 는 nonsigular matrix 이다.
반대로 $\det(A) = 0$ 일 때 A 는
rank-deficient
행렬식, 역행렬 속성
\[(AB)^{-1} = B^{-1}A^{-1} \\ CC^{-1} = C^{-1}C = I \\ (A^{-1})^{-1} = A \\ (KA)^{-1} = \frac{1}{K} A^{-1} \\ (A^T)^{-1} = (A^{-1})^T \\ \det(A^{-1}) = \frac{1}{\det(A)} \\ \det(A^T) = \det(A) \\ \det(AB) = \det(A) \times \det(B) \\ \det(cA) = c^n \det(A)\]대칭행렬의 역행렬
\[A = A^T\]위 대칭행렬 공식으로부터 아래 유도 가능
\[AA^{-1} = I \\ (AA^{-1})^T = I^T = I \\ (A^{-1})^TA^T = I \\ (A^{-1})^TA = I \\ (A^{-1})^T = A^{-1} \\\]역행렬과 역행렬의 전치가 동일하다.