행렬(Matrix)
행렬: 수나 문자를 직사각형으로 나열한것
2행 3열을 가진 행렬
\[\begin{pmatrix} 1 & 3 & 4 \\ -1 & 0 & 5 \end{pmatrix}\]인덱스로 표현은 아래와 같이 한다.
\[\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix}\]전치행렬(Transposed Matrix)
$A$의 전치행렬 $A^T$
\[A = \begin{pmatrix} 1 & 3 & 4 \\ -1 & 0 & 5 \end{pmatrix}\] \[A^T = \begin{pmatrix} 1 & -1 \\ 3 & 0 \\ 4 & 5 \end{pmatrix}\]전치행렬 속성
\[\begin{aligned} & (A^T)^T = A \\ & (A+B)^T = A^T + B^T \\ & (AB)^T = B^TA^T \\ & det(A^T) = det(A) \\ & (A^T)^{-1} = (A^{-1})^T \to A^{-T \\} \end{aligned}\]대칭행렬(Symmetric matrix)
\[A^T = A \\ a_{ij} = a_{ji}\]위 조건을 만족하는 행렬
\[A = \begin{pmatrix} 1 & 3 \\ 3 & a \end{pmatrix} A^T = \begin{pmatrix} 1 & 3 \\ 3 & a \end{pmatrix}\] \[A = \begin{pmatrix} 1 & 3 & 7 \\ 3 & 0 & -1 \\ 7 & -1 & 1 \end{pmatrix} A^T = \begin{pmatrix} 1 & 3 & 7 \\ 3 & 0 & -1 \\ 7 & -1 & 1 \end{pmatrix}\]대각으로 대칭되는 것. 그렇기에 정사각형 형식의 행렬이다.
대각행렬(diagonal matrix)
대각성분 외의 모든 성분이 0 인 행렬, 기호는 D 를 사용
\[D= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix}\]단위행렬(unit matrix, identity matrix)
대각성분이 1이고 그외는 모두 0인 행렬, 행렬에서 숫자 1과 같은 역할, 기호로 I 를 사용
\[I = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]행렬 $A$가 있을때 영행렬과 더하거나 단위행렬과 곱하면 그대로이다.
\[A \cdot I = A\]대각행렬과 단위행렬은 정사각행렬.
정규직교행렬(Orthonormal Matrix)
선형대수학에서 정규직교행렬(Orthonormal Matrix) 은 행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이루는 실수 행렬이다.
\[A A^T = A^T A = I\]위 조건을 만족하는 행렬이다.
다음과 같은 벡터 $\vec{u}, \vec{v}$ 의 내적값
\[\vec{u} = \begin{bmatrix} u_1 & u_2 & u_3 \end{bmatrix}, \vec{v} = \begin{bmatrix} v_1 & v_2 & v_3 \end{bmatrix} \\ \vec{u} \cdot \vec{v} = u_1 v_1 + u_2 v_2 + u_3 v_3\]백터를 행렬 곱셈으로 표현하면 아래와 같다.
\[\vec{u} \vec{v}^T = u_1 v_1 + u_2 v_2 + u_3 v_3\]유클리드 공간의 직교 란 내적이 0임을 뜻한다.
또한 두 행렬은 유클리드 공간의 정규 직교 기저를 이루는 행렬이라 할 수 있다.
벡터 $\vec{u}, \vec{v}, \vec{w}$ 로 이루어진 행렬 $A$ 가 있을 때
\[A = \begin{bmatrix} \cdots & \vec{u} & \cdots \\ \cdots & \vec{v} & \cdots \\ \cdots & \vec{w} & \cdots \end{bmatrix}, A^T = \begin{bmatrix} \vdots & \vdots & \vdots \\ \vec{u}^T & \vec{v}^T & \vec{w}^T \\ \vdots & \vdots & \vdots \end{bmatrix}\]이 둘을 행렬의 곱으로 연산한 결과가 내적은 0, norm 은 1이 되어야 한다는 뜻이다.
\[AA^T = \begin{bmatrix} \vec{u}\vec{u}^T & \vec{u}\vec{v}^T & \vec{u}\vec{w}^T \\ \vec{v}\vec{u}^T & \vec{v}\vec{v}^T & \vec{v}\vec{u}^T \\ \vec{w}\vec{u}^T & \vec{w}\vec{v}^T & \vec{w}\vec{w}^T \end{bmatrix} = I\] \[\|\vec{u}\| = \|\vec{v}\| = \|\vec{w}\| = 1\]이런 특징으로 정규직교행렬의 역행렬은 자신의 전치행렬이다.
(역행렬은 단위행렬을 만드는 행렬임으로)
직교행렬(Orthogonal Matrix) 정규직교행렬의 경우 전치와의 곱이 단위행렬을 유지하지만 직교행렬의 경우 대각행렬만 유지하면 된다.
자기수반행렬 (Hermitian Matrix)
정부호행렬(Definite matrix)
행렬간 연산
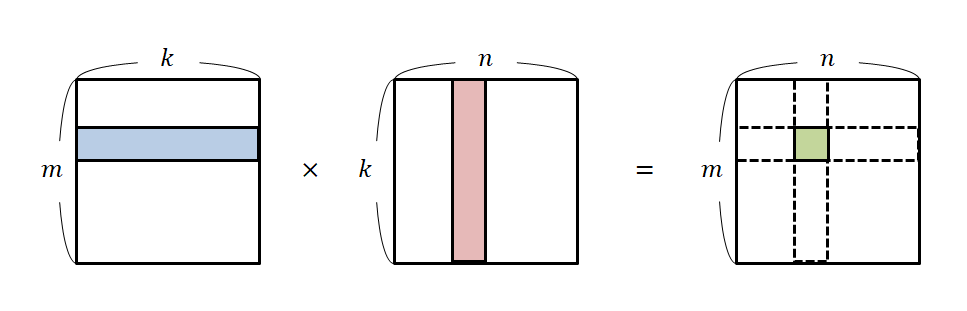
덧셈은 더할 두 행렬의 행과 열의 개수가 같아야 하고
곱셈은 곱할 두 행렬의 행은 열과, 열은 행과 같아야한다. axn 행렬이라면 nxb 행렬과만 곱할 수 있음
행과 열의 수가 다를경우 덧셈을 할 수 없다.
행렬에는 나누기는 존재하지 않는다.
단순 공식 외에 여러가지 관점으로 행렬의 곱셈을 생각할 수 있다.
출처:https://www.youtube.com/watch?v=Lo8FsB1anzQ&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=7
1. 방정식을 행렬로 표현
아래와 같이 똑같은 계수를 가진 일차방정식을 행렬로 표현할 수 있다.
\[\begin{cases} x_1 + 2y_1 = 4 & x_2 + 2y_2 = 3\\ 2x_1 + 5y_1 = 9 & 2x_2 + 5y_2 = 7 \end{cases}\] \[\begin{bmatrix} 1 & 2 \\ 2 & 5 \end{bmatrix} \begin{bmatrix} x_1 & x_2 \\ y_1 & y_2 \end{bmatrix} = \begin{bmatrix} 4 & 3 \\ 9 & 7 \end{bmatrix}\]2. 내적으로 행렬 포현
다음과 같이 행렬을 단순히 n 차원 백터 $\vec{a}$, $\vec{b}$ 로 표현하여 행렬의 곱셈을 표현할 수 있다.
\[A = \begin{bmatrix} \vec{a_1}^T \\ \vec{a_2}^T \\ \vec{a_3}^T \end{bmatrix}, B = \begin{bmatrix} \vec{b_1} & \vec{b_2} & \vec{b_3} \end{bmatrix}\]이는 사실 $\vec{a}, \vec{b}$ 의 내적이라 할 수 있다.
\[AB = \begin{bmatrix} \vec{a_1}^T \\ \vec{a_2}^T \\ \vec{a_3}^T \end{bmatrix} \begin{bmatrix} \vec{b_1} & \vec{b_2} & \vec{b_3} \end{bmatrix} = \begin{bmatrix} a_1^Tb_1 & a_1^Tb_2 & a_1^Tb_3 \\ a_2^Tb_1 & a_2^Tb_2 & a_2^Tb_3 \\ a_3^Tb_1 & a_3^Tb_2 & a_3^Tb_3 \end{bmatrix}\]3. rank-1 행렬의 합
\[AB = \begin{bmatrix} \vec{a_1} & \vec{a_2} & \vec{a_3} \end{bmatrix} \begin{bmatrix} \vec{b_1}^T \\ \vec{b_2}^T \\ \vec{b_3}^T \end{bmatrix} = a_1^Tb_1 + a_2^Tb_2 + a_3^Tb_3\]$\vec{a}$ 가 3x1 형태의 행렬
$\vec{b}$ 가 1x3 형태의 행렬
결국 3x3 형태의 행렬이 출력되어진다.
4. 열공간으로 나타내기
\[Ax = \begin{bmatrix} \vec{a_1} & \vec{a_2} & \vec{a_3} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \vec{a}_1x_1 + \vec{a}_2x_2 + \vec{a}_3x_3\]$A$ 는 3x3 행렬, $x$ 는 상수 3x1 형태의 열백터로 표현한것,
3x3 행렬을 3x1 백터로 곱하였으니 최종출력은 3x1 형태의 백터가 될 것이고
이는 즉 열벡터 3개(열공간) 으로 표현가능한 span 이라 할 수 있다.
이 span 내의 벡터 3개를 다시 모아 또다른 행렬로 나타낼 수도 있을 것이다.
마찬가지로 행공간으로도 span 를 구성하고 다시 다른 행렬로 조합할 수 있다.
행공간(row space), 열공간(column space)
행공간(row space) 은 m x n 행렬의 행백터들의 선형변환으로 구성 가능한 집합, 즉 행 백터들의 span 이다.
반대로 열공간(column space) 는 열 백터들의 span 이라 할 수 있다.
아래와 같은 행렬 $A$ 가 있을 때
\[A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{21} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\]아래와 같이 행을 기반으로 $r_1 \cdots r_m$ 으로 나눠서 행공간 $R(A)$ 를 표현가능
\[r_1 = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \end{bmatrix} \\ r_2 = \begin{bmatrix} a_{21} & a_{22} & \cdots & a_{2n} \end{bmatrix} \\ \vdots \\ r_m = \begin{bmatrix} a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \\ \ \\ R(A) = \mathrm{span} \{r_1, r_2, \cdots, r_m \}\]아래와 같이 열을 기반으로 $c_1 \cdots c_n$ 으로 나눠서 열공간 $C(A)$ 를 표현가능
\[c_1 = \begin{bmatrix} a_{11} \\ a_{21} \\ \cdots \\ a_{m1} \end{bmatrix} \ c_2 = \begin{bmatrix} a_{12} \\ a_{22} \\ \cdots \\ a_{m2} \end{bmatrix} \ \cdots \ c_n = \begin{bmatrix} a_{1n} \\ a_{2n} \\ \cdots \\ a_{mn} \end{bmatrix} \\ \ \\ C(A) = \mathrm{span} \{c_1, c_2, \cdots, c_n \}\]영공간(null space)
영공간(null space) 은 아래 그림과 같이 선형변환후에 $(0,0)$ 으로 모이는 벡터들의 span을 뜻한다.
$Ax = 0$ 를 만족하는 $x$ 의 집합
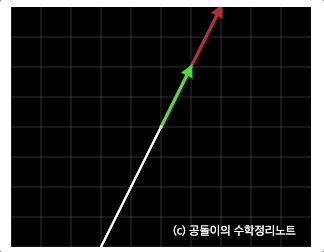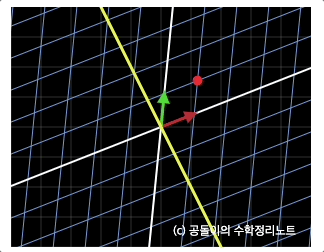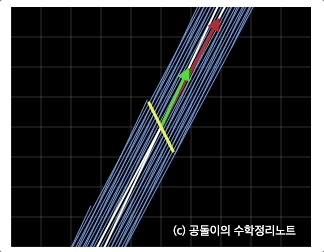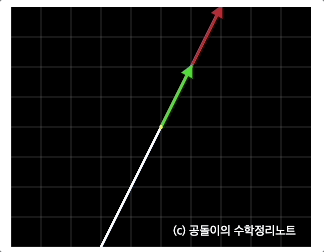
출처: https://angeloyeo.github.io/2020/11/17/four_fundamental_subspaces.html
그림처럼 열백터가 평행해 열공간이 1차원 직석일 경우 영공간은 원점으로부터 직교하는 직선상의 모든 벡터가된다.
3차원 행렬 2x3 형태의 행렬 $A$ 를 에로들면
2x3 형태의 행렬을 곱해야 하니 $x$ 는 3x1 형태의 열백터일 것
결과가 [0,0] 이 되려면 $x$ 의 값은 다음과 같을 수 있다.
$x$ 의 모든 요소가 0 일 경우 영행렬이 출력되는 것은 당연한 일이고
[-2,1,0] 혹은 [-3,0,1] 형태의 상수배 열백터는 모두 곱한 결과가 0이 나온다.
따라서 $x$ 의 집합은 아래와 같이 정의할 수 있다.
\[x_n = c_1 \begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix}\] \[x_m = c_2 \begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}\] \[A(c_1x_n) = A(c_2x_m) = 0\]여기에 나아가서 두 x 집합의 선형결합 역시 0이 출력된다.
\[x_n = c_1 \begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix} + c_2 \begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}\] \[A(c_1x_ n + c_2x_m) = 0\]$x_n, x_m$ 으로 표현할 수 있는 span 이 모두 0으로 변환되기에 해당 span(평면) 을 모두 영공간이라 할 수 있다.
영공간과 내적
영공간의 정의가 $Ax = 0$ 를 만족하는 $x$ 의 집합 이었는데
이는 행렬 $A$ 를 행공간으로 전개하고 열백터 $x$ 와 내적했을 때 결과값이 0일 때
즉 $A$ 의 모든 행백터와 $x$ 를 내적했을 때 수직인 것과 같다.
반대로 $x^T$ 와 $A$ 의 모든 열백터를 내적했을 때 수직인것도 영공간이라 할 수 있는데
이때의 $x_n$ 의 집합은 left null space 라 한다.
영공간의 차원
위 예제의 경우 영공간 차원은 2차원이라 할 수 있으며 수식으로 아래와 같다.
\[\dim(N(A)) = 2\]영공간의 차원은 특이한 법칙이 있는데
rank 수 와 $\dim(N(A))$ 를 더하면 column 수 이다.
행렬 $A$ 가 m x n 형태라면 아래와 같이 영공간 차원수를 정의할 수 있다.
반대로 행렬 $A$ 의 left null space 의 영공간 차원수는
행렬의 행공간, 열공간, 영공간의 관계를 그림으로 표현하면 아래와 같다.
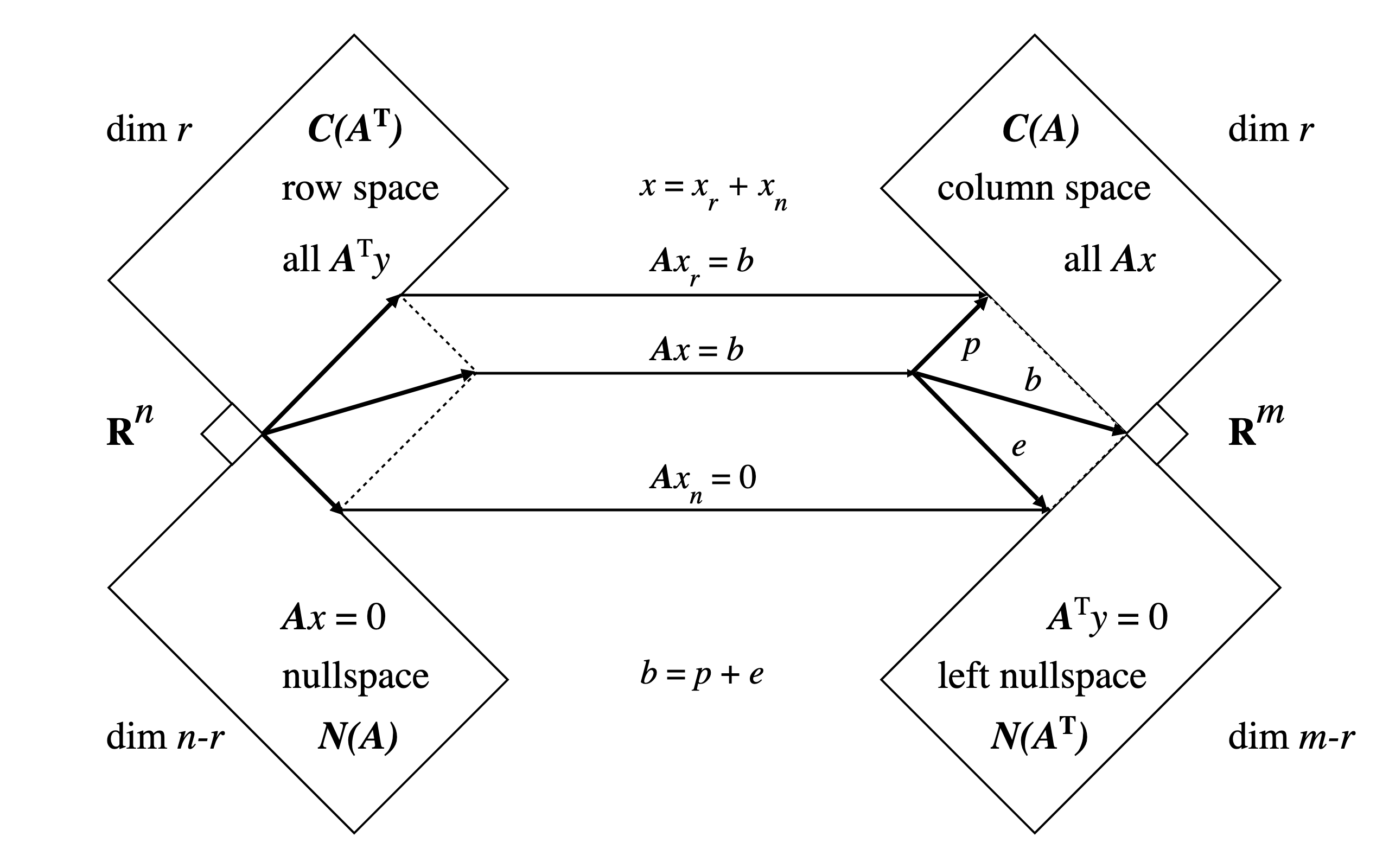
row space 의 $x_r$ 에 A 를 곱하면 column