백터
백터는 n차원 좌표에서의 0점에서 $x_1, x_2, \cdots, x_n$ 좌표까지의 숫자의 나열이다.
보동 벡터라 하면 열벡터를 뜻하고 행백터를 사용할 땐 별로도 전치표기를 붙여 사용한다.
\[\vec{v} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\] \[\vec{v}^T = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\]주로 2차원 에서 $x, y$ 기호를 사용하여 숫자와 화살표를 사용해 사용하지만
백터의 정의는 숫자의 나열이다.
내적 (內積 inner product, dot product, scalar product)
內積: 안으로 쌓다
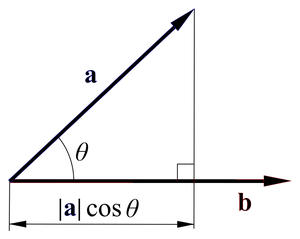
내적을 기하학적으로 표기하면 아래 그림과 같다.
- 벡터 두 개를 하나의 스칼라 값으로 변환시키는
- 한 벡터의 방향으로 나머지 하나를 projection(투영) 시키는
두 벡터의 각 성분끼리의 곱의 합이다.
\[\vec{a} \cdot \vec{b} = |\vec{a}| \cos\theta |\vec{b}| = a_1b_1 + a_2b_2\]$\cos$ 공식을 사용해 아래처럼 증명
\[\begin{aligned} \vec{a} \cdot \vec{b} &= |\vec{a}| \cos\theta |\vec{b}| \\ &= \sqrt{a_1^2 + a_2^2} \times \frac{a_1b_1+a_2b_2}{\sqrt{a_1^2 + a_2^2} \times \sqrt{b_1^2 + b_2^2}} \times \sqrt{b_1^2 + b_2^2} \\ &= a_1b_1+a_2b_2 \end{aligned}\]삼차원 좌표계에서도 내적을 구하는 공식은 똑같다. \(\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3\)
내적은 유사도를 구하는 문제에서 많이 쓰이는데 $\vec{a}$ 와 $\vec{b}$ 의 내적값이 두 벡터의 스칼라와 차이가 많이 없다면,
두 벡터는 서로 유사하다고 할 수 있다.
백터의 내적
선형대수학에서 내적은 dot product 로 말하며 수식도 $\cos\theta$ 보다는 행렬의 곱으로 표현한다.
\[\vec{a} \cdot \vec{b} = a^Tb = a_1b_1 + a_2b_2\]스칼라값이기 때문에 $a^Tb = b^Ta$ 연산 순서도 상관없다.
백터의 크기를 구할 때 내적을 사용하여 표현한다.
\[\sqrt{a^Ta}\]크기가 1인 벡터를 단위백터(unit vector) 라 하는데 단위백터도 내적을 사용하여 표현한다.
벡터의 정규화(Normalization) 라고 한다.
스칼라값이 아닌 내적된 백터(정사영된 벡터)를 구하려면
정사영된 크기가 $ \vert \vec{a} \vert \cos\theta $ 임으로 해당 스칼라에 정사영한 벡터의 방향의 단위백터만 곱해주면 된다.
위 그림의 $\vec{a}$ 가 $\vec{b}$ 에 내적되는 것을 예로들면 아래와 같다.
\[| a | \cos\theta \frac{b}{\sqrt{b^Tb}} \\ \ \\ = \sqrt{a_1^2 + a_2^2} \times \frac{a_1b_1+a_2b_2}{\sqrt{a_1^2 + a_2^2} \times \sqrt{b_1^2 + b_2^2}} \times \frac{b}{\sqrt{b_1^2 + b_2^2}} \\ \ \\ = \frac{a_1b_1 + a_2b_2}{b_1^2+b_2^2} \times b \\ \ \\ = \frac{a^Tb}{b^Tb}b\]기하학적으로 생각하면 $b$ 백터에 정사영된 백터는
$b$ 백터에서 상수배만큼 줄어들었다 생각할 수 있으니 $b\hat{x}$ 로 표현 가능하고
정사영된 백터로부터 $a$ 백터로 수직되는 백터는 $a - \vec{b}\hat{x}$ 로 표현할 수 있다.
$b\hat{x}$ 와 $a - \vec{b}\hat{x}$ 는 서로 수직임으로 내적하면 0이되고
$\hat{x}$ 를 도출할 수 있다.
방향 도함수(directional derivative)
내적은 정사영된 벡터 방향으로의 순간변화율 이라고도 표현할 수 있다.
\[\vec{x} \cdot \vec{u}\]$\vec{u}$ 방향으로의 $\vec{x}$ 의 순간변화율
외적 (外積 outer product, cross product)
외적을 기하학적으로 표기하면 아래 그림과 같다.
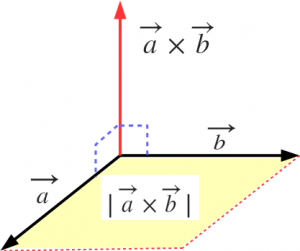
외적은 3차원 공간에서 두 백터가 이루는 평행사변형의 면적의 크기만큼 수직되는 방향으로 쏘는 또다른 백터(법선) 를 구하는 것이다.
3차원 좌표계에서 외적을 구하려면 행렬식이 필요하다.
\[\vec{a} \times \vec{b} = \det( \begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{bmatrix}) = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1)\]내적과 외적은 이름만 비슷할 뿐 서로 관련이 없다.
외적은 기하문제에서 주로 사용된다.
직선의 벡터 방정식
벡터와 평행하는 직선의 방정식
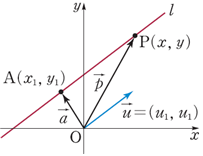
실수 $t$ 배의 $\vec{u}$ 와 $\vec{a}$ 를 더하면 $\vec{P}$ 가 나온다 할 수 있다.
\[\vec{P} = \vec{a} + t \vec{u}\]$x, y$ 관계식으로 바꾸면 아래와 같은데
\[\begin{aligned} (x,y) &= (x_1, y_1) + t(u_1, u_2) \\ &= (x_1 + t u_1, y_1 + t u_2) \end{aligned} \\ \ \\ \begin{cases} x = x_1 + tu_1 \\ y = y_1 + tu_2 \end{cases}\] \[t =\frac{x-x_1}{u_1}, t =\frac{y-y_1}{u_2} \\ y - y_1 = \frac{u_2}{u_1} (x - x_1)\]최종적으로 아래같은 직선의 방정식을 출력할 수 있다.
\[y = \frac{u_2}{u_1} (x - x_1) + y_1\]벡터와 수직되는 직선의 방정식
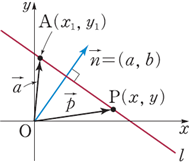
그림처럼 법선벡터 $\vec{n}$ 과 좌표 $A(x_1, y_1)$ 이 주어졌을 때
아래와 같이 내적공식으로부터 수직되는 직선의 방정식을 유도할 수 있다.
Norm
백터에서의 Norm은 길이를 뜻하고
백터에서 Norm은 아래와 같이 표현
일반적으로 2차원으로 표시함으로 아래 식을 자주 사용
\[\|v\| = \sqrt{a^2+b^2}\]백터 역시 n 차원일 수 있음
\[\|W\| = \sqrt{w_1^2 + w_2^2 + \cdots + w_n^2} = \sqrt{W^TW}\]P Norm
\[\|W\|_p = \left( \sum_i | W_I |^p \right)^\frac{1}{p}\]일반적으로 Norm 하면 위의 $p=2$ 인 L2 Norm 을 뜻한다.
\[\|W\|_2 = \left( \sum_i | W_I |^2 \right)^\frac{1}{2} = \sqrt{w_1^2 + w_2^2 + \cdots + w_n^2} = \sqrt{W^TW}\]$p=1$ 절대값의 합
$p=2$ Euclideam Norm, L2 Norm
$p=\infty$ 요소중 가장 큰값에 가까워진다
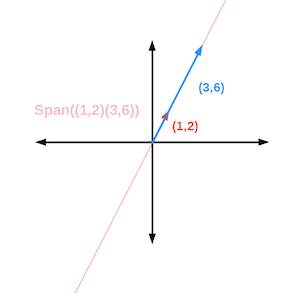
Span
span은 모든 Linear Comination(선형결합) 의 집합이다
선협결합은 아래와 같이 상수 $a$ 와 백터 $\vec{v}$ 의 결합이라 할 수 있으며
\[a_1\vec{v_1} + a_2\vec{v_2} + \cdots + a_n\vec{v_n}\]span 은 이렇게 선형결합된 백터들로 표현할 수 있는 영역(vector space by linear combination) 을 뜻한다.
vector space 라 말하기도 함
아래와 같이 기저벡터 $\vec{v},\vec{w}$ 의 span 은 2차원평면 전체라 할 수 있다.
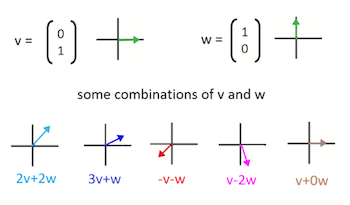
반면에 서로 수평되는 백터들은 아무리 선형결합을 해도 span 이 그 수평선을 넘어가지 않는다.