개요
삼각함수는 각에따라 생겨나는 삼각형의 여러 값들을 논하는 함수이지만
이해를 위해 단위원을 기반으로 자주 설명한다.
sine(sin): 활현tangent(tan): tangent line(접선)secant(sec): cut, 자르다
그림을 보면
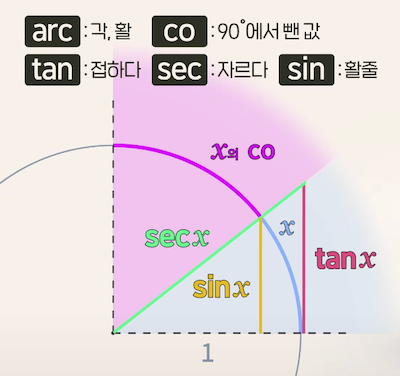
$\sin$ 은 활 시위형태 $\sec$ 는 원을 자르고 $\tan$ 는 원에 접한다
$\mathrm{arc}\sin \frac{1}{2}$ 는 $\sin\frac{1}{2}$ 의 각이 얼마인지 물어보는 함수
$\sin$ 값이 $\frac{1}{2}$ 이 될 각은 $30^\circ$ 이기에 호도법으로 표기하면 $\frac{\pi}{6}$ 이다.
\[\mathrm{arc}\sin \frac{1}{2}=\frac{\pi}{6}\]co 의 뜻
기존 $\sin, \sec, \tan$ 함수를 보조하려고 생긴 함수로 $\mathrm{co}$ 는 $90^\circ$ 에서 뺀값을 듯한다.
$\mathrm{cos - cosine}$
$\mathrm{cot - cotangent}$
$\mathrm{csc - cosecant}$
$90^\circ$ 도 중 반대편각을 $x$ 로 둔다면 기존 $\sin, \sec, \tan$ 앞에 $\mathrm{co}$ 만 붙여주면 된다.
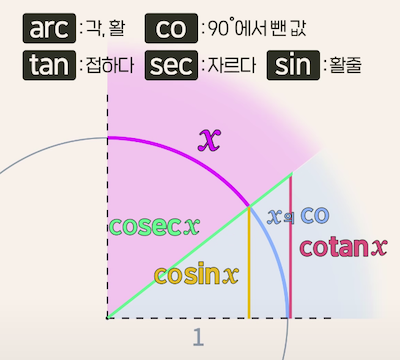
한눈에 보면 아래 그림과 같다.
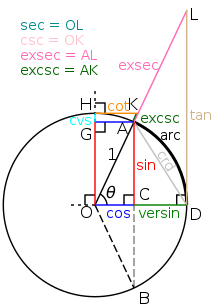
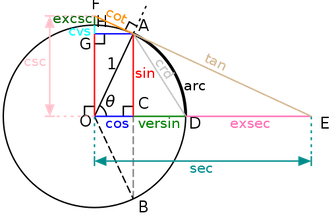
특징
삼각함수의 대부분 공식 및 특징은 은 피타고라스 정리로 설명가능하다.
$\tan$ 특징
$\tan$ 는 기울기로 사용가능한데 $\mathtt{기울기 = \frac{수직값}{수평값}}$ 이기 때문
밑변이 1이기 때문에 수평값은 1, 수직값은 $\tan x$ 이다.
기울기 값은 $(x, y)$ 로 표현한 좌표계에서 $\frac{y}{x}$ 라 할 수 있다.
여기서 $x=\cos\theta, y=\sin\theta$ 로 표기할 수 있기 때문에 아래 식처럼 고쳐쓸 수 있다.
$a^2 + b^2 = c^2$ 공식에 의해 $1^2 + \tan^2x = \sec^2x$
\[\sec^2x = 1 + \tan^2x \\ \ \\ \sec^2x - \tan^2x = 1\]$\csc$ 와 $\cot$ 도 마찬가지
\[\csc^2x = 1 + \cot^2x \\ \ \\ \csc^2x - \cot^2x = 1\]삼각함수 관계식
사실 반지름 $r=1$ 이기에 간단하게 연산할 수 있는것이지
단위원의 접한 부분을 $(x,y)$ 로 표기했을 때 실제 삼각함수를 표현하는 수식은 아래와 같다.
$\sin\theta = \frac{y}{r}$
$\sec\theta = \frac{1}{\cos\theta}$
$\tan\theta = \frac{x}{y}$
$\sec\theta = \frac{1}{\cos\theta}$
$\csc\theta = \frac{1}{\sin\theta}$
$\cot\theta = \frac{1}{\tan\theta}$
$\theta > 90^\circ(\frac{\pi}{4})$ 일 경우에
90 으로 나눈 나머지 부분의 삼각비를 구한 후 1 ~ 4 분면에 따른 $x, y$ 음수부호만 추가하여 계산해주면 된다.