미분 개요
미분계수
$x$ 의 변화량이 매우 작을 때 기울기
극한값이 존재할 때 함수 $f(x)$ 의 순간변화율을 미분계수라 함
순간변화율(instant rate of change) = 미분계수(differencetial coefficient)
$\frac{y변화량}{x변화량} = {\frac{y_1-y_2}{x_1-x_2}} = 기울기 = 미분계수$
이런 미분계수를 구하기 위한 함수를 도함수라 한다.
\[f'(x)\] \[\frac{dy}{dx}\] \[\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}\] \[\lim_{h \to 0}\frac{f(x+h) - f(x)}{h}\]모두 미분계수를 구하기 위한 식이다.
$\frac{dy}{dx}$ 는 분수가 아닌 극소한 $x$ 의 변화량 대비 $y$ 의 변화량을 뜻하는 단순 기호
자연상수 e
자연상수 $e$ 는 미분에서 특이한 성질을 가진다.
대다수의 미분공식이 자연상수 $e$, 그리고 자영상수 $e$ 의 극한과 연관이 있어 알아두어야 한다.
$e$ 의 정의는 아래와 같다.
\[e = \lim_{h\to0}(1+h)^{\frac{1}{h}} = 2.718...\]$h=\frac{1}{x}$ 로 치환하면 아래식으로도 표현 가능
(역수임으로 $x\to \infty$)
또 다른식으로 아래처럼도 표기가능하다.
\[e = \sum_{k=0}^\infty \frac{1}{k!} = 2.718...\]$\log_e x$ 를 자연로그라 하며 $\ln x$ 라고 간략하게 표기한다.
자연상수 극한
자연상수 $e$ 를 사용한 특이한 공식이 있다.
\[\lim_{h\to0} \frac{e^h-1}{h} = 1\]$e^h - 1 = t$ 로 치환하였을 때
$h = \ln(1+t)$ 로 표기할 수 있다.
또한 $e^h - 1 = t$ 임으로 $h \to 0$ 일경우 $t \to 0$ 이다.
위의 치환식을 공식에 대입하면 아래와 같다.
\[\lim_{h\to0} \frac{e^h-1}{h} = \lim_{t\to0} \frac{t}{\ln(1+t)}\]그리고 $\frac{1}{t}$ 로 분모, 분자에 곱해준다.
\[\begin{aligned} & \lim_{t\to0} \frac{t}{\ln(1+t)} \\ &= \lim_{t\to0} \frac{1}{\frac{1}{t}\ln(1+t)} \\ &= \lim_{t\to0} \frac{1}{\ln(1+t)^\frac{1}{t}} \end{aligned}\]분모의 형식을 보니 자연상수 e의 공식과 매우 닮아있다.
\[e = \lim_{t\to0}(1+t)^{\frac{1}{t}}\]그래서 위 공식을 또 아래처럼 변경 가능하다.
\[\begin{aligned} & \lim_{t\to0} \frac{1}{\ln(1+t)^\frac{1}{t}} \\ &= \lim_{t\to0} \frac{1}{\ln e} \\ &= 1 \end{aligned}\]또 자연상수로부터 아래식도 유도 가능하다.
\[\begin{aligned} \lim_{x\to 0} (1+x)^{\frac{1}{x}} &= e \\ \lim_{x\to 0} \ln(1+x)^{\frac{1}{x}} &= \ln e = 1 \\ \lim_{x\to 0} \frac{1}{x} \ln(1+x) &= 1 \\ \end{aligned}\]미분공식
$(f(x) + g(x))’ = f’(x) + g’(x)$
$(f(x)g(x))’ = f(x)g’(x) + f’(x)g(x)$
$ (\frac{f(x)}{g(x)})’ = \frac{g(x)f’(x) - f(x)g’(x)}{g(x)^2} $
$g’(f(x)) = g’(f(x)) \ f’(x)$
다항함수의 미분공식
$f(x) = x^n$ 일때 도함수는 $f’(x) = nx^{n-1}$
자연수 $x$ 에 대해 증명은 아래와 같다.
\[\begin{aligned} & \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\ &= \lim_{h \to 0} \frac{(x+h)^n - x^n}{h} \\ &= \lim_{h \to 0} \frac{x^n + _nC_1x^{n-1}h^1 + _nC_2x^{n-2}h^2 + ... + _nC_nh^n - x^n}{h} \\ &= \lim_{h \to 0} (_nC_1x^{n-1} + _nC_2x^{n-2}h + ... + _nC_nh^{n-1}) \\ &= nx^{n-1} \end{aligned}\]맨앞과 끝의 $x^n$ 은 서로 지워지고
이항정리와 $h$ 의 약분, 살아남은 식들은 $h\to0$ 이기에 다 0으로 수렴하여
결국 $_nC_1x^{n-1} = nx^{n-1}$ 만 남는다.
위는 자연수에서의 증명이지만 실수에서도 위 공식은 성립한다.
아래 로그함수 미분을 사용하면 실수에서도 증명이 가능하다.
$(\ln x)’ = \frac{1}{x}$ 임으로 $ln|y|’ = \frac{n}{x}$

지수함수 미분
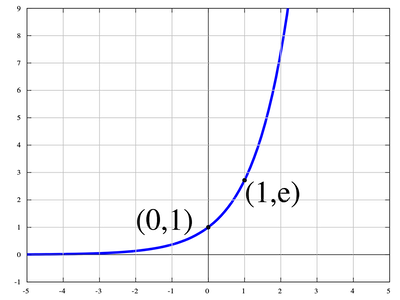
$f’(x) = (e^x)’ = e^x$
$e$ 지수함수는 기존 함수와 도함수가 똑같다.
위에서 구한 자연상수e 의 공식 $\lim_{h\to0} \frac{e^h-1}{h} = 1$ 으로 인해 최종적으로 아래처럼 변경된다.
\[\begin{aligned} &\lim_{h\to0}\frac{e^{x+h} - e^x}{h} \\ &= \lim_{h\to0}\frac{e^x(e^h-1)}{h} \\ &= \lim_{h\to0}e^x \times 1 \\ &= e^x \end{aligned}\]$a^x$ 미분을 구하는 공식은 아래와 같다.
\[\begin{aligned} &\lim_{h \to 0} \frac{a^{x+h} - a^x}{h} \\ &= \lim_{h \to 0} \frac{a^x(a^h-1)}{h} \\ &= a^x\lim_{h \to 0} \frac{a^h-1}{h} \end{aligned}\]여기서 $\lim_{h \to 0} \frac{a^h-1}{h} = \ln a$ 임으로
$f’(x) = (a^x)’ = a^x \ln a$ 가 성립
로그함수 미분
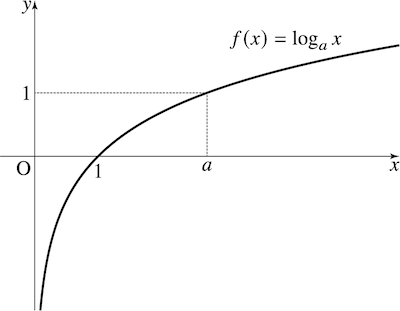
로그함수의 도함수는 자연로그함수의 도함수로부터 추출 가능
\[\begin{aligned} &\lim_{h \to 0} \frac{\ln(x+h) - \ln(x)}{h} \\ &=\lim_{h \to 0} \frac{1}{h} \ln(\frac{x+h}{x}) \\ &=\lim_{h \to 0} \frac{1}{h} \ln(1 + \frac{h}{x}) \\ &=\frac{1}{x} \lim_{h \to 0} \frac{x}{h} \ln(1 + \frac{h}{x}) \\ \end{aligned}\]여기서 $\frac{h}{x} = t$ 로 치환, $h \to 0$ 일때 $t \to 0$ 이다.
\[\frac{1}{x} \lim_{t \to 0} \frac{1}{t} \ln(1 + t) \\\]어디서 많이 본 식인데 자연상수로부터 유도된식과 비슷하다
\[\lim_{x\to 0} \frac{1}{x} \ln(1+x) = 1\]그래서 $\frac{1}{x}$ 뒤의 식은 1로 수렴하기에 아래 미분공식이 성립한다.
\[f'(x) = (\ln x) = \frac{1}{x}\]$\ln$ 이 아닌 $\log_a$ 로 미분해보자.
\[\frac{\ln x}{\ln a} = \log_a x\] \[(\log_a x)' = (\frac{\ln x}{\ln a})' = \frac{1}{\ln a} (\ln x)'\]상수는 분리버리고 $(\ln x)’$ 는 $\frac{1}{x}$ 임으로
기존에 있던 $\frac{1}{\ln a}$ 만 곱해주면 아래식이 나온다.
적분
간단히 말하자면 적분은 아래 그림과 같이
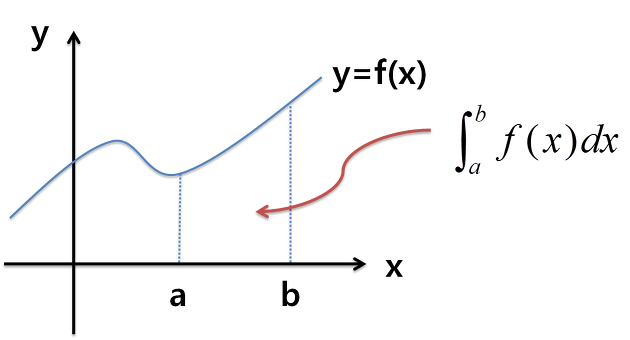
직교좌표계에서 사용할 경우 면적을 구하기 위한 계산방식이다.
$F(x)$ 를 미분하여 $f(x)$ 가 된다면,
즉 $F’(x) = f(x)$ 라면
$F(x)$ 는 $f(x)$ 의 원시함수(primitive function) 이다.
이 원시함수를 알아야 적분공식을 통해 면적을 알 수 있다.
$y=x^2$ 이차함수 에서 $x=1$ 에서 $x=2$ 까지의 면적을 구해보자.
먼저 $x^2$ 의 원시함수를 구해야한다.
$(\frac{x^3}{3})’ = x^2$
$F = (\frac{x^3}{3})$
\[\int_1^2f(x)dx = [F(x)]_1^2 = F(2) - F(1) = \frac{2^3}{3} - \frac{1^3}{3} = \frac{7}{3}\]따라서 면적은 $\frac{7}{3}$ 이 된다.
이렇게 범위가 명확이 $a,b$ 혹은 $1,2$ 처럼 정해져 있는 적분을 정적분
범위가 정해져 있지 않고 $-\infty \to \infty$ 적분을 부정적분 이라 한다.
구분구적법
위에서 단순 공식으로 $\int_a^b f(x) dx$ 로 a 부터 b 까지의 면적을 표기했지만 사실 아래 그림과 같이 무수히 많은 직사각형의 면적의 합이라 할 수 있다.
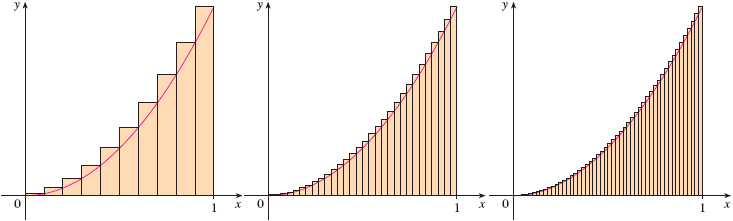
이 합을 $\sum$ 공식으로 표기할 수 있는데 바로 구분구적법이다.
$n$ 은 직사각형의 개수
$\frac{b-a}{n}$ 은 직사각형의 밑변길이라 할 수 있다.
$k$ 번째 직사각형의 면적은 높이-$f(a + \frac{b-a}{n}k)$ 넓이-$\frac{b-a}{n}$ 임으로
\[f(a + \frac{b-a}{n}k) \cdot \frac{b-a}{n}\]그래서 모든 $k$ 개의 직사각형의 $\sum$ 를 구하면 구분구적법 완성
\[\int_a^b f(x) dx = \lim_{n\to\infty} \frac{b-a}{n} \sum^n_{k=1} f(a + \frac{b-a}{n}k)\]이상적분
이상적분: 부적절한 적분(improper integral)
종점이 명확하지 않는경우 종점이 무한대로 이어지거나 불연속 함수일 경우
극한을 사용하여 넓이는 구하는 방식을 이상적분이라 한다.
무한한 넓이이기에 발산할것 같지만 수렴하는 경우가 있다.
\[\int_1^\infty \frac{1}{x^2}dx = \lim_{b\to\infty}\int_1^b \frac{1}{x^2}\]이는 정적분으로 다시 나타낼 수 있따.
\(\lim_{b\to\infty} [-\frac{1}{x}]_1^b = \lim_{b\to\infty}-\frac{1}{b}+1=1\)
즉 넓이는 1로 수렴하게 된다.
\[\int_0^1 \frac{1}{x}dx = \lim_{b\to 0}\int_b^1 \frac{1}{x}dx\]