Dimension Reduction (차원축소)

차원축소를 통해 데이터가 눈에 보이게(Observable) 측정(measure) 할 수 있다.

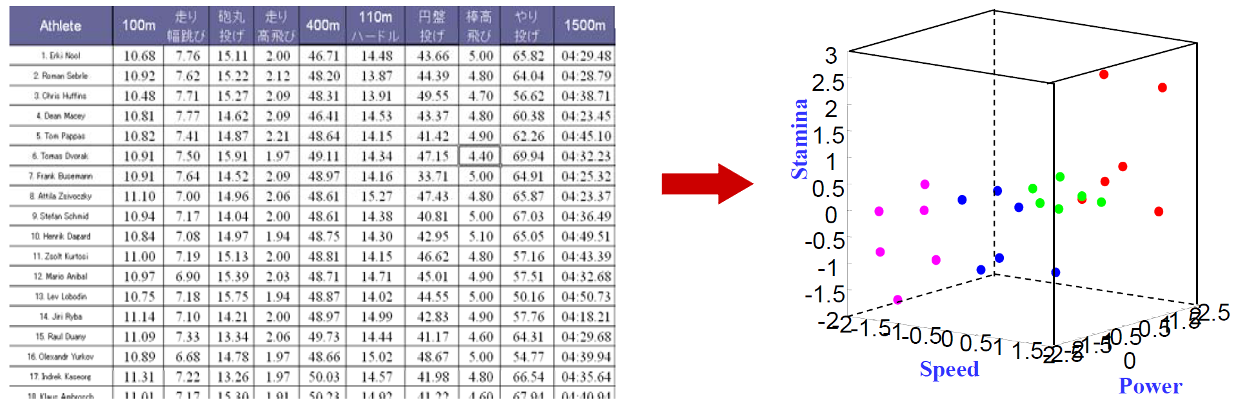
위 달리기 기록 차원(칼럼)이 10이 넘는데 3차원(힘, 속도, 스테미너)으로 visualization 할 수 있을까? 아래에서 소개하는 여러 접근방법으로 차원축소 방법을 지원한다.

가장 대표적인 차원 축소 방법론으로 PCA, ISOMAP 등이 있다.

대부분의 차원축소 방법론은 상관관계(Correlation matrix) 가 높은 변수들을 묶어서 처리하는
공분산(Covariance matrix) 개념을 사용한다.

Covariance Matrix(공분산 행렬)

공분산 행렬의 기하학적 의미는 아래 사진과 같다.

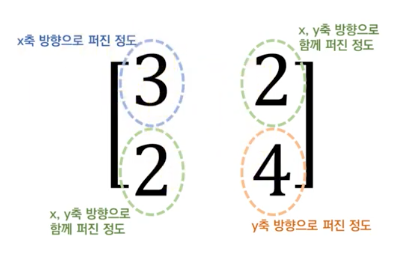
해당 행렬과 데이터(백터) 를 곱해 선형변환을 해주면

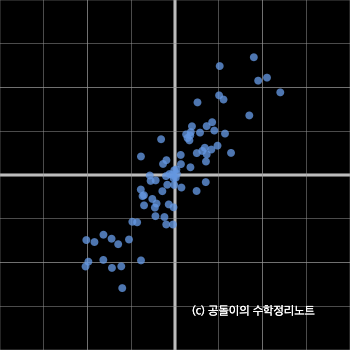
위처럼 공모양의 데이터가 공분산 행렬 값에 의해 펼쳐지게 된다.

공분산 구하기

수식으로 표현하면 아래와 같다.

$n \times d$ 로 구성된 행렬 $X$ 가 있다.

$n$ 는 데이터의 개수(row)
$d$ 는 속성의 개수(feature)

키와 몸무게를 예로 들면 아래와 같은 열백터 2개로 이루어진 행렬이 존재할 것이다.

\[\begin{bmatrix} 170 & 70 \\ 150 & 45 \\ 160 & 55 \\ 180 & 60 \\ 172 & 80 \end{bmatrix}\]

해당 데이터를 바로 쓰지 않고 보통 feature 의 각 데이터의 속성별 mean(평균) 값을 빼서 사용한다

\[X = D - mean(D) = \begin{bmatrix} 170 & 70 \\ 150 & 45 \\ 160 & 55 \\ 180 & 60 \\ 172 & 80 \end{bmatrix} - \begin{bmatrix} 166 & 62 \\ 166 & 62 \\ 166 & 62 \\ 166 & 62 \\ 166 & 62 \end{bmatrix} = \begin{bmatrix} 4 & 8 \\ -16 & -17 \\ -6 & -7 \\ 14 & -2 \\ 6 & 18 \end{bmatrix}\]

즉 feature 의 편차들만 모아 다시 열백터로 구성한것
이 값들을 가지고 공분산 행렬을 구할 수 있다.

\[\sum = \frac{1}{n} X^TX\]

위 그림을 보면 속성의 편차들을 모은 백터를 서로 내적시킨다.

대각선에 있는 내적값은 같은 편차집합백터를 내적(제곱)한 것이기에 feature의 분산값이다.

\[X^TX = \begin{bmatrix} 4 & -16 & -6 & 14 & 6 \\ 8 & -17 & -7 & -2 & 18 \end{bmatrix} \begin{bmatrix} 4 & 8 \\ -16 & -17 \\ -6 & -7 \\ 14 & -2 \\ 6 & 18 \end{bmatrix} = \begin{bmatrix} 540 &426 \\ 426 & 730 \end{bmatrix}\]

PCA (Principal Component Analysis: 주요 구성 요소 분석)

아래같은 n차원 데이터를 일차원으로 변경할 수 있을까?

분포에 따른 함수축을 만들면서 2차원적으로 어느정도 떨어져 있는지는 알수 없게되지만,
어떤 길이에 데이터가 몰려있는지 더 단순하게 알수 있게된다.

중요한(주요 구성) 데이터만을 사용하기에 데이터 로스는 생기지만 단순함과 효율성은 증가한다.

차원의 수가 너무 많아 데이터 분석이 어렵다면 가장 큰 특성을 가지는 feature 만을 가지고 분석하겠다는 차원 축소 방법론이다.

예로 국어점수, 영어점수가 있는 2차원 데이터를 1차원 직선으로 분석하고 싶다면
우리가 가장 nomal 하게 생각할 수 있는 것은 국어점수와 영어점수를 더해 평균을 내는것.

만약 시험 난이도에 따라 가중치를 부여하할 수 도있을것이다.

아래 사진의 경우 빨간선이 모두 같은 가중치를 부여했을때 평균을 내는 선
파란선이 각 점수에 영어에 0.6, 수학에 0.4 가중치를 줄 경우 나타내는 선

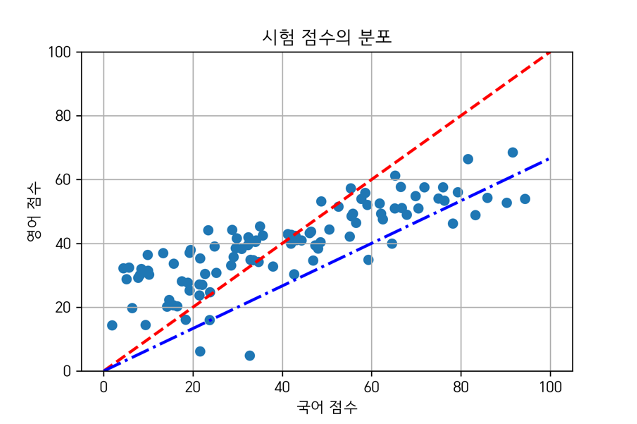
만약 점수를 그래프상의 백터로 나타낸다면 백터의 projection 으로도 볼 수 있다.

projection, 특정 방향으로의 단위백터와 내적

$(국어점수, 영어점수) \cdot (가중치1, 가중치2)$

우리의 목표는 데이터를 백터에 정사영 했을때 가장 큰 분산값을 가질 수 있는 백터를 찾는 것이다.

projection 하기위한 그래프로 평균그래프나 가중치 그래프는 좋지 못하다.
현재 그래프는 중심축이 0,0 우측 상방 에 모든 데이터가 출력되는 형식인데 데이터들의 중간에 중심축을 가지는 벡터를 찾는것이 가장 좋은 방법일 것이다. 아니면 데이터를 중심축쪽으로 끌어 내리던가

뭐가 되었든 데이터 구조를 바꾸기 위해선 공분산 행렬을 사용해야 한다.

ISOMAP

nonlinear dimensionality reduction method: 비선형적 차원 감소 함수

isometric: 등축 투영법 이라는 3차월 물체는 2차원 그림으로 표현할 때 사용하는 기법, 중고등학교에서 정육면체 그릴때 자주 사용함. 대부분의 데이터는 2차원같이 단순한 형식의 선형적으로 표현할 수 없다.

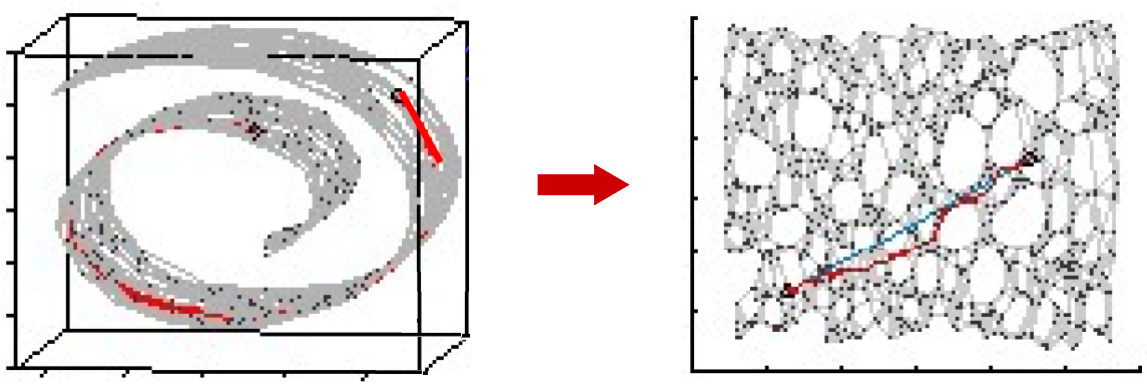
위와 같은 양피지처럼 생긴 3차원 정보를 2차원 정보로 변경할때 고려해야 할 점은 여러가지다 위와 같은 경우 대표적으로 고려할 점은 Local Distance, Euclidean Distance 이다. Local Distance 는 양피지를 폈을때 점과 점의 거리 Euclidean Distance 는 단순 좌표 x1,y1,z1 과 x2,y2,z2 의 거리라 할 수 있다.
위 그림에서 변환된 2차원 데이터는 Local Distance를 기반으로 고려해 변환한 것이다.

Descriptive Analytics 에서 사용하는 분석기법의 목적은 대부분 데이터의 설명 혹은 전처리에 관한 내용이다.