Transformer

https://www.youtube.com/watch?v=mxGCEWOxfe8
https://wikidocs.net/31379
http://jalammar.github.io/illustrated-transformer/ https://arxiv.org/abs/1706.03762

Attention 모델은 모든 은닉 상태 $hs$ 를 사용하면서 높은 성능을 보여줬는데
여전히 RNN을 사용하는 모델이다 보니 학습이 느리고, 고질적인 문제인 기울기 폭발 혹은 기울기 소실 문제가 발생한다.

RNN 특성상 시각의 순서에 따라 연산이 이루어지다 보니 병렬연산이 불가능해 학습이 느리다.

이때문에 RNN 을 사용하지 않고 Attention 기법만으로 사용하는 모델이 Transformer 이다.

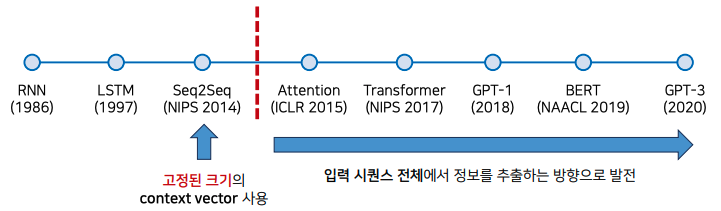
Transformer 을 기점으로 자연어처리에서 더이상 RNN 을 사용하지 않고 Attention 기법만을 사용한다.

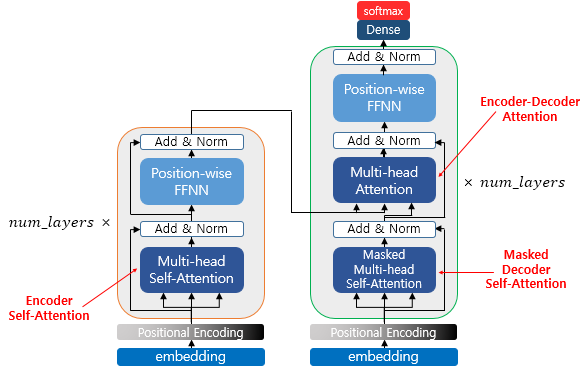
Transformer 모델그림은 아래와 같이 인코더와 디코더 2개로 나뉘며 3가지 종류의 Attention 이 있는데 하나씩 알아볼 예정

Encoder

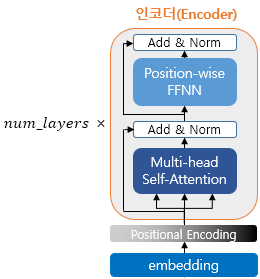
인코더는 크게 아래와 같이 나눌 수 있다.

• Input Embedding
• Multi head Attention(Encoder self attention)
• Add & Norm(Residual Learning)
• Position wise FFNN

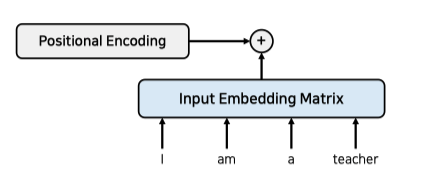
Input Embedding

각 단어에 대한 Embedding Vector 를 사용하기 위해 Input Embedding Matrix 를 정의하고
RNN 처럼 순서에 대한 처리를 위해 단어별 위치정보값인 Positional Encoding 값을 더해준다.

입력단어들을 한번에 Encoder 에 넣어 병렬연산이 가능하다.

\[\begin{aligned} PE_{(pos, 2i)} &= \sin(pos/10000^{2i/d_{model}}) \\ PE_{(pos, 2i+1)} &= \cos(pos/10000^{2i/d_{model}}) \end{aligned}\]

여기서 $[d_{model}, pos, i]$ 값은 아래 참고

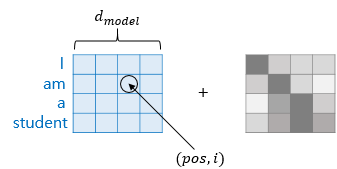
Positional Encoding 을 위한 행렬값을 연산해 두고 위치정보값으로 사용한다.
값은 항상 -1 ~ 1 사이의 값이고

Multi head Attention(Encoder self attention)

기존 Attention 모델에선 Encoder 의 은닉상태들을 모아 $hs$ 를 구성하고
Decoder 의 은닉상태와 내적을 통해 Attention Score 를 구했었다.

하지만 Transformer Encoder 에선 입력된 단어들끼리 Attenction Score 를 구한다.
그래서 self-attention 이라 부른다.

그림과 같이 Encoder 의 Multi head Attention 에 3가지 벡터 $Q, K, V$ 가 input 으로 들어가는데
Embedding Vector 에 Positional Encoding 된 값을 행렬과 Linear 연산한 것이다.

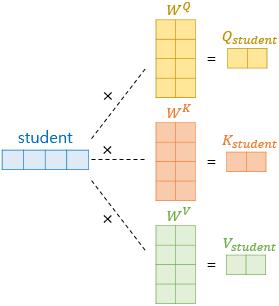
즉 동일한 Embedding Vector 가 가중치 $W^Q, W^K, W^V$ 에 의해서 $Q, K, V$ 로 출력되고 Multi head Attention input 으로 들어간다.

행렬곱 연산이다보니 아래와 같이 입력된 Embedding Vector 를 한번에 연산한 수 있다.

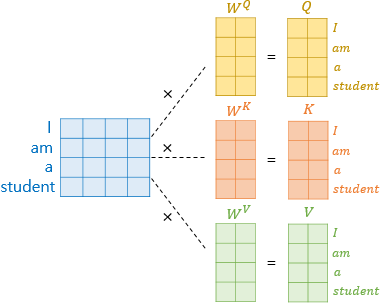
그리고 Multi head 란 이름처럼 가중치 $W^Q, W^K, W^V$ 는 head 의 개수만큼 존재한다.

논문에선 8개를 사용했다.

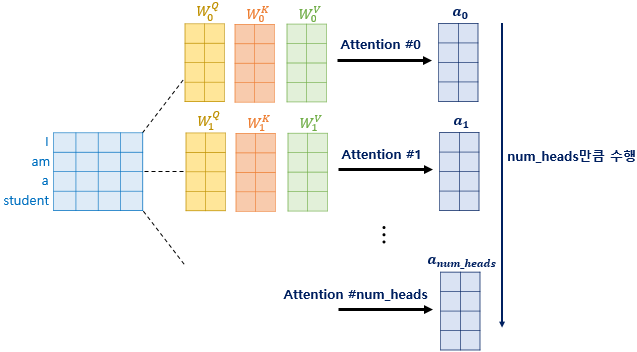
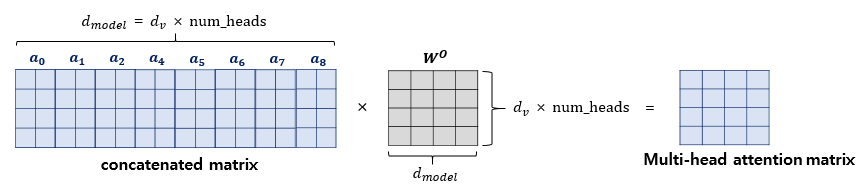
출력된 여러개의 Attention Value 들은 concat 되어 가중치 $W^o$ 와 linear 연산을 거치고
하나의 Multi head Attention 이 종료된다.

Multi head Attention 과 Add & Norm(아래에서 소개) 과정은 layer 수 만큼 반복하고
각 layer 의 가중치들은 모두 별개의 값들이다.

논문에선 layer 수를 6개로 설정하여 인코더 층을 구성했다.

Scaled Dot Product Attention

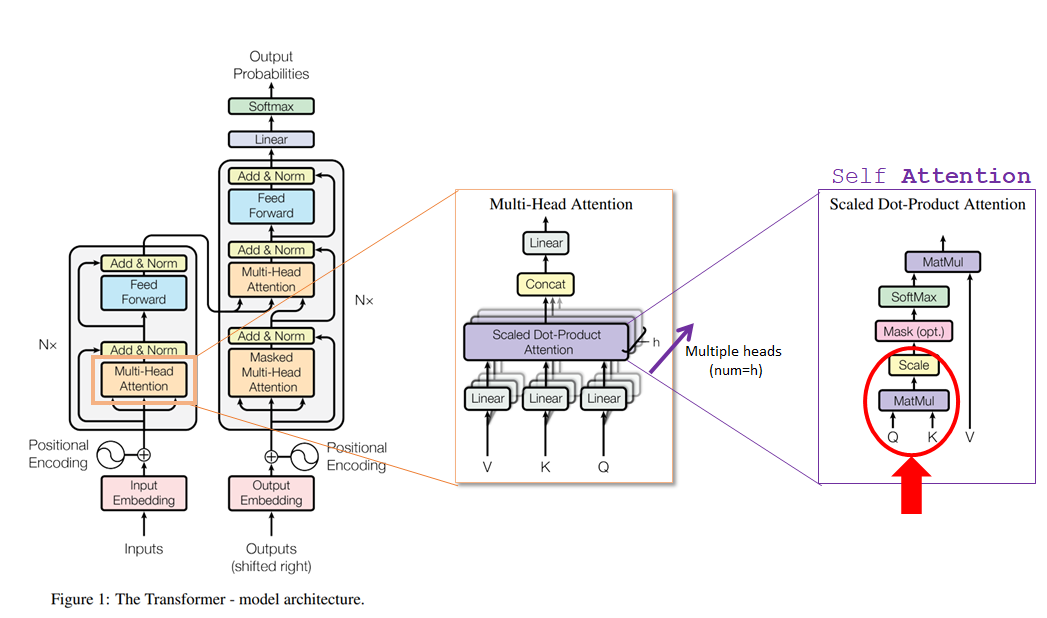
Multi head Attention 내부 Scaled Dot Product Attention 은 아래와 같다.
여기서부턴 기존의 Attention 모델과 비슷한 방향으로 흘러간다.

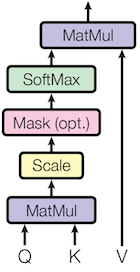
$Q, K$ 를 행렬곱(MatMul) 하면 Attention Score 가 출력된다.
$Q, K$ 모두 같은 입력에서 $W^Q, W^K$ 를 통해 출력된 값인데 자기들(self) 끼리 행렬곱을 진행한다.

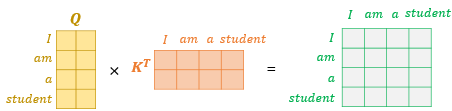
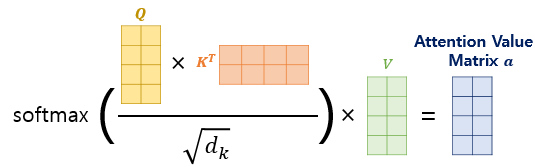
그리고 $\sqrt{d_k}$ 로 Scale 하고 Softmax 하면 Attention Distribution 가 출력되고 가중치로 사용한다.
이 가중치에 의해 $V$ 의 특정 행벡터를 희미해지고, 특정 행벡터는 진해질것이다.
이렇게 가중치에 의해 변화된 $V$ 를 Attention Value 로 사용한다.

여기서 설명하지 않은 부분이 Mask(optional) 인데, 아래와 같이 <pad> 를 행렬에 추가하는 것이다.

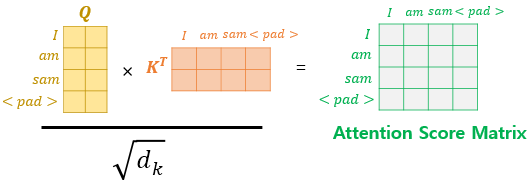
<pad> 에 0이 아닌 값이 설정되어 있다면 해당 열, 해당 행은 모두 마스킹한다.

Add & Norm(Residual connection)

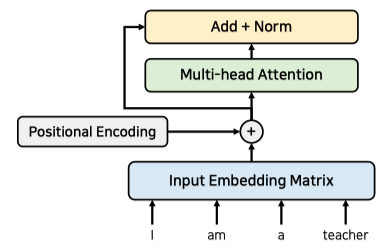
Resnet 과 같이 Residual connection 기법을 사용하기 때문에
Multi head Attention 변경이전의 데이터 Add 하여 학습데이터로 사용한다.

정규화 과정은 아래와 같이 각 행벡터의 평균, 분산값을 구한 후

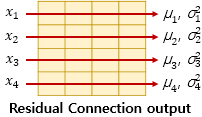
각 행렬 요소값에 아래와 같은 연산을 취해 정규화 한다.

\[\hat{x}_{i,k} = \frac{x_{i,k} - \mu_i}{\sqrt{\sigma^2_i + \epsilon}}\]

$\epsilon$ 은 분모가 0 되는것을 방지하기 위한 작은값

여기에 편향과 비슷하게 사용되는 2개의 벡터 $\gamma, \beta$ 를 사용한다.
초기값은 각각 1과 0이다.

\[\gamma = [1, 1, \cdots, 1] \\ \beta = [0, 0, \cdots, 0] \\\]

최종적으로 아래와 같이 정규화과정이 이루어지고 $\gamma, \beta$ 는 학습들 통해 변화한다.

\[\mathrm{LayerNorm}(x_{i}) = \gamma \hat{x}_i + \beta\]

Position wise FFNN(feedforward neural network)

Fully connected Layer 라 볼 수 있다.
$x$ 는 Multi head Attention 과 Add & Norm 를 통해 출력된 값.

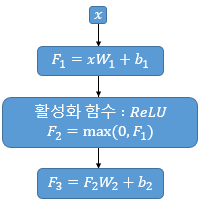
Position wise FFNN 에는 아래 2개의 가중치가 존재한다.

\[W_1(d_{model}, d_{ff}) \\ W_2(d_{ff}, d_{model})\]

논문에서 사용한 $d_{model}$ 은 512, $d_{ff}$ 는 하이퍼파라미터로 2048 을 사용한다.

Decoder

보통 Decoder layer 개수도 Encoder layer 개수만큼 있음

Encoder 는 모든 단어에 대해 Attention 연산을 수행함으로 양방향 연산이 이루어진다.
Deocder 는 순차적으로 입력된 단어에 대해 Attention 연산을 수행함으로 전체적으로 보면 단방향 연산이라 할 수 있다.

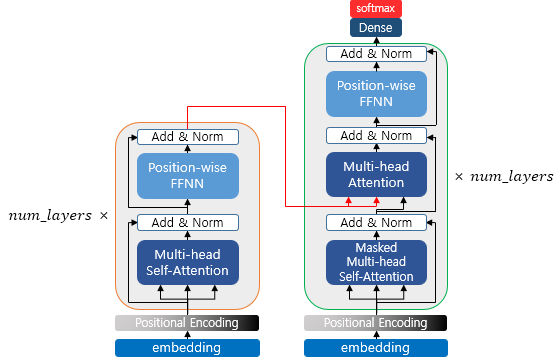
디코더는 크게 아래와 같이 나눌 수 있다.

• Output Embedding
• Masked Multi head Attention(Self Attention)
• Multi Head Attention(Encoder Decoder Attention)
• Add & Norm(Residual Learning)
• Position wise FFNN
• Final Linear and Softmax Layer

여기서 Encoder 에서 설명하지 않은 아래 3개 구성요소에 대해서 설명한다.

• Output Embedding
• Masked Multi head Attention(Self Attention)
• Multi Head Attention(Encoder Decoder Attention)

Output Embedding

Encoder 에서는 한번에 Embedding Vector 를 넣었지만
Decoder 에서는 그럴수 없다.

아래 그림처럼 seq2seq 와 비슷하게 이전 시간에 출력된 단어를 다음 입력 Embedding Vector 로 사용한다.

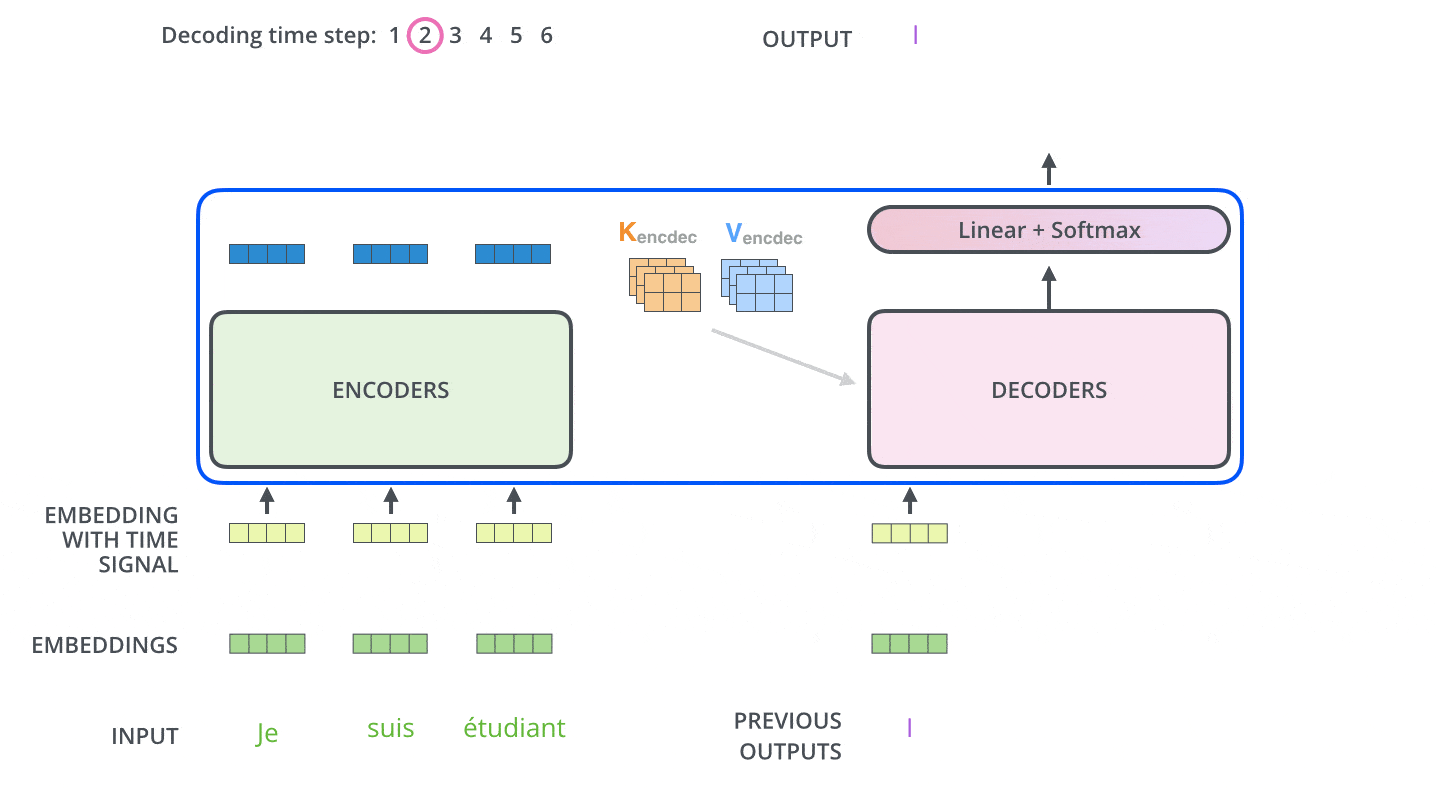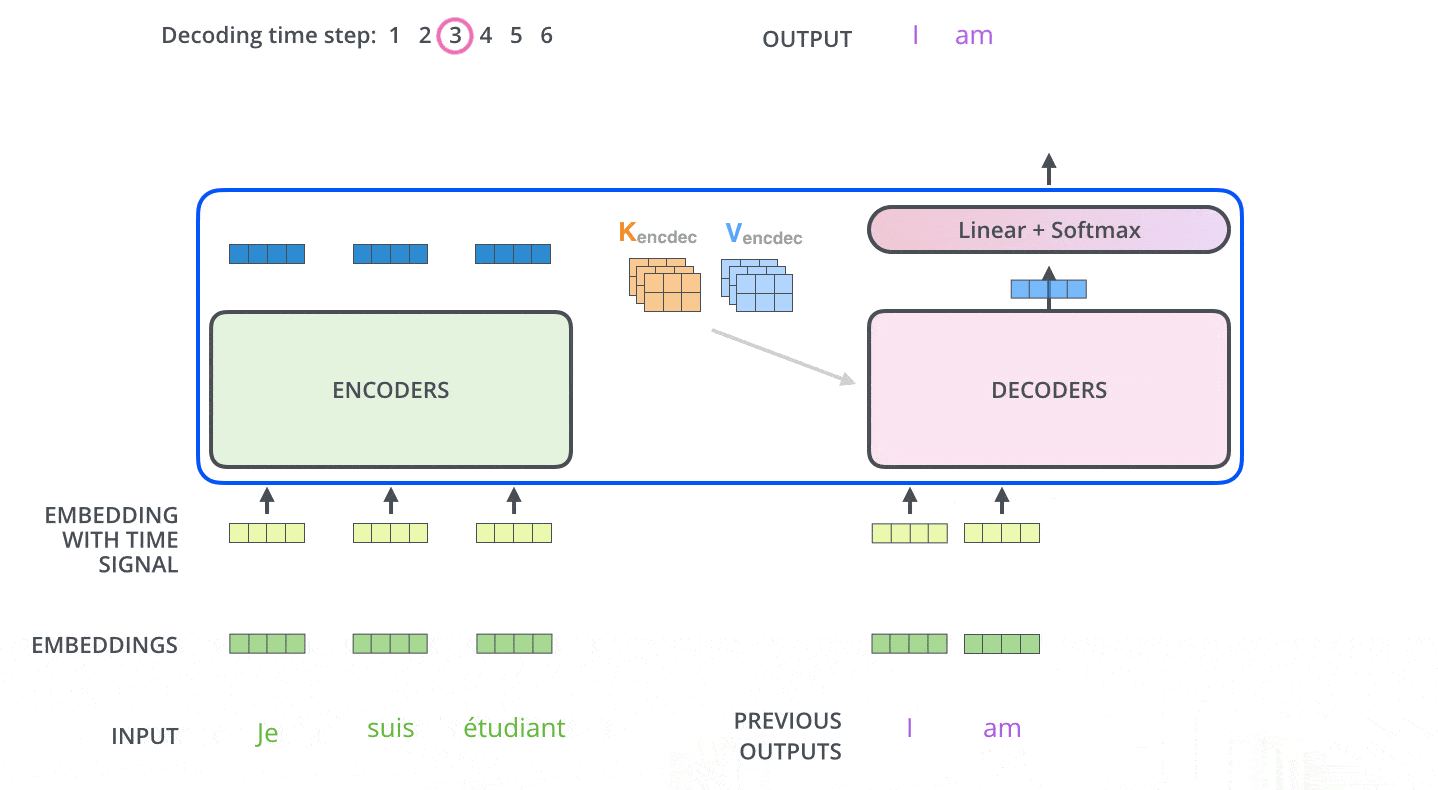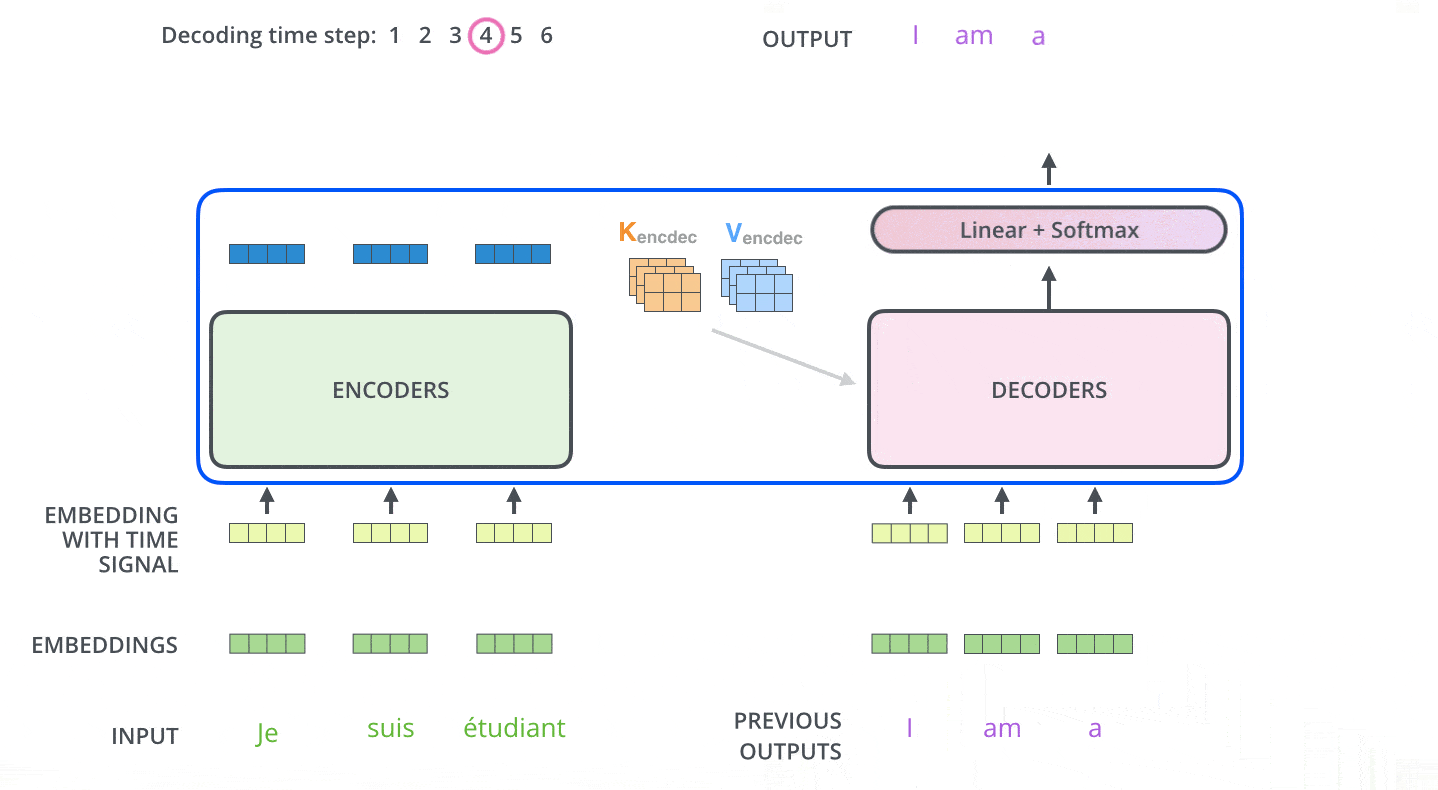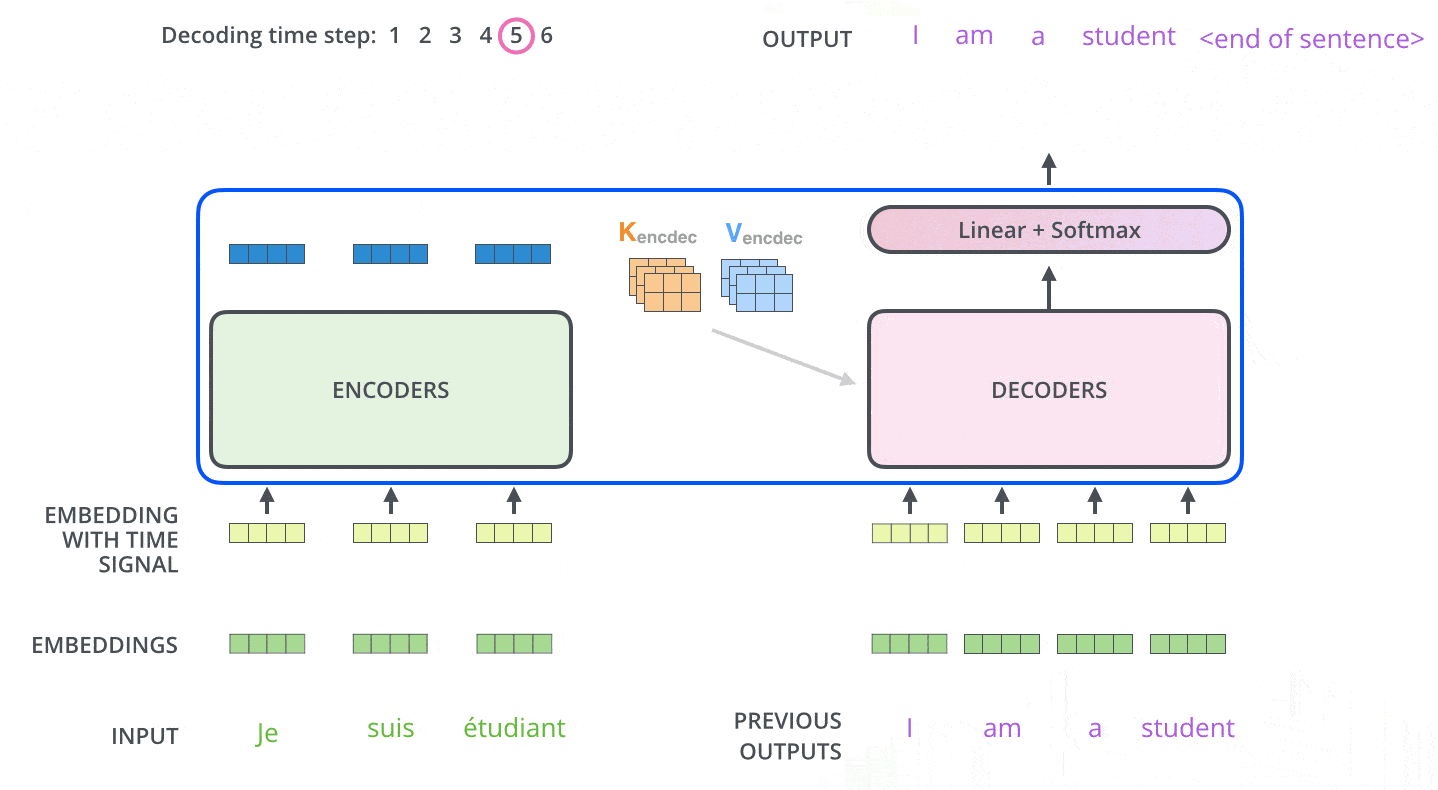
Teacher Force Training

학습시에는 seq2seq 학습방법과 똑같이 학습시에는 출력한 문장에 해당하는 단어 행렬을 한번에 입력하는 Teacher Force Training 기법을 사용한다.

하지만 RNN 을 사용하는 seq2seq 와 다르게 Transformer 모델은 입력한 Embedding Vector 배열들 간 Attention 연산을 하다보니 첫번째 Embedding Vector 가 미래 출력될 Embedding Vector 와 헹렬곱 연산을 해버리게 된다.

그렇기에 학습시에는 아래와 같이 정답 Embedding Vector 행렬에 Attnetion Score 를 구한 값에
look-ahead mask 를 도입해 미래에 있는 단어들은 참고하지 못하도록 마스킹한다.

Multi Head Attention

Decoder 에는 2종류의 Multi Head Attention 이 존재한다.

• Masked Self Attention
• Encoder Decoder Attention

첫번째로 만나는 Masked Self Attention 의 경우 look-ahead mask 처리한 Attention Score 를 입력받는다 하여 Masked Multi head Attention 이라 부른다.

Masked Multi head Attention 는 Encoder 의 Multi head Attention 처럼 초기 입력되는 Embedding Vector $Q, K, V$ 값이 동일하다(가중치만 다를뿐).

두번째로 만나는 Encoder Decoder Attention 의 경우 Encoder 의 마지막 레이어의 출력값을 받아 Multi Head Attention 에 사용한다.

Query : 디코더 행렬
Key = Value : 인코더 행렬