추론기반 기법
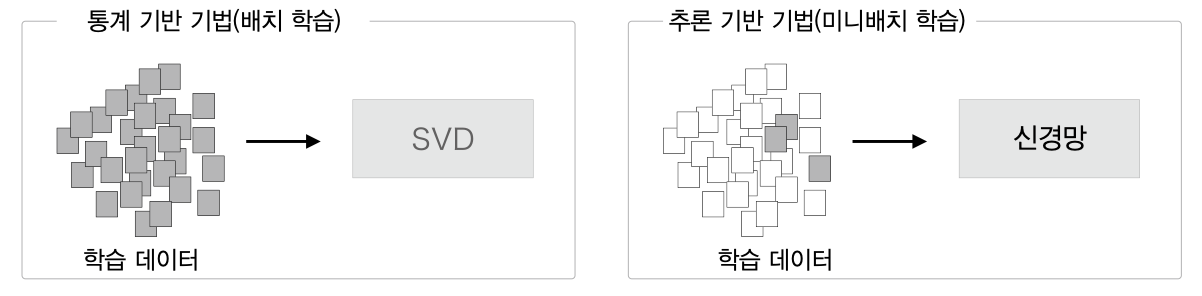
위에서도 말했듯이 통계기반 기법은 단어의 개수가 많을수록 거대한 단어 백터 행렬을 만들게 된다.
때문에 최근에는 더 많은 데이터를 학습데이터로 삼아 학습할 수 있도록 신경망을 사용한 추론 기반 기법 을 사용한다.
그녀석 무슨 배짱인지 ___ 로 와서 일을 하겠다고 한다.
삽이라도 있어야 땅을 파지 ___ 로야 어떻게 하겠나.
SO만 있으면 코딩은 ___ 로도 할 수 있다고 한다.
가운데 마스킹된 단어는 '맨손' 이다.
결국 단어의 결정은 우리가 문맥(context) 라 부르는 주변 단어로부터 결정되는 것이고
이러한 방식이 추론기반 기법이다.
원핫 벡터
원핫 벡터는 원핫 표현이라고도 함
원핫 벡터는 단순히 단어 인덱스 위치의 원소를 1, 나머지는 0 으로 설정하는 방식이다.
You say goodbye and I say hello
위 문장의 단어중 You, goodbye 를 원핫백터 로 표시하면 아래 그림과 같다.
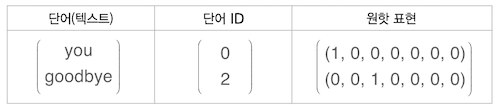
어쨋든 단어를 백터로 바꿨고 이를 단어의 word2vec 라 할 수 있다.
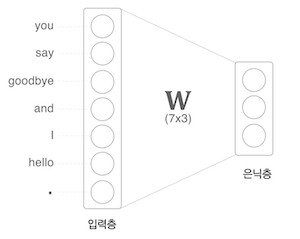
코드로 구현하면 아래와 같다.
import numpy as np
c = np.array([[1, 0, 0, 0, 0, 0, 0]]) # 입력
W = np.random.randn(7, 3) # 가중치
h = np.matmul(c, W) # 은닉층의 중간노드
print (h)
# [[-0.70012195 0.25204755 -0.79774592]]
원핫 벡터의 문제는 여러가지다.
- 단어 개수가 많아질 수 록 메모리 문제가 발생
- 벡터값중 0 이 압도적으로 많기 때문에 희소표현(Sparse Representation) 문제가 발생
또한 원핫벡터는 단순 위치정보이다 보니 단어의 유사도를 보존하지 않는다.
Word2Vec
이런 문제가 있다보니 웟핫 벡터 말고 단어를 벡터로 표현하는 다른 방법을 찾아야 했다.
원핫 벡터의 문제점을 해결하기 위해 아래와 같은 조건을 만족해야 한다.
- 밀집표현(Dense Representation) 을 사용하는 방식
- 메모리 문제 해결을 위한 벡터차원 고정
밀집표현: 벡터 대부분 0대신 실수값으로 구성됨, 희소표현(Sparse Representation) 의 반의어
워드 임베딩(word embedding): 단어 간 의미적 유사성을 벡터화하는 작업
임베팅 벡터(embedding vector): 밀집표현으로 구성된 벡터를 뜻함
원핫벡터의 경우 대부분이 0이고 일부만 1인 희소표현이다.
단어 벡터 간 유의미한 유사도를 반영할 수 있도록 단어의 의미를 수치화 할 수 있는 방법이 필요한데
이런 문제점을 해결한 것이 Word2Vec 방식이다.
모든 단어에 카테고리를 지정해 학습실킬 순 없으니 문장 단위로 각 단어들과의 관계를 기반으로 학습하는 것이 대부분이다.
그럼 사용되는 각 단어의 정보를 일정된 크기의 숫자(벡터)로 표기할 수 있다.
기본이 되는 대표적인 방법은 아래 2가지
CBOW모델은 주변 단어를 활용해 중간에 있는 단어를 예측한다.Skip-Gram모델은 현재 단어를 활용해 주변에 있는 단어를 예측한다.
CBOW (continuous bag-of-words)
CBOW 모델은 입력된 단어의 주변단어(context) 를 사용하여 가장 연관성을 가지는 단어를 추측하는 용도의 신경망으로 직역하면 지속 단어장 이라 할 수 있다.
예를 들어 아래 문장 중 say 를 중간값, 참고할 주변단어 개수 N=1 로 설정하여,
양옆의 you, goodbye 를 주변단어로 학습데이터를 구축할 경우 아래 그림과 같다.
You say goodbye and I say hello
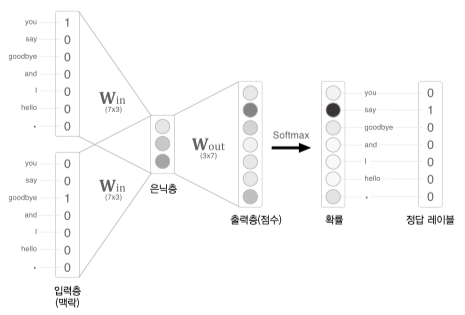
그림의 경우 2개 단어에 대한 단어백터를 $W_{in}, W_{out}, \mathrm{Softmax}$ 함수를 거쳐 가장 연관있는 단어를 추론하게 된다.
여기선 예제표현을 위해 원핫 백터를 사용했지만 다른 정수인코딩을 통해 출력된 단어 백터를 사용하는 것이 정석
만약 주변단어를 더 많이 설정하고 싶어 W$_{in}$ 에서 출력되는 단어의 값을 $h1, h2$ 라 표현 하면
은닉층이 입력받는 값은 두 값의 평균이다. $\frac{1}{2}(h_1 + h_2)$
출력층은 $W_{out}$ (3x7) 행렬곱으로 출력된 7 차원 백터로 각 단어의 점수 를 뜻하며 단어간의 연관성을 표현하는 백터로 사용한다.
최종적으로 you 와 goodbye 단어 2개를 넣고 가장 연관성 있는 단어가 say 로 추론되어야 한다는 의미이다.
아래는 say 를 중간값, 주변단어개수 N=2 로 설정했을 때 간략화한 그림이다.
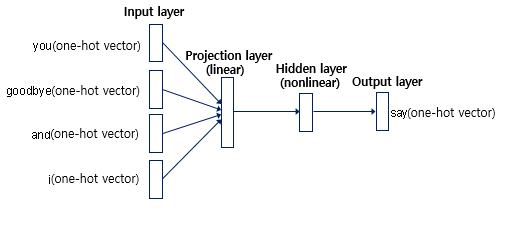
어쨋든 우리의 목표는 단어들을 Word Embedding vector(Word2Vec) 로 만드는 것
여기서 은닉층에 해당하는 layer 를 projection layer 라 하는데(첫 그림의 경우 3x1)
projection layer 를 say 란 중심단어의 대한 밀집표현 백터라 할 수 있다.
학습이 완료되었을 때 이 Projection layer 의 벡터값을 Word Embedding vector 라 할 수 있겠다.
처음 학습에는 원핫 벡터를 학습값, 예측값으로 사용했지만
다음부턴 학습된 Projection layer 로 사용 가능하다.
CBOW 학습
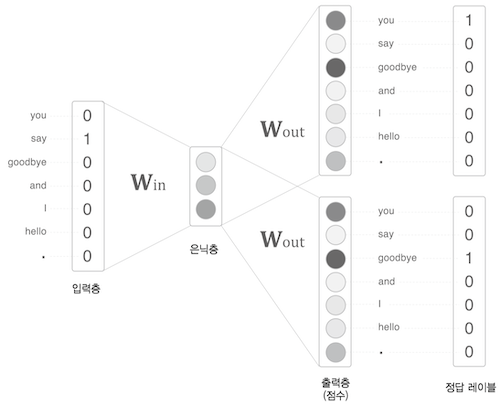
말뭉치에 대한 학습 데이터는 아래 사진처럼 구성한다(2개의 단어에 대한 원핫백터를 넣은이유)
양옆의 단어(context)를 입력값으로 선택하고 타깃 단어가 출력될 수 있는 모델을 생성하는것이 목표이다.

위 그림을 보면 you, goodbye 두 단어와 가장 연관선 있는 단어는 say 이다.
정답 레이블 또한 say 의 원핫 벡터로 지정한 후 학습을 진행한다.
학습은 일반적인 Cross Entropy Error 계층을 사용하여 완전결합 계층의 가중치인 $W_{in}, W_{out}$ 들을 조절한다.
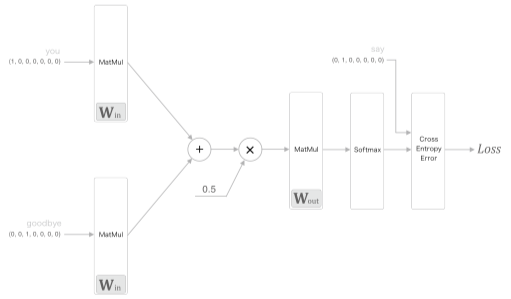
일반적인 딥러닝학습에서는 모든 가중치를 학습대상에 포함되지만 대부분 연구에서 입력 가중치 $W_{in}$ 만을 사용한다.
# coding: utf-8
import sys
sys.path.append('..')
import numpy as np
from common.layers import MatMul, SoftmaxWithLoss
class SimpleCBOW:
def __init__(self, vocab_size, hidden_size):
V, H = vocab_size, hidden_size
# 가중치 초기화
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(H, V).astype('f')
# 계층 생성
self.in_layer0 = MatMul(W_in)
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
self.loss_layer = SoftmaxWithLoss()
# 모든 가중치와 기울기를 리스트에 모은다.
layers = [self.in_layer0, self.in_layer1, self.out_layer]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# 인스턴스 변수에 단어의 분산 표현을 저장한다.
self.word_vecs = W_in
def forward(self, contexts, target):
h0 = self.in_layer0.forward(contexts[:, 0])
h1 = self.in_layer1.forward(contexts[:, 1])
h = (h0 + h1) * 0.5
score = self.out_layer.forward(h)
loss = self.loss_layer.forward(score, target)
return loss
def backward(self, dout=1):
ds = self.loss_layer.backward(dout)
da = self.out_layer.backward(ds)
da *= 0.5
self.in_layer1.backward(da)
self.in_layer0.backward(da)
return None
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmax의 출력
self.t = None # 정답 레이블
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 정답 레이블이 원핫 벡터일 경우 정답의 인덱스로 변환
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx
목표는 가장 손실값이 적은 $W_{in}$ 행렬을 구하는 것
역전파를 그림으로 표현하면 아래와 같다.
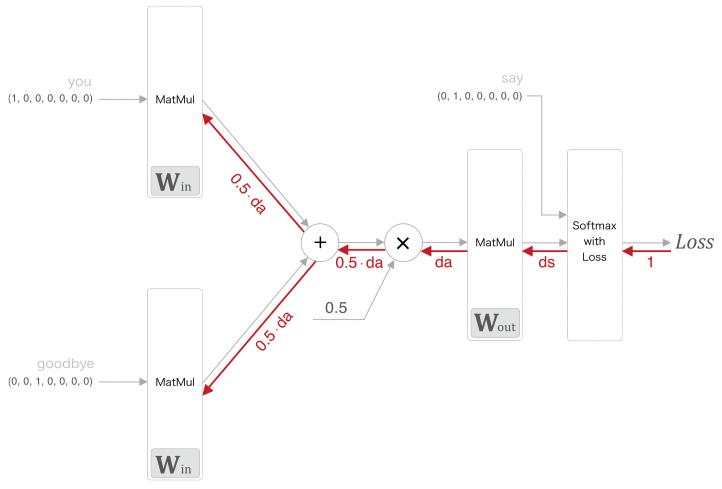
# coding: utf-8
import sys
sys.path.append('..') # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from common.trainer import Trainer
from common.optimizer import Adam
from simple_cbow import SimpleCBOW
from common.util import preprocess, create_contexts_target, convert_one_hot
window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)
model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
word_vecs = model.word_vecs # (5x7) 행렬 반환 W_in
# 행렬의 각 행 벡터가 단어의 word2vec 값
for word_id, word in id_to_word.items():
print(word, word_vecs[word_id])
실제로 학습을 돌리면 아래와 같은 $W_{in}$ 이 나오고 각 단어의 인덱스를 기반으로 열벡터를 출력하였다.
you [-1.1749326 1.2120602 -1.1711328 -1.1683513 -1.1166059]
say [ 1.2309499 -0.367042 1.238516 1.221913 1.1602981]
goodbye [-0.6956941 0.8612482 -0.721387 -0.7143741 -0.81281894]
and [ 0.91304606 -1.9012996 0.89655274 0.9373583 1.0937577 ]
i [-0.6829765 0.8541114 -0.7034645 -0.7197526 -0.8117175]
hello [-1.161014 1.2259955 -1.1638184 -1.1606017 -1.1285164]
. [1.182878 1.8289633 1.2051629 1.1582808 0.88485396]
CBOW 손실함수
Softmax 계층에서 Cross Entropy Error 를 이용해 loss 값을 계산하여 역전파 과정을 통해 $W_{in}$ 에서 단어의 word2vec 를 추출하는데
이는 사실 확률표기법을 코드로 모델화 한것일 뿐이다, 통계표기법으로 CBOW 의 손실함수를 수식화 하여 정의해보자.
말뭉치를 단어 시퀀스 $w_n$ 으로 표기하고 위와 같이 형성되어 있을 떄
| $w_t$ 가 출현될 확률은 $P(w_t | w_{t−1} ,w_{t+1})$ 이라 할 수 있다. $w_{t−1} ,w_{t+1}$ 이 주어졌을 때 $w_t$ 가 일어난 확률을 뜻한다. |
전체 말뭉치에 대해 음의 로그가능도를 사용하여 손실함수로 사용한다.
\[L = - \frac{1}{T}\sum^T_{t=1} \log P(w_t | w_{t−1} ,w_{t+1})\]통계표기법으로 보면 CBOW 학습의 목표는 위 손실함수값을 가능한 작게 만드는 것.
SkipGram
SkipGram 는 CBOW 에서 다루는 context 와 타깃을 역전시킨 모델이다.

한 단어로 부터 주변 단어(맥락)을 유추해 낸다.
모델의 형식은 아래와 같다.
$w_t$ 로부터 맥락 $w_{t-1}, w_{t+1}$ 이 출현될 확률은 $P(w_{t−1} ,w_{t+1} | w_t)$ 이며
이를 모델링한 방식이 SkipGram 모델이다.
맥락의 단어들 사이에 관련성이 없다고 가정(조건부 독립) 했을때 아래와 같이 변형 가능하다.
\[P(w_{t−1} ,w_{t+1} | w_t) = P(w_{t−1}| w_t) + P(w_{t+1}| w_t)\]CBOW 와 같이 전체 말뭉치에 대해 음의 로그가능도를 사용해서 손실함수로 사용한다.
단어분산표현 정밀도면에서 SkipGram 모델이 CBOW 보다 더 우수하지만 학습 속도는 느리다.
NNLM(Neural Net Lagnage model)
CBOW, SkipGram 모두 주변단어를 입력값으로 뉴럴넷에 접목시켰듯이
예측할 앞단어 n-gram 개수의 단어를 입력값으로 사용하여 뉴럴넷 구현한 방식이 NNLM
n-gram 문제를 뉴럴넷에 접목시킨것이 NNLM 모델이다.
NNLM 은 n-gram 개수의 과거 정보만을 참조함으로 앞으로 나올 내용을 파악할 수 없음으로,
단어의 함축(long-term)적인 값을 파악할 수 없다.
SGNS(Skipgram with Nagative Sampling)
기존 Word2Vec 을 위한 모델들은 출력값이 단어이고 벡터 값을 입력데이터, 출력데이터로 사용하다 보니 희소표현의 문제, 높은 연산량 처리문제가 있다.
위에서 설명한 SkipGram 모델 학습 효율역시 마찬가지로 좋지 않다.
여기에 Nagative Sampling 개념을 넣으면 학습효율을 높힐 수 있다.
SGNS 모델은 Word2Vec 학습 과정에서 관련이 높은 단어들에 집중하는 것이다.
예를들어 for, hard 두개의 주변관계인 단어를 입력값으로 넣으면 0 ~ 1 사이의 값이 출력되도록 하는 모델이다.
즉 두 단어를 입력하면 두 단어가 중심관계 혹은 주변관계인지 파악하는 모델이 SGNS 이다.
출력층의 개수가 1인 이진분류 문제이기 때문에 기존 Word2Vec 모델보단 학습 연산량이 적다.

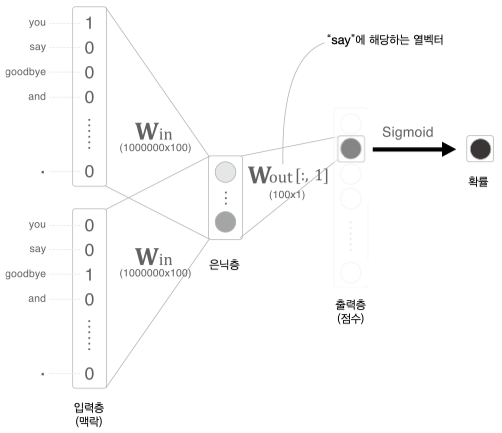
당연히 1에 가까우면 두 단어의 관계가 높다고 할 수 있다.
아래와 같이 [관계있는 단어, 관계없는 단어] 조합을 말뭉치에서 Sampling 하는데
관계없는 단어를 샘플링한다 하여 Nagative Sampling 이라 한다.
[studied, for] = 1
[hard, for] = 1
[the, for] = 1
[exam, for] = 1
[sky, for] = 0
[piano, for] = 0
Negative Sampling 하는 방법은 확률분포에 의존한다.
단어의 출현횟수를 기반으로 확률분포를 구하고 자주 등장하는 단어들을 샘플링 대상으로 삼는다.
이때문에 희소한 단어는 선택되기가 어렵다.
words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
np.random.choice(words, size=5, replace=False) # 중복x
# array(['say', 'you', 'goodbye', 'I', 'hello'], dtype='<U7')
p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
np.random.choice(words, p=p) # 확률분포 기반
# 'you'
가장 값이 높은 you 가 나올 확률이 높고 그다음으로 I 가 높음
낮은 분포도의 단어의 확률을 약간 높이기 위해 배열 p 를 구할 때 기존 확률분포에 임의의 실수 0.75 를 제곱하여 수행한다.
이렇게 구해진 단어들을 학습하는 과정은 아래 그림과 같다.
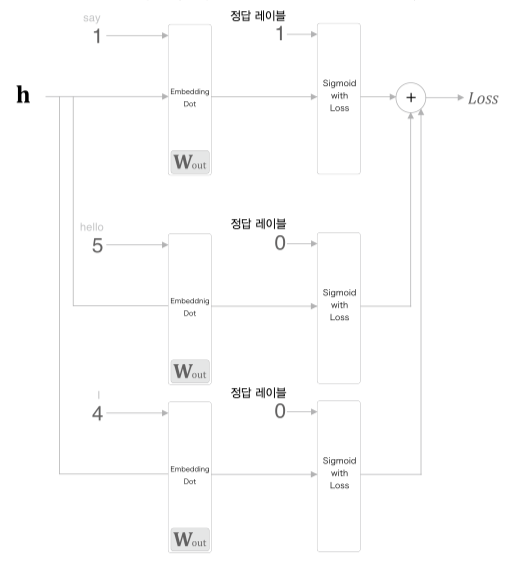
그림을 보면 학습시에 say 는 1, 그외의 hello 와 I 는 0 으로 처리하고
Cross Entropy Loss 함수를 사용하여 Loss 를 구한다.
단어 리스트에 대한 확률분포를 생성하는 클래스 UnigramSampler 를 살펴보자.
class UnigramSampler:
"""
corpus: 단어 id 리스트
power: 확률분포 제곱값
sample_size: 샘플링 수행 횟수
"""
def __init__(self, corpus, power, sample_size):
self.sample_size = sample_size
self.vocab_size = None
self.word_p = None
# 확률분포 p 구하는 과정
counts = collections.Counter()
for word_id in corpus:
counts[word_id] += 1
vocab_size = len(counts)
self.vocab_size = vocab_size
self.word_p = np.zeros(vocab_size)
for i in range(vocab_size):
self.word_p[i] = counts[i]
self.word_p = np.power(self.word_p, power)
self.word_p /= np.sum(self.word_p)
"""
target: 긍정적 샘플 단어 id 리스트
"""
def get_negative_sample(self, target):
batch_size = target.shape[0]
negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)
for i in range(batch_size):
p = self.word_p.copy()
target_idx = target[i]
p[target_idx] = 0
p /= p.sum()
# p 로부터 sample_size 만큼
negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)
return negative_sample
# You say hello and I say hello. 의 word id
corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample) # [[0 3]
class NegativeSamplingLoss:
"""
W: 가중치
corpus: 말뭉치 id 리스트
power: 확률분포 제곱
sample_size: 부정 샘플링 횟수
"""
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads = [], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
def forward(self, h, target):
batch_size = target.shape[0]
negative_sample = self.sampler.get_negative_sample(target)
# 긍정적 예 순전파
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# 부정적 예 순전파
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample_size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label)
return loss
def backward(self, dout=1):
dh = 0
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = l0.backward(dout)
dh += l1.backward(dscore)
return dh
최적화 - Embedding
embedding: 끼워넣다
만약 말뭉치에서 단어의 개수가 1000000개 단위, 은닉층의 뉴런개수가 100개일 경우 $W_{in}$ 은 1000000x100 크기의 행렬을 계산해야 한다.
(출력 층도 마찬가지로 100x1000000)
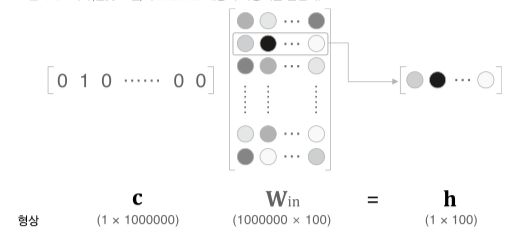
사실 원핫백터과 가중치 $W_{in}$ 은 서로 행렬곱을 할 필요가 없다.
단어가 해당되는 원핫백터 index 외에는 모두 0이기 때문에 index 에 해당하는 $W_{in}$ 의 행백터만 추출해서 다음 계층으로 넘기면 된다.
이 추출계층을 Ebmedding 계층이라 한다.
순전파는 가중치 $W$ 의 특정 행백터만 추출만 하면 되고
역전파는 앞단에서 전달받은 기울기를 다음층으로 그대로 흘려보내면 된다.(index 에 맞게)
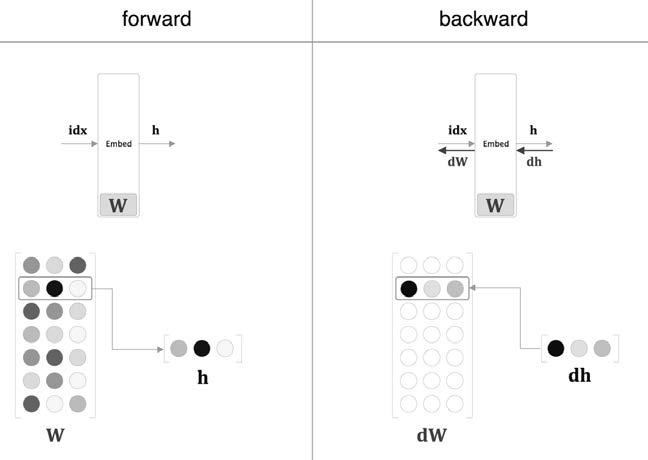
단 해당 단어의 index 를 제외한 $dW$ 의 모든 행백터는 0으로 초기화 한다.
인스턴스 변수 idx 에는 단어ID(추출행)을 배열로 저장한다.
window size 만큼의 원핫백터를 통해 가중치를 구하다 보니 동일한 단어가 포함될 수 있다.
아래와 같이 단어 index 가 여러번 포함될 경우
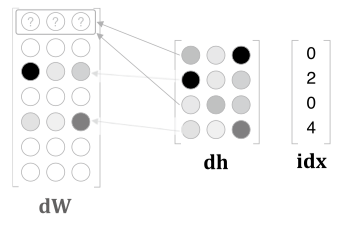
할당이 아닌 더하기를 사용해 $dW$ 를 구성한다.
class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx
out = W[idx]
return out
def backward(self, dout):
dW, = self.grads
dW[...] = 0
np.add.at(dW, self.idx, dout)
return None
GloVe
GloVe(global vectors for word representation)
직역하면 단어 표현을 위한 전역 벡터
Co-occurrence matrix(동시출현 행렬) 아이디어를 사용한 단어 통계방식을 사용한다.
만약 아래 3가지 문장있을 때, 해당 문장의 모든 단어의 연관관계를 하나의 matrix 로 표현할 수 있다.
I enjoy flying
I like NLP
I like deep learning
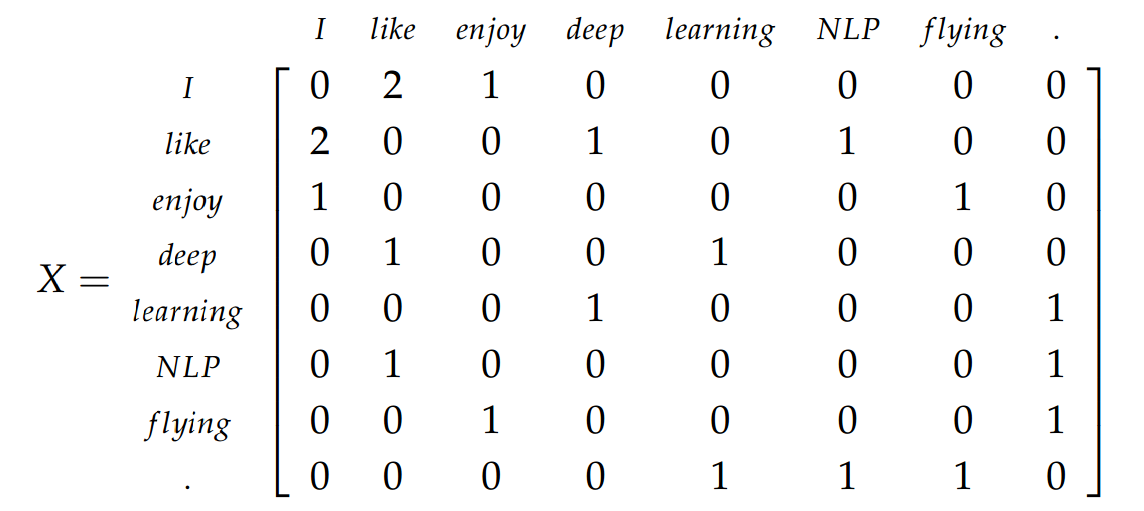
해당 단어가 바로 옆에 단어를 카운팅하여 Co-occurrence matrix 행렬로 표현할 수 있다.
그리고 단어 $i$ 이후 단어 $k$ 가 나올 확률은 아래와 같이 구할 수 있다.
\[P(k|i) = \frac{X_{i,k}}{\sum_j X_{i,j}} = \frac{X_{i,k}}{X_i}\]손실함수
GloVe 의 손실함수는 아래와 같다.
단어 $i, k$ 의 임베딩 벡터를 $w_i, w_k$ 로 표현,
그리고 단어 $i$ 의 주변단어의 임베팅 벡터를 $\hat{w_j}$ 로 표현할 때
| 두 단어 $w_i, w_k$ 의 내적값을 $p(k | i)$ 로 만드는 것이다. |
보통 뉴럴넷에서 쉽게 연산하기 위해 로그확률을 사용한다.
이런 아이디어가 나올 수 있었던 과정은 아래와 같다.
주변 단어벡터 $\hat{w_k}$ 가 있을 때 현재단어를 추측하기 위한 후보단어벡터를 $w_i, w_j$ 로 가정
\[f(w_i, w_j, \hat{w_k}) = \frac{P(i|k)}{P(j|k)}\]$f$ 값이 클수록 단어 $i$ 출현확률이 높은것이고
$f$ 값이 작을수록 단어 $j$ 출현확률이 높은것이다.
3개의 벡터를 입력값으로 넣어 하나의 스칼라값으로 출력하기 위해 모델을 아래와 같이 변경
\[f((w_i - w_j)^T, \hat{w_k}) = \frac{P(i|k)}{P(j|k)}\]두 백터 $(w_i - w_j)^T, \hat{w_k}$ 를 내적시킬 예정이다.
함수의 준동형성 성질을 이용해 아래와 같이 변경
\[\begin{aligned} &f((w_i - w_j)^T \cdot \hat{w_k}) \\ &= \frac{f(w_i^T \cdot \hat{w_k})}{f(w_j^T \cdot \hat{w_k})} \\ &= \frac{P(i|k)}{P(j|k)} \end{aligned}\]여기에 $f$ 를 지수함수 $\exp$ 로 사용한다 가정하면
\[\frac{\exp(w_i^T \cdot \hat{w_k})}{\exp(w_j^T \cdot \hat{w_k})} = \frac{P(i|k)}{P(j|k)}\]결국 맨 처음 알아봤던 아래식으로 변경 가능하다.
\[w_i^T \cdot \hat{w_k} = \log P(k|i)\]손실함수를 계산하기 위해 수식을 풀어보면 아래와 같다.
\[w_i^T \cdot \hat{w_k} = \log P(k|i) = \log(\frac{X_{i,k}}{X_i}) \\ = \log X_{i,k} - \log X_i\]여기서 $i$ 와 $k$ 의 위치를 교환하면 아래와 같은데
\[w_k^T \cdot \hat{w_i} = \log X_{k,i} - \log X_{i,k} - \log X_k\]둘다 같은 벡터에 대한 내적이지만 두 값이 서로 일치하지 않는, 교환법칙이 성립하지 않는 문제가 발생했다.
그래서 $\log X_i, \log X_k$ 값을 없애기 위해 bias 값을 사용하여 없에도록 가정한다.
\[w_i^T \cdot \hat{w_k} + b_i + \hat{b_k}= \log X_{i,k}\]그래서 손심할수는 아래와 같이 정의할 수 있다.
\[Loss = (w_i^T \cdot \hat{w_k} + b_i + \hat{b_k} - \log X_{i,k}) ^ 2\]추가 고려사항
로그확률 특성상 $\log 0$ 이 무한대 음수꼴임으로 아래와 같이 1을 더하줘야함
\[\log (1 + X_{i,k})\]단어개수는 많은데 문장개수가 충분하지 않은, 말뭉치가 충분하지 않을경우
Co-occurrence matrix 의 대부분값이 0인 희소표현 문제가 발생함
FastText
학습데이터도 단어를 사용하는 것이 아닌, 단어의 문자 기준 n-gram 으로 토큰화 하여 학습데이터로 사용한다.
n-gram 을 3으로 설정해서 mouse 단어를 나눌경우 아래와 같다.
mouse -> [mo, mou, ous, use, se]
FastText 는 Facebook 에서 개발한 Word2Vec 알고리즘으로
단어를 더 쪼갠 subword 개념을 사용하는 모델이다.
학습데이터가 늘어나 더 많은 리소스를 필요로하겠지만 이런 아이디어를 도입하면서 아래와 같은 문제들을 해결할 수 있다.
1. OOV(Out of Vocabulary)
학습용 corpus 에 존재하지 않아 모르는 단어에 대해 어느정도 단어를 벡터값으로 처리 할 수 있다.
어간(Stem), 접사(Affic)를 분리하는 어간추출 방식을 사용하는 것도 이 OOV 문제를 해결하기 위한것이라 할 수 있다.
2. Rare Words
FastText 는 Rare Word 문제 에 대해서도 강하다.
빈도수가 적은 단어들은 정제, 추출 과정에서 제외되거나,
학습한다 하더라도 충분한 학습도 되지 않기에 결과가 좋지않다.
3. Typo Error
입력된 단어의 오타 문제에 대해서도 강하다,
어떻게 보면 오타 단어도 Rare Words 라 생각할 수 있음으로.
사전훈련모델
충분한 데이터셋이 존재하지 않을경우 underfitting 문제가 발생하는데
이를 해결하기 위해 pretrain 되어있는 모델을 가져와 사용한다.
CBOW, GloVe, FastText 등으로 훈련된 사전모델들이 존재한다.
보통 차원은 512 를 많이 쓰고 사전에 학습된 Pretrained Embeddings 이 있음