자연어 처리(Natural Language Processing)

말은 단어의 나열, 구성이다.
즉 단어는 의미의 최소단위라 할 수 있다.

프로그래밍 언어는 기계적이고 일련의 규칙이 있는 기계적인 측면에
영어, 한국어와 같은 자연어는 규칙이 완화된 부드러운 언어라고 할 수 있다.

컴퓨터에게 단어의 의미를 이해시키는 것이 자연어 처리의 첫 발이다.

전처리

컴푸터에 바로 자연어를 입력시키지 않고 정제도니 데이터를 통해 자연어처리를 진행한다.
아래와 같은 몇가지 단계를 거치게 한다.

tokenization(토큰화)
cleaning, stemming(정제 및 추출)
encoding(인코딩)

[토큰화, 정제 및 추출 과정] 은 한번으로 끝나지 않고 계속 반복시킬 수 있다.

학습데이터, 혹은 분석데이터로 입력받은 말뭉치를 바로 사용하지 않고
항상 전처리 작업을 통해 정제된 데이터로 변환해야 한다.

토큰화(tokenization)

영문장의 경우 [공백, 계행, 컴마, 따옴표] 등을 기준으로 토큰화해주면 된다.
유명화 표준 토큰화 기준으로 Treebank Tokenization 가 있다.

from nltk.tokenize import TreebankWordTokenizer
s = "hi, my name can't hello,"
TreebankWordTokenizer().tokenize(s)
# ['hi', ',', 'my', 'name', 'ca', "n't", 'hello', ',']

정제(cleaning)

아래와 같은 과정을 데이터를 없애는, 정제과정이라 할 수 있다.

대소문자 구분 제거
등장빈도가 적은 단어 제거(Removing Rare words)
길이가 잛은 단어 제거(Removing words with a very short length)
불용어 제거(Stopword)

대세에 영향을 끼치지 않는, 자주 사용되지 않는 단어의 경우 정제(cleaning) 해야한다.

길이가 짧은 단어의 경우 대부분 불용어에 해당한다.
[it, at, to, on, in, by] 등

불용어의 경우 아래와 같은 문맥에 큰 영향을 끼치지 않는 단어를 뜻한다.
[I, my, me, over, a, an, 관사, 조사, 접미사] 등

정제과정을 조건없이 처리할 경우 US(unite state) 를 us(우리) 로 인식되는 기현상이 발생할 수 있다.

이런 이유로 정체 및 추출은 아직은 기계가 인식하긴 어려운 단계로 사람이 어느정도 rule 을 정해줄 필요가 있다.

추출(stemming)

추출은 여러방식이 있지만 가장 대표적인건 어간(Stem)과 접사(Affic)를 분리 어간추출이다.

단어의 어간이라 할 수 있는 부분에서 [형용사, 명사]화 시키는 접사 부분을 지워버리는 과정이다.

fomalize → formal
kindness → kind
electrical → electric

물론 해당 명사가 킬링워드일 경우는 어간추출을 하면 안되지만
단순 스팸메일 구분이라던지 등의 작업에선 굳이 접사를 유지시킬 필요는 없다.

어간추출을 위한 대표적인 알고리즘으로 Porter Stemming 알고리즘 이 있다.

표제어추출(Lemmatization)

Lemmatization 은 원형 복원 이라는 뜻이기도 하다.
사전에 기반한 단어의 표준화를 진행한다.

is, are → be
playing → play

인코딩

실제 컴퓨터가 단어의 뜻을 이해하진 않는다.
인코딩 이라는 단어를 숫자로 변경하는 과정을 거쳐야한다.

단어의 의미를 숫자로 파악할 수 있게 해주는 인코딩 기법은 대표적으로 아래 3가지가 있다.

시소러스기반 기법
통계기반 기법
추론기반 기법

시소러스(thesaurus)

시소러스는 단어를 의미에 따라 분류·배열한 일종의 유의어(類義語) 사전, 단어 네트워크이다.

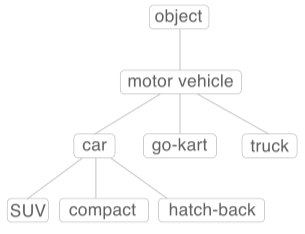
아래와 같이 단어 네트워크를 구성해두고 사용하면 된다.

car = auth, automobile, machine, motocar

위처럼 유의어들간의 그룹 관계을 짖거나 단어간의 상위/하위 관계를 하나의 집합으로 만들면
단어 사이의 연결을 정의, 단어 네트워크 생성할 수 있다.

단어 네트워크가 있으면 어느정도 컴퓨터에게 단어의 의미를 이해킬 수 있다.
하지만 단어의 모음집을 사람이 직접 구축해야 하기 때문에 여러 단점이 있어 최근 딥러닝이 나온 시점부터는 잘 사용하지 않는다.

시대 변화에 대응하기 어렵다.
큰 인적 비용
단어간의 미묘한 차리 (부정 긍정 등)

WordNet: 프리스턴 대학교에서 1985 년부터 구축하기 시작한 전통 있는 시소러스, 지금까지도 많은 자연어 처리 분야에서 사용되고 있다.

통계기반 기법

아래는 text 문자열을 통계기반 기법으로 표현하기 위해 인코딩 하는 과정이다.

단순 단어 출현 순서에 의한 index 를 인코딩값으로 사용한다.

아래 예제에산 예시를 위해 간단히 단어-index map 을 corpus 로 사용한다.

import numpy as np

text = 'You say goodbye and I say hello.'
text = text.lower()
text = text.replace('.', ' .')
print(text)
# 'you say goodbye and i say hello .'
words = text.split(' ')
print(words)
# ['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']
word_to_id = {}
id_to_word = {}
for word in words:
    if word not in word_to_id:
        new_id = len(word_to_id)
        word_to_id[word] = new_id
        id_to_word[new_id] = word

print(id_to_word)
# {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6:'.'}
print(word_to_id)
# {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}

corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
print(corpus)
# [0 1 2 3 4 1 5 6]

corpus(말뭉치): 자연어 처리 연구나 애플리케이션을 염두에 두고 수집된 텍스트 데이터
단순 단어의 집합이 아닌 사람의 지식을 담겨져 있는 단어의 나열이다.

통계 기반 기법에선 corpus 를 사용한다.
구글 뉴스, 위키백과, 유명 소설 등을 말뭉치 데이터로 사용할 수 있다.

PTB(Penn Treebank) 데이터 셋
벤치마크 측정시에 자주 사용되는 말뭉치 데이터 셋, 토마스 미콜로프의 웹페이지에서 다운 가능하다
https://raw.githubusercontent.com/tomsercu/lstm/master/data/ptb.train.txt
https://raw.githubusercontent.com/tomsercu/lstm/master/data/ptb.test.txt
https://raw.githubusercontent.com/tomsercu/lstm/master/data/ptb.valid.txt

TF-IDF

Term Frequency - Inverse Document Frequence

단어가 얼마나 중요한지를 수치적으로 나타낸 가중치값이다.

\[TF-IDF = tf(d,t) \times idf(d,t)\] \[idf(d, t) = \log\frac{N}{df(t)}\]

$tf(d,t)$: 특정 문서 $d$ 에서 특정단어 $t$ 의 등장횟수
$df(t)$: 특정 단어 $t$ 가 등장한 문서개수
$N$: 총 문서개수

Markov Chain

이미 $n-1$ 개의 단어가 주어진 상황에서 다음에 등장할 단어의 확률을 아래 수식처럼 표현할 수 있다.

\[P(w_n | w_1, w_2, \cdots, w_{n-1}) = \frac{P(w_1, \cdots, w_n)}{P(w_1, \cdots, w_{n-1})}\]

$w_1 \rarr w_n$ 까지 모두 일치할 확률의 표본을 구하는것은 거의 0 에 수렴한다.
sparsity problem(장기의존성 문제, 희소성 문제) 이라 부른다.

또한 $w_1$ 이 $w_3, w_4$ 가 출력되는데 영향을 끼칠 수 도 있기 때문에 단편적으로만 확률을 구해선 안된다.

sparsity problem을 해결하기위해 n-gram 문제를 사용할 수 있다.
만약 n-gram 값을 2로 설정하면 아래 확률값을 구하기만 하면 된다.

\[p(w_n | w_{n-2}, w_{n-1})\]

물론 n-gram 값이 작을수록 정확성을 떨어지는 모델이 된다.

한글의 경우 단어순서가 달라도 상관없기 때문에 Markov chain 모델은 한글에서 사용하긴 힘들다.

분산 표현, 분포 가설

모든 색들은 하나의 벡터값(RGB) 으로 표현할 수 있다.

단어또한 백터로 표현할 수 있는데 이를 분산 표현(distributional representation) 이라 한다.

단어를 벡터로 표현하기 위한 가장 중요한 아이디어는 단어의 의미가 주변 단어에 의해 형성된다는 것
이를 분포 가설(distributional hypothesis) 이라 한다.

단어를 벡터로 표현하는 대부분의 연구가 분포 가설에 기초한다.

즉 단어 자체에는 의미가 없고, 그 단어가 사용 된 context(맥락) 가 의미를 형성한다는 것

예로 I drink beer I guzzle beer 두 문장에서 drink, guzzle 단어 앞에는 I, 뒤에는 beer가 출력된것으로 보아
[drink, guzlle] 두 단어가 매우 가까운 의미인 것을 알 수 있다.

즉 주변의 다른 단어(context) 가 단어에 대한 백터를 구하는 키값으로 사용될 수 있다.
context 는 좌우의 각 N개 단어를 뜻하며 단어마다 맥락의 크기는 다를 수 있고 이 크기를 window size 라 한다.

예를 들어보자.

you say goodbye and i say hello.

위 문장에서 window size 를 1로 설정했을 때 각 단어의 맥락에 포함되는 빈도수를 차트로 표시하면 아래와 같다.

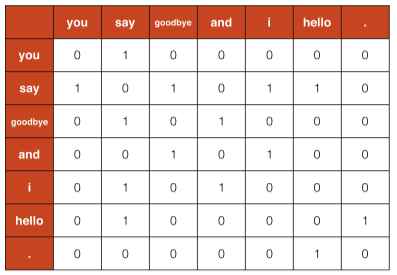
코드로 표현하면 아래와 같다.

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''동시발생 행렬 생성

    :param corpus: 말뭉치(단어 ID 목록)
    :param vocab_size: 어휘 수
    :param window_size: 윈도우 크기(윈도우 크기가 1이면 타깃 단어 좌우 한 단어씩이 맥락에 포함)
    :return: context 행렬
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

text = "you say goodbye and i say hello."
corpus, word_to_id, id_to_word = preprocess(text)
vacap_size = len(word_to_id)
C = create_co_matrix(corpus, vacap_size)
print(C)
# [[0 1 0 0 0 0 0]
#  [1 0 1 0 1 1 0]
#  [0 1 0 1 0 0 0]
#  [0 0 1 0 1 0 0]
#  [0 1 0 1 0 0 0]
#  [0 1 0 0 0 0 1]
#  [0 0 0 0 0 1 0]]

출력된 Corpus matrix 가 각 단어의 백터 로 사용되게 된다.

단어간 유사도

백터간의 유사도는 내적이나 유클리드 거리를 사용해도 되지만
단어벡터의 유사도는 대표적으로 코사인 유사도(cosine similarity) 를 사용한다.

cosine similarity

\[\mathrm{similarity}(x, y) = \frac{x \cdot y}{||x|| \cdot ||y||} = \frac{x_1y_1 + ... + x_ny_n}{\sqrt{x_1^2+...+x_n^2} \sqrt{y_1^2+...+y_n^2}}\]

즉 자신과 비슷한 형태의 단어 배열을 가지고 있는 단어에게 높은 similarity 값이 출력되게 된다.
코사인 유사도는 -1 ~ 1 사이의 값으로 출력된다.

코드로 구현하면 아래와 같다

def cos_similarity(x, y, eps=1e-8):
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

모든 값이 0 일경우 divide by zero 에러가 발생함으로 작은 실수값 1e-8 (0.00000001) 을 분모에 더해준다.

you 단어를 선택해서 다른 단어들에 대해 유사도를 검색해보자.

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    if query not in word_to_id:
        print('%s(을)를 찾을 수 없습니다.' % query)
        return

    print('\n[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    # 코사인 유사도 계산
    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    # 코사인 유사도를 기준으로 내림차순으로 출력
    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return

most_similar('you', word_to_id, id_to_word, C, top=5)
# [query] you
#  goodbye: 0.7071067691154799
#  i: 0.7071067691154799
#  hello: 0.7071067691154799
#  say: 0.0
#  and: 0.0

이전에 구했던 단어백터 와 단어 인덱스를 전달하면 위와 같이 출력된다.

i 의 유사도가 높게 출력되는 것은 이해 되지만 goodbye, hello 의 유사도가 상당히 높게 나왔는데,
이는 말뭉치가 너무 작기 때문이다.

Levenshtein Distance

편집 거리(Edit Distance) 라고도 불리는 알고리즘

특정 단어에서 몇번 삽입(Insertion), 삭제(Deletion), 대체(Replacement) 해야 목표 단어로 변화되는지 구하는 방법이다.

이 연산과정에서 몇번 을 Levenshtein Distance 라 하며 작을수록 두 단어가 비슷하다 할 수 있다.

동일: 대각선 수
변경: 대각선 수 + 1
삽입: 상단수 + 1
삭제: 좌측수 + 1

아래 그림은 [delete, delegate] 두 단어의 편집거리를 구하는 그림

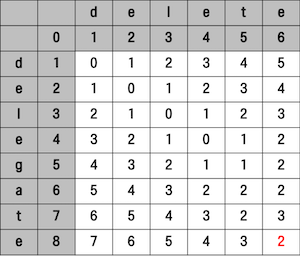
Jaccard Distance

단어 A, B 를 문자배열로 만들어
아래 식을 사용해 각 단어 리스트의 집한 연산을 통해 거리를 구할 수 있다.

\[J(A,B) = \frac{|A \cap B|}{|A \cup B|}\]

PMI (Pointwise Mutual Information: 점별 상호 정보량)

위에서 분포 가설에 의해 구한 단어 백터는 단어의 동시발생 벡터 이라 할 수 있고 두 단어의 연관성을 뜻하게 된다.

예로 the car 처럼 자주 출현되는 [the, car] 고빈도 두 단어는 크게 연관은 없지만
위와 같은 방식으로만 유사성을 구할경우 강한 관련성을 가지게 된다.

car 는 drive 와 같은 단어와 더 높은 관련성을 가져야 겠지만
단순 빈도수로 인해 the 가 더 높은 관련성을 가는다는 것.

이런 이유로 단순 동시발생 백터를 사용하지 않고 PMI 라는 단어 벡터를 사용한다.

두 단어 $x, y$ 의 PMI 를 구하는 새로운 방법은 아래와 같다.

\[\mathrm{PMI}(x,y) = \log_2\frac{P(x,y)}{P(x)P(y)}\]

전체 단어량에서 등장하는 단어의 빈도수를 분모에 넣어 해당 단어의 중요도를 하락시킨다.

추가로 두 단어의 동시 발생횟수가 0 일 경우 $P(x,y) = 0$ 이 될경우
$\log_2 0 = -\infin$ 임으로 PMI 지수를 0 으로 치환한다.

\[\mathrm{PPMI}(x,y) = \max(0, \mathrm{PMI}(x, y))\]

Positive PMI 라 함

코드로 각 단어벡터에 PPMI 연산 방법을 정의

def ppmi(C, verbose=False, eps = 1e-8):
    '''PPMI(점별 상호정보량) 생성

    :param C: 동시발생 행렬
    :param verbose: 진행 상황을 출력할지 여부
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% 완료' % (100*cnt/total))
    return M

C = create_co_matrix(corpus, vacap_size)
PPMI = ppmi(C)
print(C)
# [[0 1 0 0 0 0 0]
#  [1 0 1 0 1 1 0]
#  [0 1 0 1 0 0 0]
#  [0 0 1 0 1 0 0]
#  [0 1 0 1 0 0 0]
#  [0 1 0 0 0 0 1]
#  [0 0 0 0 0 1 0]]
print(PPMI)
# [[0.        1.8073549 0.        0.        0.        0.        0.       ]
#  [1.8073549 0.        0.8073549 0.        0.8073549 0.8073549 0.       ]
#  [0.        0.8073549 0.        1.8073549 0.        0.        0.       ]
#  [0.        0.        1.8073549 0.        1.8073549 0.        0.       ]
#  [0.        0.8073549 0.        1.8073549 0.        0.        0.       ]
#  [0.        0.8073549 0.        0.        0.        0.        2.807355 ]
#  [0.        0.        0.        0.        0.        2.807355  0.       ]]

기존의 단어간의 동시발생 단어 벡터 와 PPMI 단어 벡터를 비교

하지만 이런식의 단어벡터 연산은 큰 문제가 있는데
단어의 수가 늘어날 수록 벡터의 차원수가 늘어난다는 것.

단순 7 단어 문장에 사용된 행렬 요소개수를 확인해보면 $7^2$ 로 늘어남을 알 수 있음

SVD(Sigular Value Decomposition: 특이값 분해)

말뭉치 안에 단어 중복되지 않은 단어 10000개가 존재할 경우 벡터의 개수가 10000 개가 되고 이를 연산하는 것은 현실적이지 못하다.
이때문에 벡터의 차원수를 감소시키는 차원감소 기법중 하나인 특이값 분해(SVD: Sigular Value Decomposition) 를 사용한다.

https://angeloyeo.github.io/2019/08/01/SVD.html https://darkpgmr.tistory.com/106

임의의 행렬 $X$ 에 대하여 아래 수식과 같이 3가지 행렬 $U, S, V$ 의 곱으로 분해한다는 뜻.

\[X = USV^T \\ A = U \Sigma V^T\]

문서에 따라 일부 기호를 다르게 표현한다.

$X$: $m \times n$ 임의의 행렬
$U$: $m \times m$ 직교행렬
$S$: $m \times n$ 대각행렬
$V$: $n \times n$ 직교행렬

기하학적으로 아래와 같다.

다시말해 행렬 $X$ 는 $V^T$ 로 회전, $S(\Sigma)$ 으로 스케일 변환, $U$ 로 다시 회전하는 선형변환을 위한 행렬 이다.

직교행렬 (Orthogonal Matrix) https://www.youtube.com/watch?v=lICAZ9Vqlq4 아래 조건을 만족하는 행렬.
$A A^T = A^T A = I $ 선형대수학에서 직교행렬(Orthogonal Matrix)은 행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이루는 실수 행렬이다.

$S(\Sigma)$ 는 $m$ 과 $n$ 크기에 따라 아래와 같이 구성될 수 있다.

\[\begin{pmatrix} \sigma_1 & 0 & \cdots & 0 \\\\ 0 & \sigma_2 & \cdots & 0 \\\\ {} & {}& \ddots & {} \\\\ 0 & 0 & \cdots & \ \sigma_n \\\\ 0 & 0 & \cdots & \ 0 \\\\ \vdots & \vdots & \vdots & \vdots \\\\ 0 & 0 & \cdots & 0 \end{pmatrix} \begin{pmatrix} \sigma_1 & 0 & \cdots & 0 &0 & \cdots & 0 \\\\ 0 & \sigma_2 & \cdots & 0 & 0 & \cdots & 0\\\\ {} & {}& \ddots & {} & {} & {} & {}\\\\ 0 & 0 & \cdots & \ \sigma_m & 0 & \cdots & 0 \end{pmatrix}\]

이제 SVD 가 어떻게 차원축소를 하는지 알아보자.

예를들어 직교 하는 두 벡터 $\vec{x},\vec{y}$ 의 백터집합을 행렬 $V$ 로 표현하고 해당 벡터 집합을 행렬 $X$ 로 선형변환 했을때 백터 $\vec{A_x}, \vec{A_y}$ 가 출력된다고 해보자.

\[XV = \begin{bmatrix} \vec{A_x}, \vec{A_y} \end{bmatrix}\]

백터 $\vec{x},\vec{y}$ 와 변환된 백터 $\vec{A_x}, \vec{A_y}$ 의 크기는 다를것이고 그 차이룰 scaling factor 혹은 singular value(특이값) 이라 부른다.

특이값의 크기를 $\sigma_n$ 로 나타내며 행렬 $S(\Sigma)$ 표기하고 그리고 $\vec{A_x}, \vec{A_y}$ 를 크기 1로 정규화하여 백터 $\vec{u_x}, \vec{u_y}$ 로 표현하고 백터들의 집합을 행렬 $U$ 로 나타내었을 때
선형변환의 관점으로 아래처럼 구성할 수 있다.

\[XV = US\]

직교행렬의 특성을 사용하여 아래처럼 식을 정리 할 수 있다.

\[XVV^T = USV^T \\ X = USV^T \\ X = \sigma_1 \vec u_1 \vec v_1^T + \sigma_2 \vec u_2 \vec v_2^T +\cdots+ \sigma_m \vec u_m \vec v_m^T \ (m < n)\]

차원의 수를 줄이려면 아래 그림처럼 특이값 행렬의 크기를 조절하면 된다.

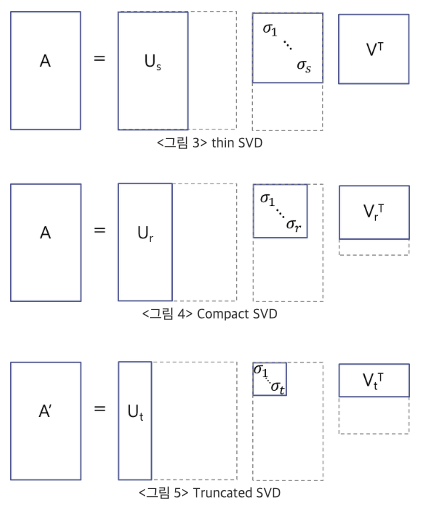
행렬 $X$ (그림에선 $A$) 를 일반적인 이미지로 구성하고 특이값 행렬의 크기를 줄여서 입력되는 이미지를 확인하면 아래와 같이 변화된다.

SVD 는 비단 이미지 행렬에서만 사용되는 것이 아니라
단어벡터나 행렬로 표현할 수 있는 데이터에 적용 가능하다.