Neural Network
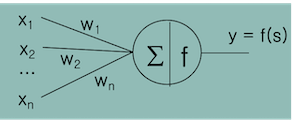
$x$: 입력값 $w$: 가중치
$ s = x_1w_1 + x_2w_2 + … + x_nw_n = \sum^n_{i=1} x_i w_i $
$s$ 의 값이 threshold(임계치) 보다 크면 1을 출력, 그렇지 않으면 출력하지 않는다.
이런 형태의 함수를
Step Function이라 함
입력의 가중 합 $\sum$ 을 First Function,
함수 $f$ 을 Second Function 이라 부른다.
Perceptron (인공네트워크)
초창기 Artificial Neuron(인공 뉴런) 은 아래와 같다.
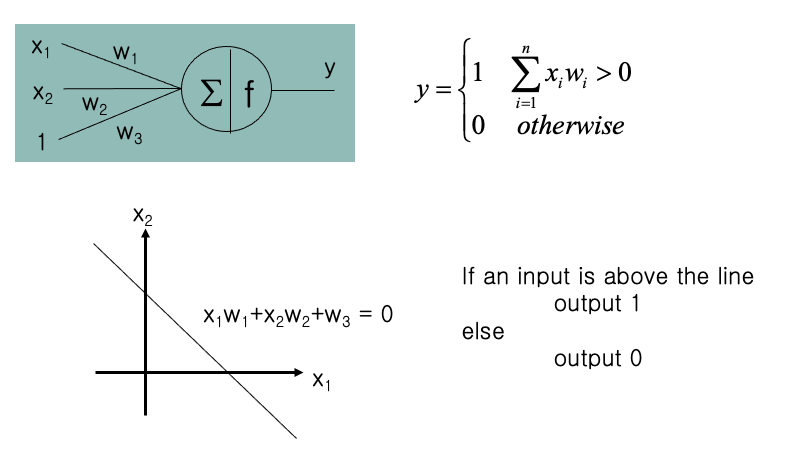
$w_3$ 를 threshold 로 사용
위처럼 직선의 방정식 $x_1w_1+x_2w_2+w_3 = 0$ 을 사용해 해당 linear 보다 위에있으면 1,
아니면 0을 반환하는 Second Function 정의한다.
뉴럴넷 을 구축하여 $o(\vec{w}, \vec{x})$ 를 구성하고 뉴럴넷 출력함수 $o$ 와 목표함수 $f$ 의 출력값이 같도록해야한다.
$o(\vec{w}, \vec{x}) = f(\vec{x})$
그러기 위한 가중치 $\vec{w} = (w_1, w_2, …, w_n)$ 을 찾는것이 뉴럴넷 의 목적이다.
다른말로 $\sum_{\vec{x}\in Data} [o(\vec{w}, \vec{x}) - f(\vec{x})]^2$ 값을 최소화 하는 것이다.
위 식을 Error Function, $E(\vec{w})$ 라 한다.
경사하강법
$E(\vec{w})$ 이 아래와 같은 그래프로 나타날 경우
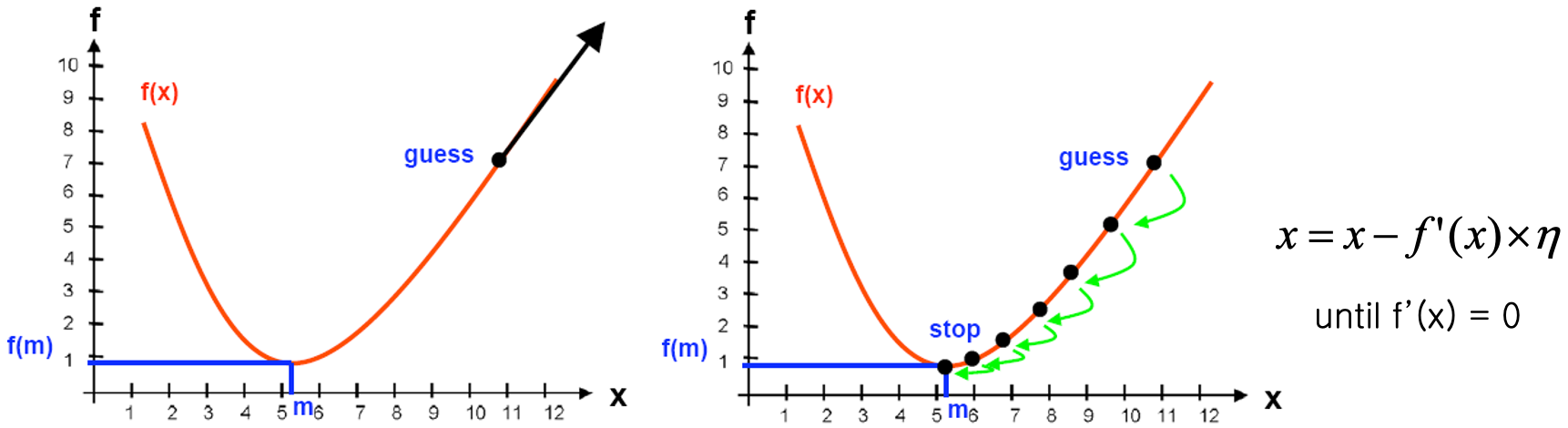
미분방정식을 풀 수있다면 변곡점, 기울기가 0 인 부분을 모두 구해서 가장 값이 작은 $f(m)$ 값을 구하면 된다.
미분방정식으로 표현할 수 없다면 $E(\vec{w})$ 을 최소화 하는 방법중 하나로 경사하강법이 있다. 위 그림 수식을 좀더 쉽게 설명하며 아래와 같다.
$x_{i+1} = x_i − \mathrm{step \ size \times Gradient} $
기울기의 반대방향으로 계속 $x$ 값을 이동시키기 때문에
$x$ 에 대한 출력값은 작아질 수 밖에 없다.
local minimum 으로 인해 경사하강법 하나만 사용하진 않지만 중요 Optimizer 중 하나이다.
위처럼 함수의 순간적인 기울기를 구해 사용자가 지정한 step size 인 $\eta$ 와 함께 연산,
최종적으로 기울기가 0이 되어 $x_{i+1}=x_i$ 값이 나오면 종료된다.
$\eta$ 가 너무 크면 이동량이 많아 발산하고 너무 작으면 많은 시간이 걸리게 되기에 적당한 step size 를 찾는것도 중요함.
시그모이드 미분
우리의 목적은 Error Function 을 최소화 하는 것이다.
$E(w)$ 의 미분을 하려면 $f(\vec{w})$ 에 대한 미분도 가능해야 하는데
최초의 Perception 에서는 Step Function 을 사용하기 때문에 미분이 불가능하다.
최근 Perception 에선 threshold 를 넘으면 바로 1로 변경되는 step function 을 사용하지 않고
완만한 곡선형태의 sigmoid 를 Second Function 으로 사용한다.
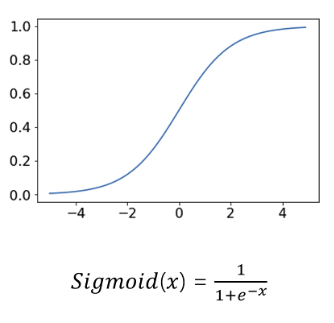
sigmoid 의 미분은 아래와 같다.
미분값이 결국 출력값과의 연산이기에 연산 리소스를 줄여주어 Error Function 을 찾기 쉽게 만들어준다.
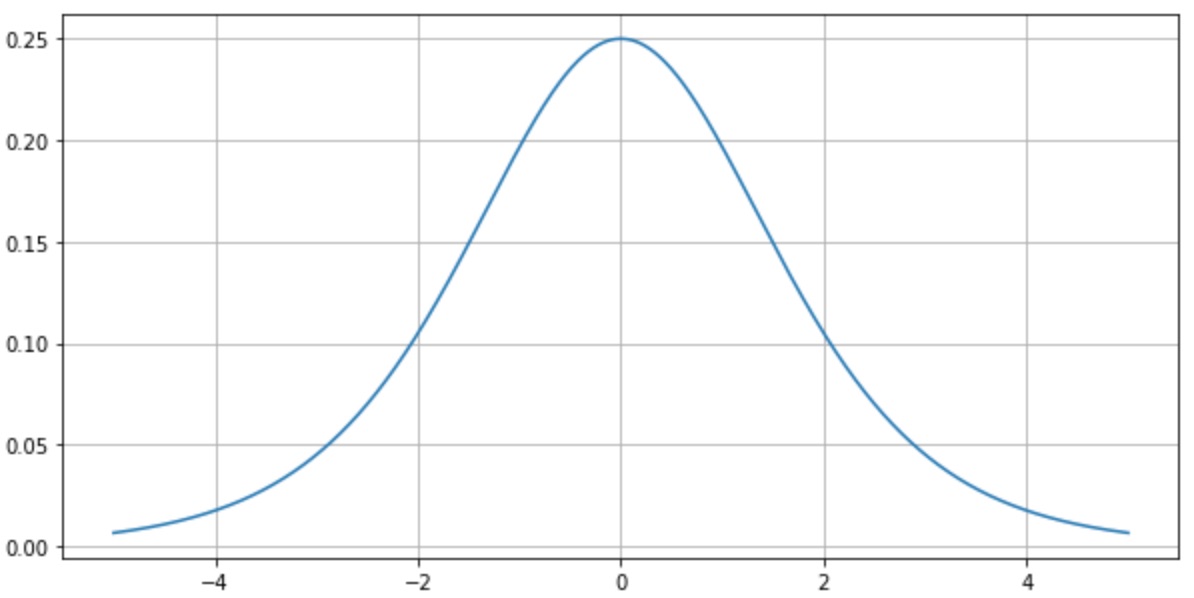
시그모이드 미분값의 최대값은 0.25 가 출력된다.
Forward Propagation (순방향 전파)
임의의 w 를 설정하여 아래와 같은 뉴럴넷 을 구성했을 때
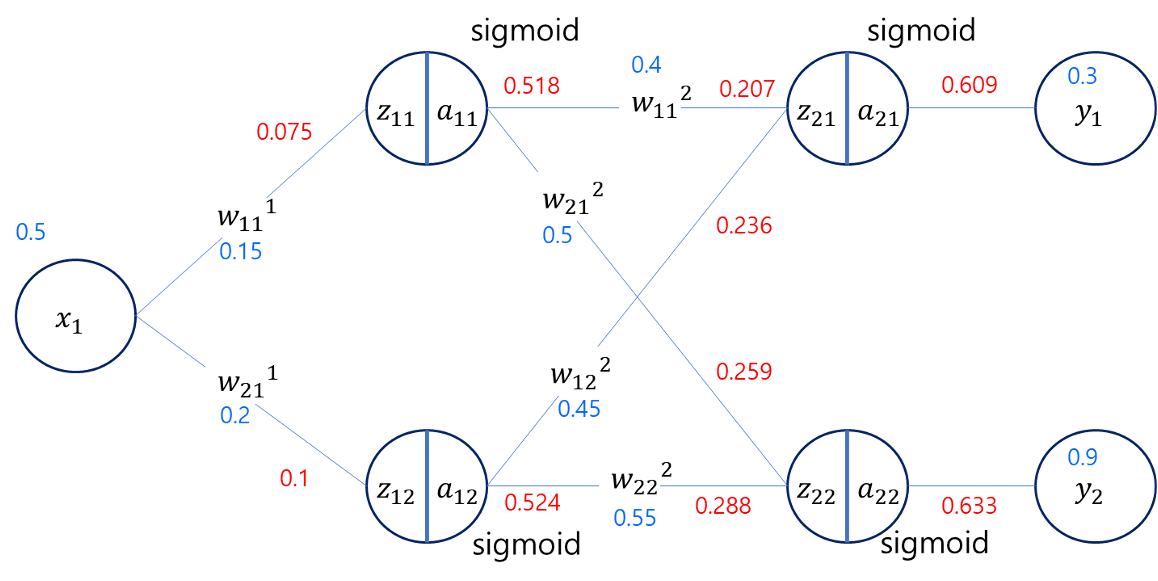 시작값 $x_1=0.5$ 로부터 최종 결과값 $y_1=0.3, y_2=0.9$ 을 예측했지만
각종 가중치와 시그모이드 함수를 통과한 결과는 $y_1=0.609, y_2=0.633$ 이다.
시작값 $x_1=0.5$ 로부터 최종 결과값 $y_1=0.3, y_2=0.9$ 을 예측했지만
각종 가중치와 시그모이드 함수를 통과한 결과는 $y_1=0.609, y_2=0.633$ 이다.
가중치 $w_n$을 조절하여 $y_1$의 값은 내리고, $y_2$의 값은 올려야 한다.
Back Propagation (역방향 전파)
가중치 조절은 역방향 전파의 미분으로 조절된다.
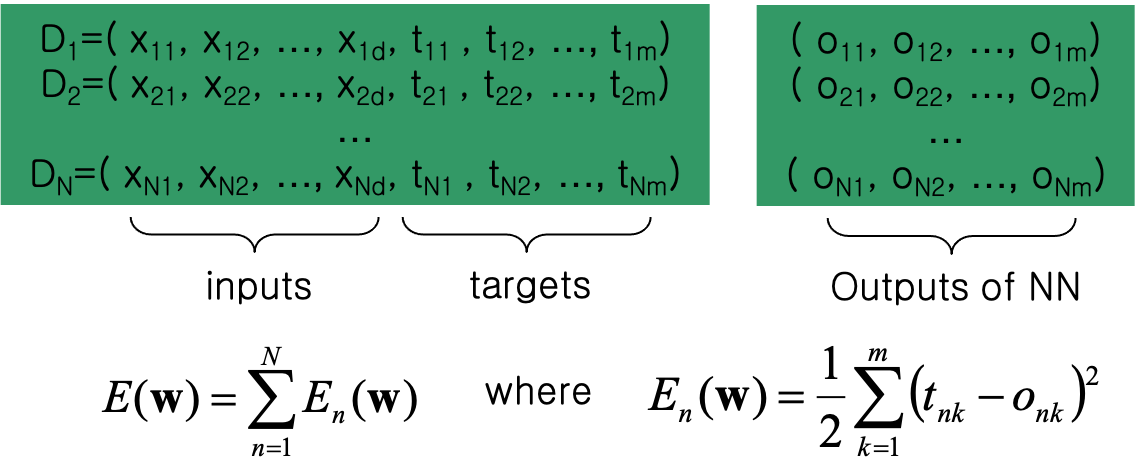
$D$ 는 트레이닝 데이터이다. 입력값이 $x_{11},…x_{1d}$ - $d$개 출력값이 $t_{11},…t_{1m}$ - $m$개
그림으로 그리면 아래와 같다.
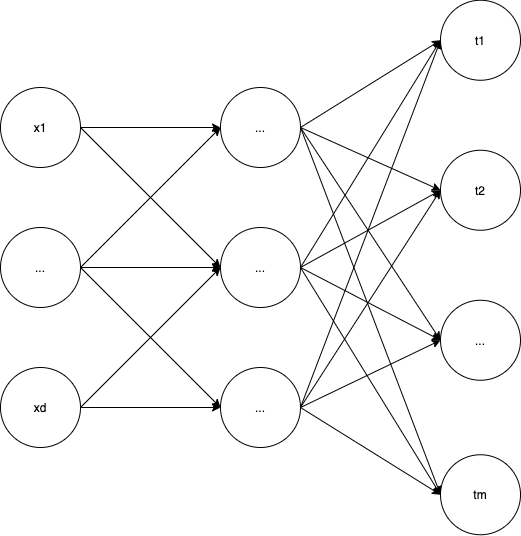
이러한 트레이닝 데이터가 $N$ 개 있다.
그리고 오차함수 각각의 $m$개의 $(t-o)$ 의 차이값에 제곱하여 $E(w)$ 를 구하고 더하고 이를 Error Function 으로 정의한다.
위 사진과 같은 상황일 때 실제 결과값 $t_{nk}$ 에 매칭되는 예측값 $o_{nk}$에 대한 Error Function 에 대입하면 아래와 같이 나온다.
위 Error Function 의 값을 $w_i$ 를 변경하면서 최소값을 찾아내는 것이 위에서 말한 뉴럴넷의 목적이다.
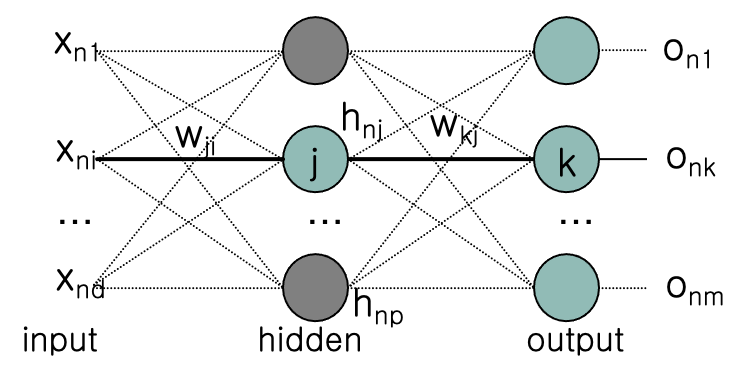
n 은 n 번째 데이터셋 의미로 생략해도 상관은 없다.
위 그림처럼 신경망의 깊이가 2개라면, 마지막 신경망($net_k$) 부분만 보았을때 모든 $h$ 값과 $o_{nk}$ 로 향하는 $w$ 값의 곱을 더하면 $o_ {nk}$ 가 나온다.
\[o_{nk} = \frac{1}{1+\exp(-(w_{k0} + \sum_{j=1}^p w_{kj}h_{nj}))}\]여기서 exp 란 exponential 의 약자로 자연상수e에 대한 지수함수를 의미한다, 즉 시그모이드 함수를 뜻한다.
각각의 $h$ 값 또한 마찬가지로 첫번째 신경망($net_j$) 에서 각 $h$ 로 향하는 $w$ 값의 곱을 더하면 각각의 $h$ 가 나온다.
\[h_{nj} = \frac{1}{1+\exp(-(w_{j0} + \sum_{i=1}^d w_{ji}x_{ji}))}\]이제 $o_{nk}$ 와 $h_{nj}$ 값을 합쳐서 Error Function 을 구하면 아래와 같은 식이 출력된다.
\[E_n(w) = \frac{1}{2}\sum_{k=1}^m\{t_{nk}-\frac{1}{1+\exp[-[w_{k0} + \sum_{j=1}^p w_{kj}(\frac{1}{1+\exp(-(w_{j0} + \sum_{i=1}^d w_{ji}x_{ji}))})]]}\}^2\]입력값 $x_{ji}$, 출력값 $t_{nk}$ 는 주어지기 때문에 각 $w$ 값을 변경해가면서 $E_n (w)$ 의 최소값을 찾으면 된다.
$E_n(w)$ 를 미분하여 도함수를 구하는 일은 굉장히 어렵기에
각 $w$의 대한 기울기값 $f’(E_n)$ 를 구해 경사하강법을 통해 최소값을 찾아나가야 한다.
기울기는 각각의 $w$값, $w_{jk}$ 에 대하여 Error Function 의 편미분 값으로 구한다.
\[\Delta w_{kj} = -a \frac{\partial E_n}{\partial w_{jk}}\]원활한 수식보기를 위해 $net_k$ 로 치환 $net_k = (w_{k0} + \sum_{j=1}^p w_{kj}h_{nj})$ $o_{k} = \frac{1}{1+\exp(-net_k)}$
약간의 편법(체인룰)을 사용하여 아래와 같은 식으로 변경
\[\frac{\partial E_n}{\partial w_{jk}} = \frac{\partial E_n}{\partial net_k} \cdot \frac{\partial net_k}{\partial w_{jk}} = \frac{\partial E_n}{\partial o_k} \cdot \frac{\partial o_k}{\partial net_k} \cdot \frac{\partial net_k}{\partial w_{jk}}\]마지막 부분 $\frac{\partial net_k}{\partial w_{jk}}$ 는 다른 $w$ 들은 모두 생략되고 특정 가중치 $w_{jk}$ 만 살아남기 때문에 아래처럼 $h_{nj}$ 로 변경된다.
\[\frac{\partial E_n}{\partial w_{jk}} = \frac{\partial E_n}{\partial net_k} \cdot \frac{\partial net_k}{\partial w_{jk}} = \frac{\partial E_n}{\partial o_k} \cdot \frac{\partial o_k}{\partial net_k} \cdot h_{nj}\]$\frac{\partial E_n}{\partial o_k}$, $\frac{\partial o_k}{\partial net_k}$ 에 대해서도 편미분값을 구하면 아래처럼 담백해진다.
$o_k$ 에 대해서만 남기때문에 Sumation 이 사라진다.
\(\begin{aligned}
\frac{\partial E_n}{\partial o_k} &= \frac{\partial}{\partial o_k} \frac{1}{2}\sum_{k=1}^m(t_{k}-o_{k})^2 \\&= -(t_k-o_k), \\ \ \\ \ \\
\frac{\partial o_k}{\partial net_k} &= \frac{\partial}{\partial net_k} \frac{1}{1+\exp(-net_k)} \\
&= \frac{-(-\exp(-net_k))}{(1+\exp(-net_k))^2} \\
&= \frac{\exp(-net_k))}{(1+\exp(-net_k))^2} \\
&= \frac{1}{1+\exp(-net_k)} \frac{\exp(-net_k))}{1+\exp(-net_k)} \\
&= o_k(1-o_k)
\end{aligned}\)
최종적으로 $hidden$ 과 $output$ 사이의 $o_k$ 를 향하는 각 $w$ 에 대한 기울기 값과 step size 식을 아래와 같은 식으로 구할 수 있다.
\[\Delta w_{kj} = -a \frac{\partial E_n}{\partial w_{kj}} = a \cdot (t_k-o_k) \cdot o_k(1-o_k) \cdot h\]마찬가지로 $input$과 $hidden$ 의 $w_{ji}$ 에 대해서도 경사하강법을 통해 기울기, step size 식을 구해야 한다.
\(\Delta w_{ji} = -a \frac{\partial E_n}{\partial w_{ji}}\)
이전과 같이 식을 편미분 하여 아래와 같이 식 을 간단화
\[\begin{aligned} \frac{\partial E_n}{\partial w_{ji}} &= \frac{\partial E_n}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}} \\ &= \frac{\partial E_n}{\partial net_j} x_i \\ \ \\ \frac{\partial E_n}{\partial net_j} &= \frac{\partial}{\partial net_j} \frac{1}{2} \sum_{k=1}^m (t_{k}-o_{nk})^2 \\ &= \frac{1}{2} \sum_{k=1}^m \frac{\partial (t_{k}-o_{nk})^2}{\partial net_j} \end{aligned}\]$\frac{\partial (t_{k}-o_{nk})^2}{\partial net_j}$ 만 때어놓고 봐 보면 아래처럼 변경 가능하다.
\[\begin{aligned} \frac{\partial (t_{k}-o_{nk})^2}{\partial net_j} &= \frac{\partial h_j}{\partial net_j} \cdot \frac{\partial net_k}{\partial h_j} \cdot \frac{\partial o_k}{\partial net_k} \cdot \frac{\partial (t_{k}-o_{nk})^2}{\partial o_k} \\\\ \frac{\partial h_j}{\partial net_j} &= h_j(1-h_j) \\\\ \frac{\partial net_k}{\partial h_j} &= w_{kj} \\\\ \frac{\partial o_k}{\partial net_k} &= o_k(1-o_k) \\ \\ \frac{\partial (t_{k}-o_{nk})^2}{\partial o_k} &= -2(t_k - o_k) \\ \end{aligned}\]최종척으로 아래와 같은 식이 도출된다.
\[\frac{\partial (t_{k}-o_{nk})^2}{\partial net_j} = -2h_j(1-h_j) w_{kj} o_k(1-o_k) (t_k - o_k) \\ \ \\ \begin{aligned} \frac{\partial E_n}{\partial net_j} &= \frac{1}{2} \sum_{k=1}^m \frac{\partial (t_{k}-o_{nk})^2}{\partial net_j} \\ &= -\sum_{k=1}^m h_j(1-h_j) w_{kj} o_k(1-o_k) (t_k - o_k) \\ &= -h_j(1-h_j)\sum_{k=1}^m w_{kj} o_k(1-o_k) (t_k - o_k) \\ \end{aligned}\]최종적으로 아래와 같은 식으로 $w_{ji}$ 의 기울기, step size 식을 구할 수 있다.
\[\begin{aligned} \Delta w_{ji} &= -a \frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}} = -a \frac{\partial E_n}{\partial net_j} x_i \\ &= -a(-h_j(1-h_j)\sum_{k=1}^m w_{kj} o_k(1-o_k) (t_k - o_k)) x_i \\ &= ah_jx_i(1-h_j)\sum_{k=1}^m w_{kj} o_k(1-o_k) (t_k - o_k) \end{aligned}\]$hidden$과 $output$ 사이의 $\Delta w_{kj}$, $input$과 $hidden$ 사이의 $\Delta w_{ji}$ 를 모두 구하였다.
- w 임의 설정
- 입력 - 은닉 - 출력 층 형성 및 선형 결합
- 은닉층과 출력층 사이의 $w_{kj}$ 값을 업데이트
- 입력층과 은닉층 사이의 $w_{ji}$ 값을 업데이트
에러가 충분히 줄어들 때 까지 이를 반복하는 것이 Back Propagation 알고리즘이다.
위 예제는 데이터 셋 하나에 대하여 각 $w$ 의 경사하강법을 통해 오차값을 줄였지만 대부분 수많은 데이터셋이 존재함으로 $\sum_{n=1}^N$ 수식이 앞에 하나씩 붙는다 생각하면 된다.
만약 net 이 하나씩 늘어날때 마다 연산과정도 기하급수적으로 늘어나고 과정도 많이 반복될 것이다.
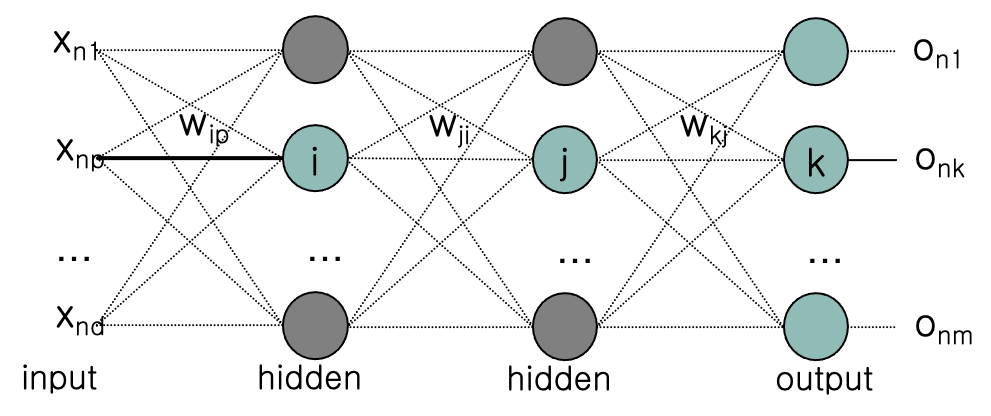
input node 10개, 각 layer node 10개, output 10개 인 네트워크가 위처럼 3개 있다면
$(10 \times 10) \times 3$ 개 이다 (가중치가 300개)
최근 대부분의 뉴럴넷 모델, CNN, RNN 등은 일반적으로 네트워크 100개 정도로 구성되어 있다.
역전파 알고리즘 실제 계산
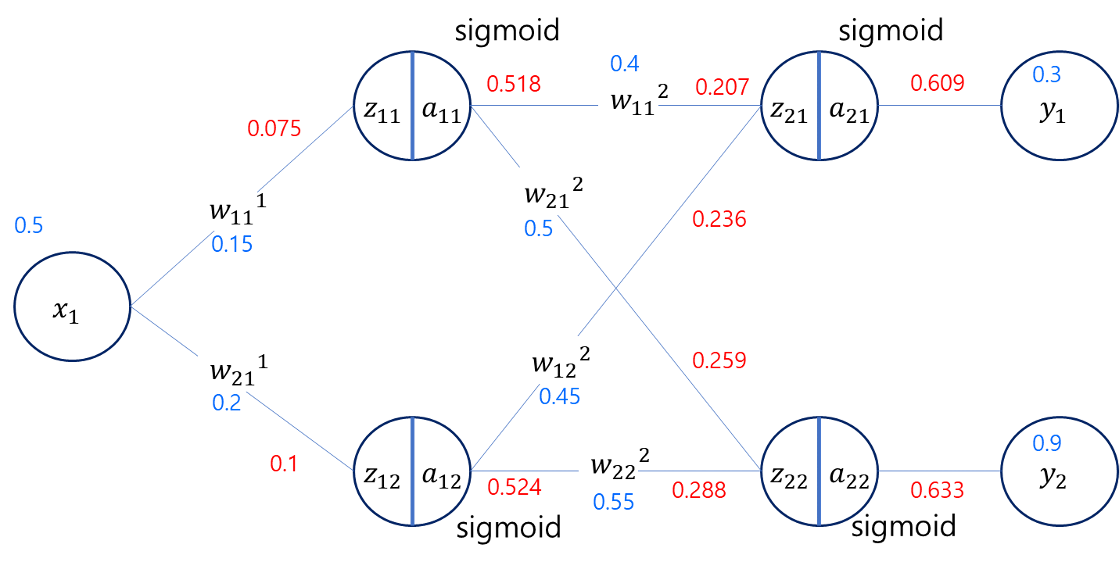
위와같은 뉴럴넷 모델에 임의의 w 값드이 정해져 있다면 Error Function(오차함수)의 결과는 아래와 같다.
\(E=\frac{1}{2} \sum(target - output)^2 \\
=\frac{1}{2}[(0.3−0.609)^2+(0.9−0.612)^2]=0.087\)
우리의 목적은 Error Function 의 결과값을 $w$ 조절을 통해 최대한 줄여나가야 한다.
\[\Delta w_{kj} = -a \frac{\partial E_n}{\partial w_{kj}} = -a \frac{\partial E_n}{\partial o_k} \cdot \frac{\partial o_k}{\partial net_k} \cdot h_{nj} \\ = a \cdot (t_k-o_k) \cdot o_k(1-o_k) \cdot h_{nj}\]$h$ 는 특정 노드의 결과값
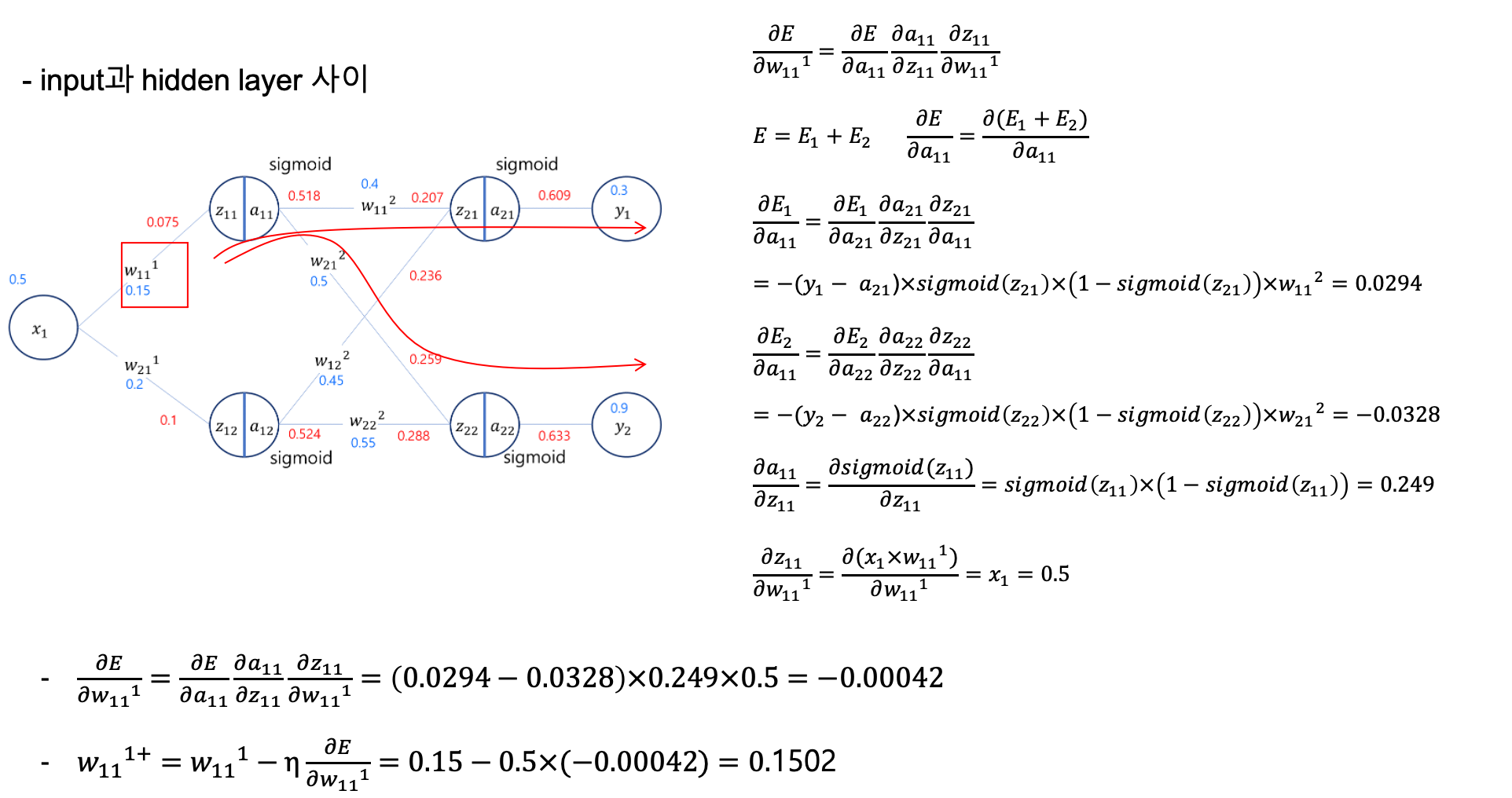
위의 경사하강법 공식을 사용해서 $net_2$ 에 해당하는 가중치 $w_{11}^2$ 의 값을 조절해보자.
위 공식대로라면 $t_k = y_1, o_k = a_{21}, w_{kj} = w_{11}^2, net_k = z_{21}, h_{nj}=a_{11}$ 이라 할 수 있다.
$net_k$ 에 해당하는 $z_{21}$ 의 값은
경사하강법 공식에 대입하면
\[\begin{aligned} \Delta w_{11}^2 = &a \cdot (y_1 - a_{21}) \cdot a_{21} (1 - a_{21}) \cdot a_{11} \\ = &a \cdot (0.3−0.609)×0.609×(1−0.609)×0.518 \\ = &a \cdot 0.0381 \end{aligned}\]만약 학습률 $a=0.5$ 라고 했다면 다음 경사하강법으로 구하게된 다음 $w_{11}^{2+}$ 은 아래와 같다.
\[w_{11}^{2+} = w_{11}^{2} - \Delta w_{11}^2 = 0.4 -0.5 \cdot 0.0381 = 0.380\]이번에는 $w_{11}^1$ 에 대해서 역전파 알고리즘 + 경사하강법 으로 값을 수정해보자.
\[\Delta w_{11}^1 = -a \frac{\partial E}{\partial w_{11}^1} = -a \frac{\partial E}{\partial a_{11}} \cdot \frac{\partial a_{11}}{\partial z_{11}} \cdot \frac{\partial z_{11}}{\partial w_{11}^1}\]$w_{11}^2$ 의 경우 $y_1$ 에 대해서만 영향을 끼치지만 $w_{11}^1$ 은 $y_1, y_2$ 모두 영향을 끼친다.
따라서 위의 Error 는 하나가 아닌 두개 에러의 합인 $E = E_1 + E_2$ 로 나타낸다.
\[\Delta w_{11}^1 = -a \frac{\partial (E_1+E_2)}{\partial w_{11}^1}\]각각의 E 에 대하여 편미분을 구하는 공식을 아래처럼 변경할 수 있다.
\(\frac{\partial E_1}{\partial a_{11}} = \frac{\partial E_1}{\partial a_{21}} \cdot \frac{\partial a_{21}}{\partial z_{21}} \cdot \frac{\partial z_{21}}{\partial a_{11}}\) \(\frac{\partial E_2}{\partial a_{11}} = \frac{\partial E_2}{\partial a_{22}} \cdot \frac{\partial a_{22}}{\partial z_{22}} \cdot \frac{\partial z_{22}}{\partial a_{11}}\)
이 부분도 7주차에 했던 편미분식의 반복이다.
Batch, Mini Batch
학습의 과정은 아래와 같다.
순전파 -> Error Function 흭득 -> 역전파 -> 가중치 조절
Epoch: 전체 데이터 셋에 대하여 순전파 후 역전파 한 횟수
일전에는 Epoch 를 여러번 반복하여 가중치를 조절하는 Batch 방식을 사용해 왔다.
모든 데이터셋 오차함수에 대해 한번에 가중치 조절하는 하게되면 비효율적이라는 생각에서 이런 비효율적인 계산 과정을 줄이고자 Mini Batch 라는 개념이 나왔다.
Mini Match: 데이터셋을 n 개의 그룹으로 나누어 순전파 하고 역전파 하는 것.
N 개의 데이터 셋이 있을때 이를 m개수를 가진 n 개의 그룹으로 나눈다면 $n = int(\frac{N}{m})$ 공식일 것
\[FP(g_1) \rArr BP(g_1) \\ FP(g_2) \rArr BP(g_2) \\ ... \\ FP(g_n) \rArr BP(g_n)\]마찬가지로 $g_1 ~ g_n$ 까지 1 Epoch 로 본다.
Mini Batch 의 경우 그룹화하고 바로바로 역전파가 이루어지기 다음 그룹에선 좀더 좋은 환경? 에서 다시 순전파, 역전파 과정이 이루어 지기 때문에 좀더 빠른 속도로 오차함수를 0으로 수렴하게 할 수 있다.
Mini Batch 방식에서 중요한 점이 하나 있는데 그룹화 시에 모집단에서 그룹별로 고르게 표본을 그룹화해야 한다.
SGD(Stochasitc Gradient Descent: 확률적 경사 하강법)
Mini Batch 의 데이터 수를 1로 설정, 데이터를 random 하게 순회하며 순전파 후 바로 역전파를 수행함.
수렴 속도가 빨라 질 수 도 있지만 발산되어 버릴 수 도 있음.
데이터 분포가 좁을 수록 SGD, 넓을 수록 Batch 방식을 사용하는 것을 권장.
Overfitting
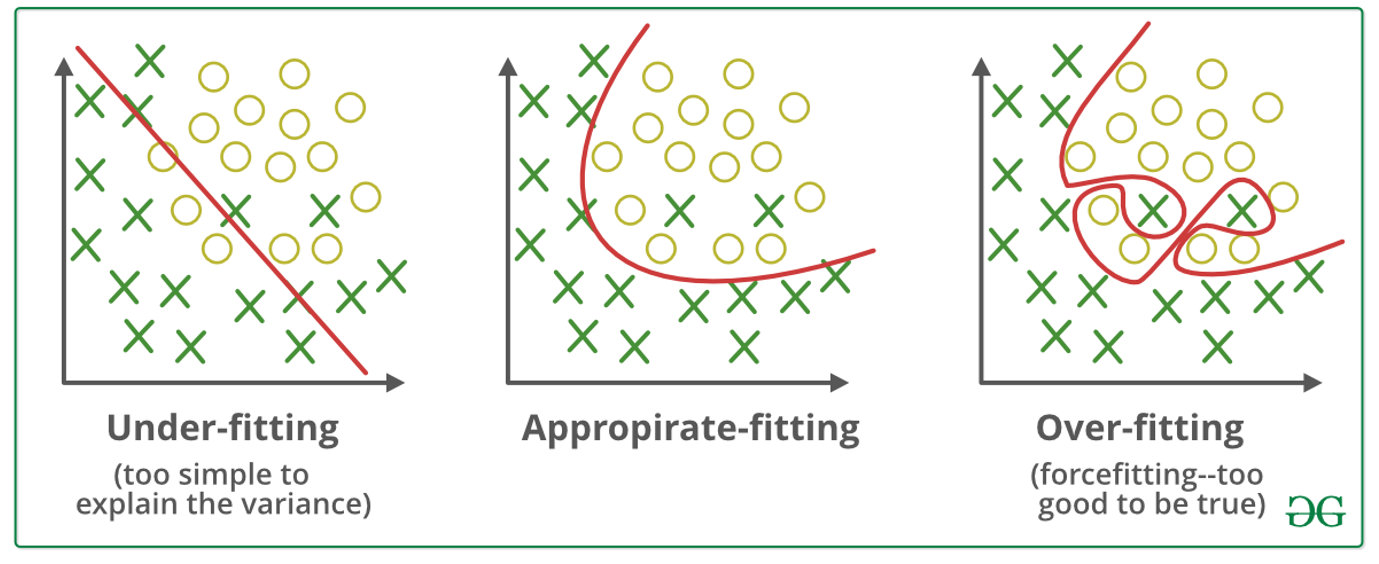
모든 머신러닝 모델에서 그렇듯이 NN 에서도 Overfitting 이 존재한다.
모든 training data set 에 대하여 Error Function 의 값이 0에 거의 수렴할때 까지 학습을 돌리면
위처럼 제공된 training data set에 대해서는 100% 분류가 가능하다.
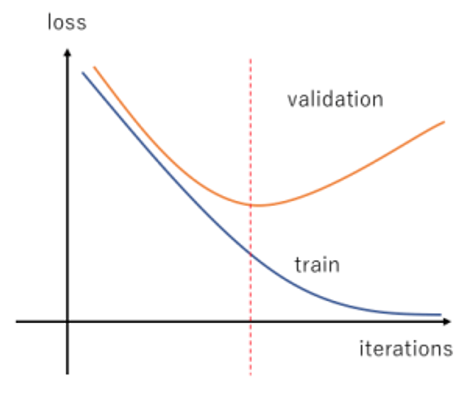
하지만 training data set 과 validation data set 2개로 분기하여 검증을 진행하게 되면 특정 시점부터는 validation data set 의 오차가 커지게 된다.
해당 시점이 Overfitting 이 생기는 시점이라 볼 수 있다.
만약 training data set 이 현실세계의 모든 상황의 모집단이라 할 수 있다면 발생된 Overfitting 이 항상 진실이라 할 수 있겠지만 대부분의 training data set 은 모집단의 일부일 뿐, 모든 상황을 대처할 순 없다.
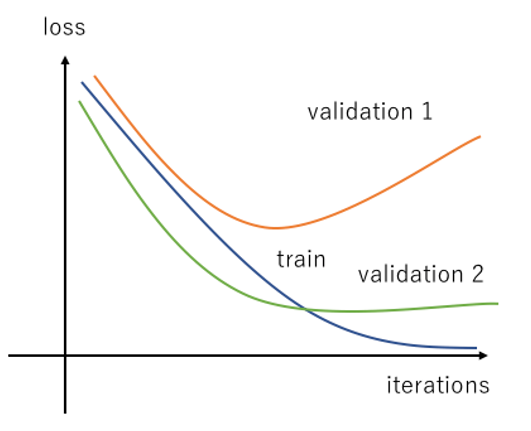
validation data set 또한 모든 모집단을 표현하는 것이 불가능 하기는 마찬가지이다.
위 그림처럼 validation data set 의 표본의 분포 편향에 따라서 Overfitting 이 언제 일어날 지 결정된다.
일반적으로 그나마 정확한 Overfitting 시점을 알아내기 위해 데이터를 3개로 쪼갠다(모든 머신러닝 모델이 비슷함)
- training data set: 학습용 데이터
- validation data set: 검증용 데이터
- test data set: 최종 성능 시험 데이터
모든 data set 의 데이터 분포가 고르게 되도록 노력해야 한다.
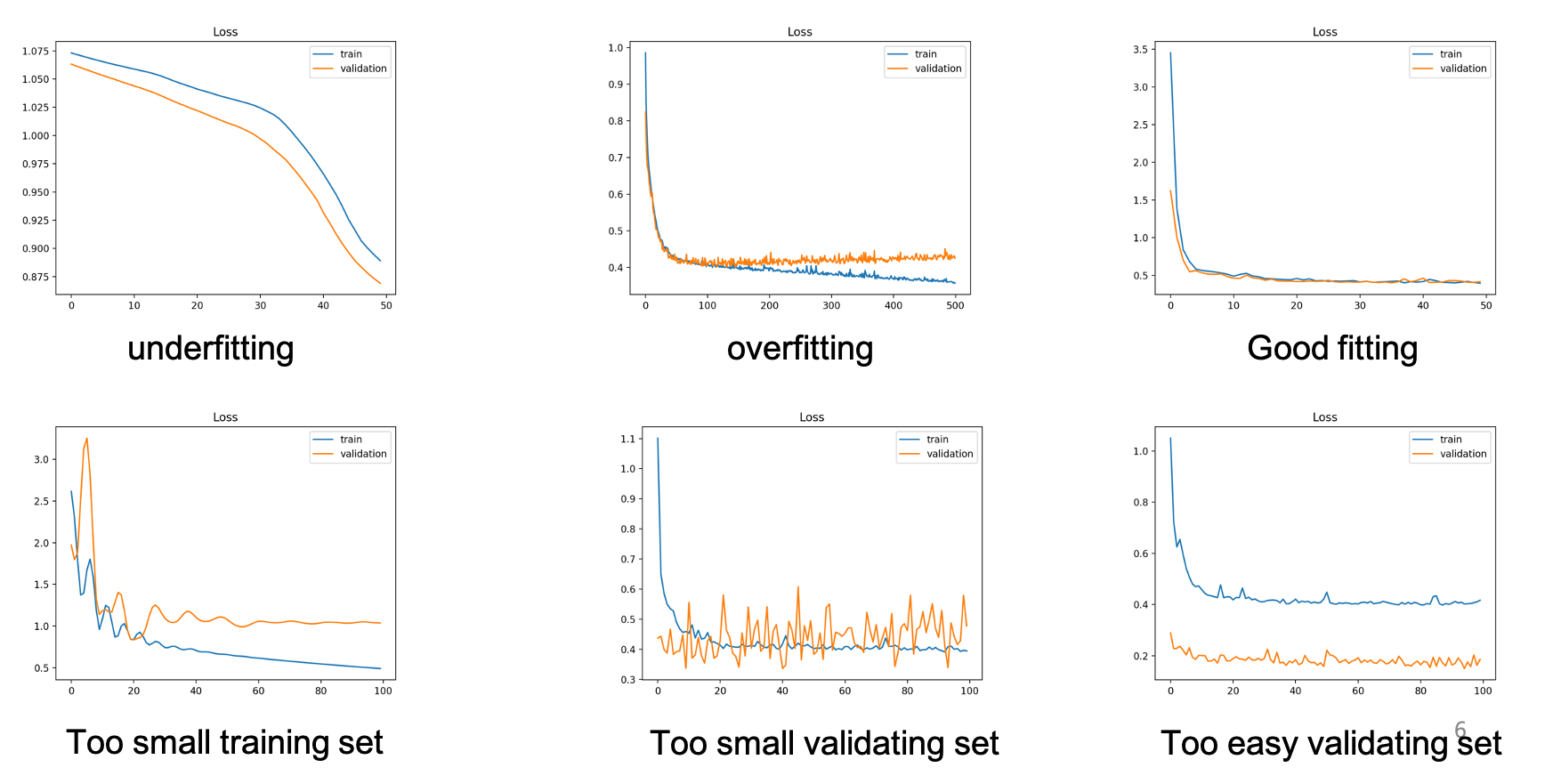
x 축은 epoch 수, y 축은 Error Function 의 결과값이다.
파랑계열이 traning data set 주황계열이 valiation data set
각각의 그래프를 보고 data set 이 잘못되었는지 epoch 수를 조절하는 것을 결정(early stop)할 수 있다.
Good Fitting 이 최적의 traning data set 과 validation data set 의 그래프, 어느정도 같이 0에 수렴하는 형태
출렁이는(fluxation) 그래프는 일반적으로 데이터 셋이 부족하다는 뜻.
Overfitting 방지
인공지능 모델 생성시 데이터를 수집하고 pre processing 하는 데 90% 이상의 자원이 사용된다.
Overfitting 이 일어나는 대부분의 경우는 데이터 부족으로 인해 모집단의 분포가 기울어져 있기 때문이다.
Overfitting을 막기위한 여러가지 방법론들이 개발되어 있다.
Cross Validation
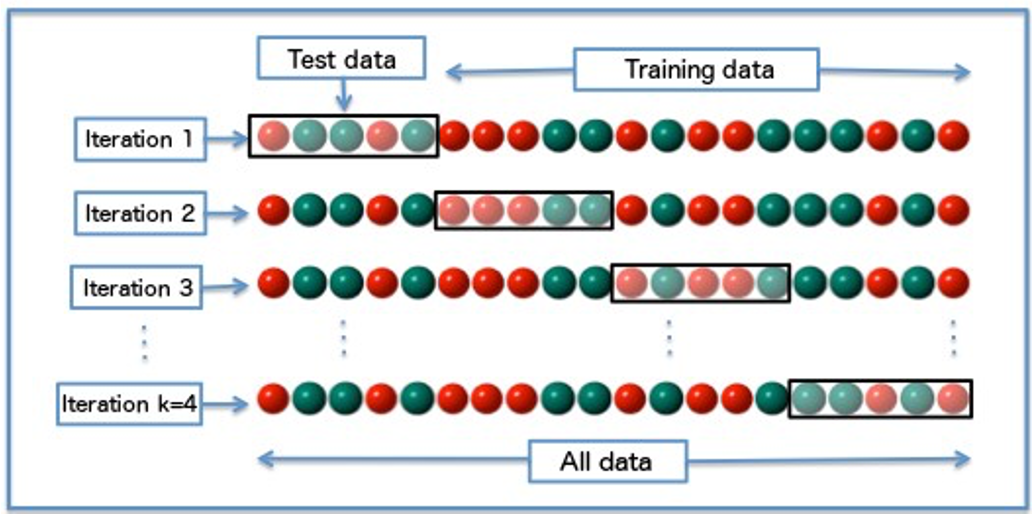
Epoch 마다 validation, traning 데이터 셋을 서로 교차해가면서 학습시키는 것
작은 데이터 셋에 너무 익숙해지지 않도록 계속 validation, traning 데이터 셋을 변경해가면서 진행하고 데이터 셋이 적을때 더욱 유용하다.
Early Stop
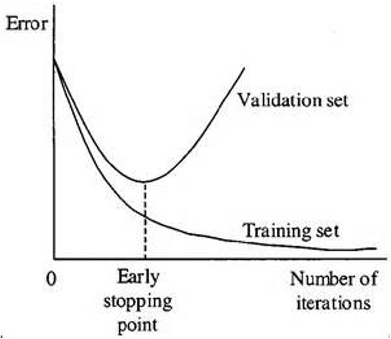
Overfitting 되기전에 멈추어 버리는것, 굉장이 많이 사용됨
Prunning
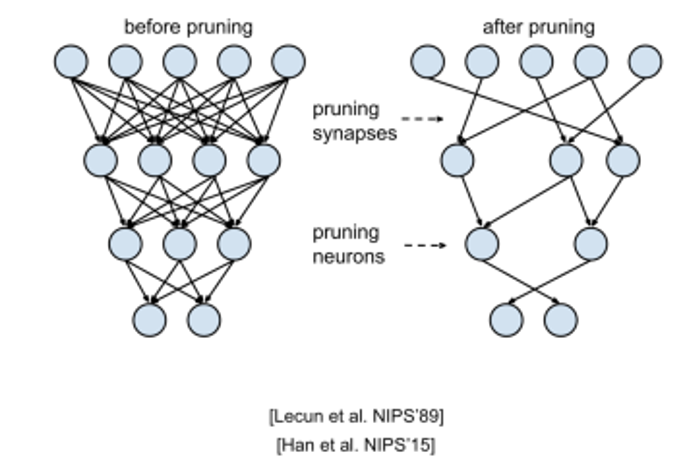
데이터 분류에 크게 관여하지 않는 노드들을 삭제
가중치가 매우 작다면 없애버리는 식으로 진행할 수 도 있다.
하드웨어적으로 뉴럴 링크 모델을 구현한 칩을 만들때 라인 하나하나가 모두 비용임으로 단순 Overfitting 만을 위한 것이 아닌 비용절감을 위해서도 사용하기도 한다.
Regularization (규제)
\[E = \sum E_n + \lambda\sum w^2\]기존에는 $E_n$ 에 합을 줄이기 위해서만 Epoch 를 반복했지만
여기에 모든 가중치 제곱의 합또한 더하여 Error Function 을 구성한다.
w 의 값도 너무 커지지 않도록 조절(규제)하면서 Error Function 값을 줄어나간다.
Droup Out
랜덤하게 노드를 선택하여 삭제
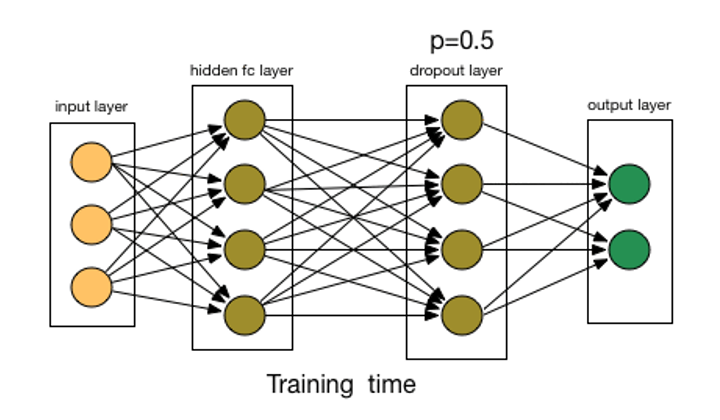
droupout layer 를 두고 $p = 0.5$ 랜덤하게 절반은 삭제후 weight 값을 업데이트 해 나간다.
데이터 셋에 익숙해지지 못하도록 모델을 바꾸어 버린다.
데이터를 바꾸거나, 모델을 바꾸는 방법으로 Overfiting 을 방지한다.
현재 Overfitting 방법론중 가장 많이 사용되는 방법이다.
Remove Features
분류에 크게 기여하지 못하는 feature 들을 제외
Ensembling(조합)
Bagging(Bootstrap Aggregation)
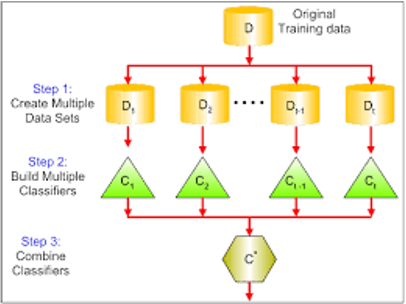
여러개의 데이터넷을 별도로 학습하여 독립적으로 출력된 모델들을 조합하여 사용하는 것.
여러개의 데이터셋으로 하나의 모델을 만드는 것이 아닌
여러개의 데이터셋으로 여러개의 모델을 만들고 각 모델의 결과를 조합(평균, 과반수) 하여 최종 결과를 도출하는 것.
Bosting
여러개의 모델을 별도로 학습하여 직렬적으로 조합하여 분류결과를 출력하는 것.
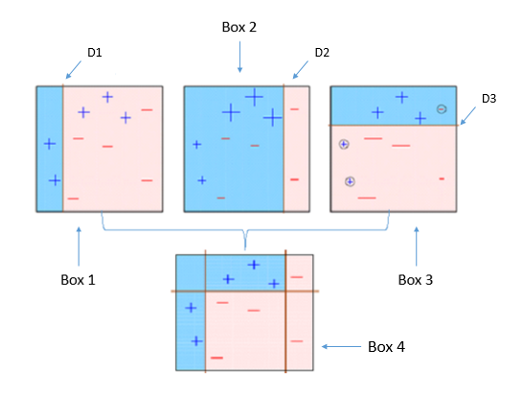
Bagging 과 다르게 각 모델을 직렬적으로 합쳐서 최종 분류결과를 도출한다.
Vanishing Gradiant
sigmoid activate function 를 사용하면 Vanishing Gradiant 문제가 발생한다.
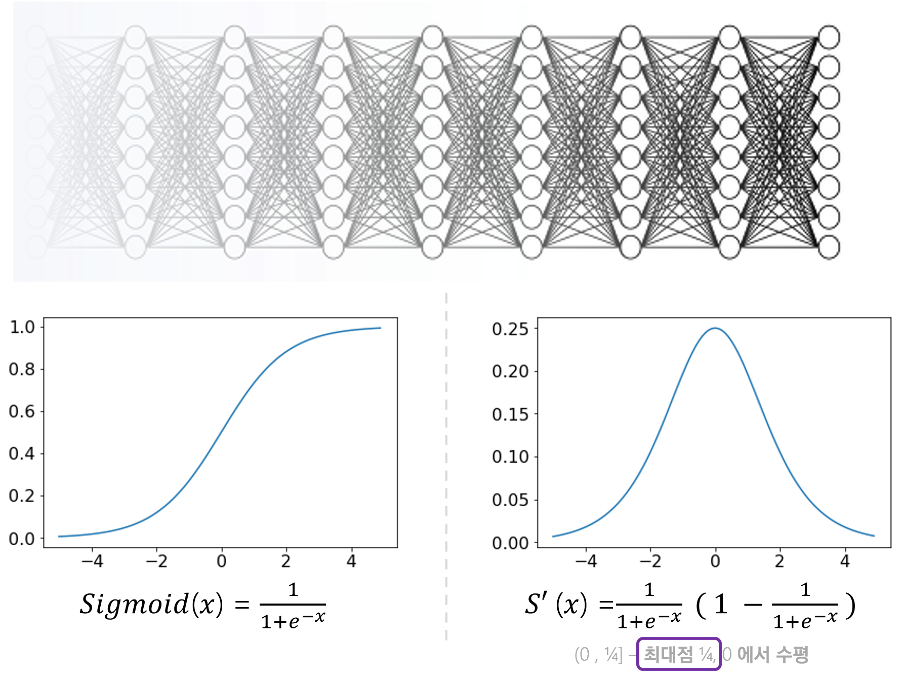
역전파 과정에서 가중치값들을 수정해 나가다 보면 input 노드에 가까워 질 수 록 미분을 지속적으로 해주어야 한다.
시그모이드 함수의 미분은 $sigmoid \cdot (1-sigmoid)$ 값인데 위 그래프처럼 미분 그래프의 maximum 값은 0.25 이다.
input 노드에 가까운 가중치는 거의 모든 output 노드에 영향을 끼치는 중요한 값인데 sigmoid 의 미분을 통해 경사하강법의 기울기값이 너무 적어지는 Vanishing Gradiant 문제가 발생한다.
Rectified Linear Unit(ReLU: 정류 선형 유닛)
Vanishing Gradiant 문제를 해결하기 위한 activate function 이 여러가지 있다.
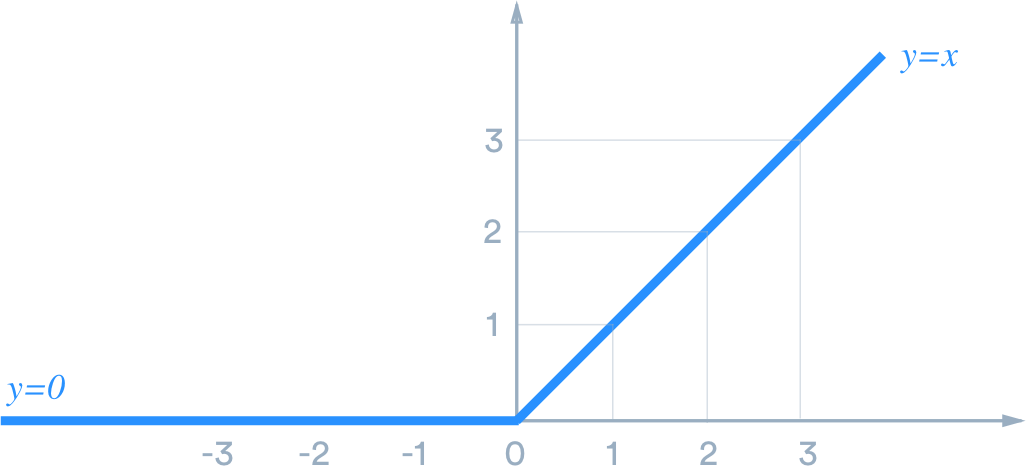
0 이하의 경우 모든 미분값은 0, 그 이외에는 모든 미분값은 1이다.
ReLU 를 사용하면 Vanishing Gradiant 는 해결되지만 모든 노드가 activation 되지 않는 단점이 있다.
sigmoid 의 경우 어떠한 $(input * w)$ 값이 들어와도 0 이상의 값이지 0 이 되진 않기에 모든 노드가 작은 값이긴 하더라도 항상 active 상태이다.
반면 ReLU 는 0 이하라면 바로 unactive 되기 때문에 굉장히 빠른 계산속도를 제공한다.
하지만 Knock out problem 이 존재한다.
이전 iteration보다 매우 큰 입력 값이 들어올 경우 대부분의 노드에서 ReLU activated 역전파 과정에서 큰 업데이트(감소방향으로) 발생 다음 iteration에서 많은 노드가 activate되지 않음 역전파 과정에서 update 되지 않음 학습과정에서 다시는 업데이트 되지 않음
Vanishing Gradiant 을 해결하기 위한 다른 activate function 또한 많이 개발되어있다.
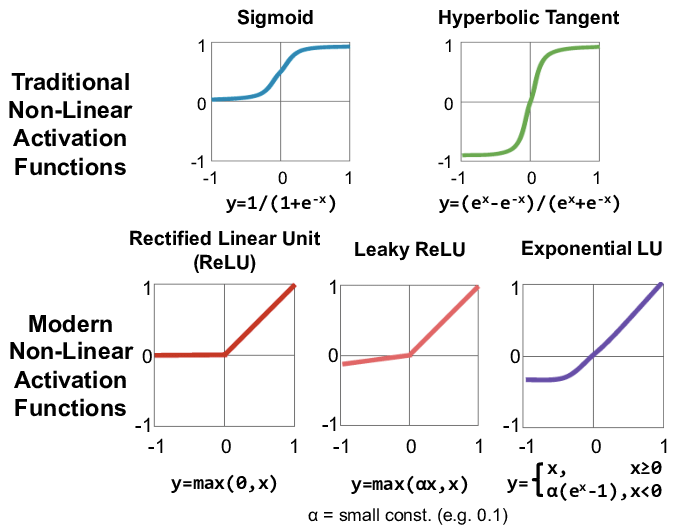
데이터, 모델의 성격에 따라 여러가지 activation function 을 사용할 수 있다.