Support Vector Machine(SVM) 개요
https://angeloyeo.github.io/2020/09/30/SVM.html https://www.youtube.com/watch?v=qFg8cDnqYCI
뉴럴넷이 활성화 되기 전 가장 유명하고 자주 사용되었던 기계학습 이론
뉴럴넷에 비해 SVM 은 수학적으로 설명 가능한 모델이다.
최적의 솔루션 결과를 도출하기 위한 수학적 설명, 입증이 가능하다.
classify 에서 2가지 방법으로 나누었을때 어떤 방식이 더 잘 나눈 방식인지 물어본다면 우측이라 할 수 있다.

분리선의 boundary 를 늘릴 수 있을 때 더 넒은 범위를 가지는 모델이 더 좋다 말할 수 있다.
SVM 기본컨셉이 바로 더 넓은 범위의 폭(max-margin) 을 가지는 분리선을 구하는 것이다.
Hyperplan
데이터를 두개의 집단으로 나누는 모형
데이터의 차원(n)보다 낮은(n-1) 차원의 평면을 이용해 classify
max-margin 을 가지는 최적의 Hyperplane 을 찾는다는 것이 목표이다.
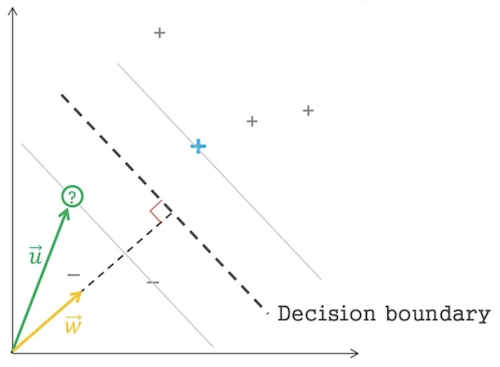
이미 Hyperplane 과 수직인 벡터 $\mathrm{\vec{w}}$ 을 알고 있을 때
데이터를 [+, -] 로 classify 하는 조건식을 내적의 길이를 특정상수와 비교하는 식으로 표현할 수 있다.
$\mathrm{\vec{w} \cdot \vec{u} > c}$
식을 약간 변경해서 아래처럼 변경한다.
$\mathrm{\vec{w} \cdot \vec{u} +b \ge 0 }$
참일경우
-, 거짓일 경우+
이것이 HyperPlane 의 기본 식이라 할 수 있다.
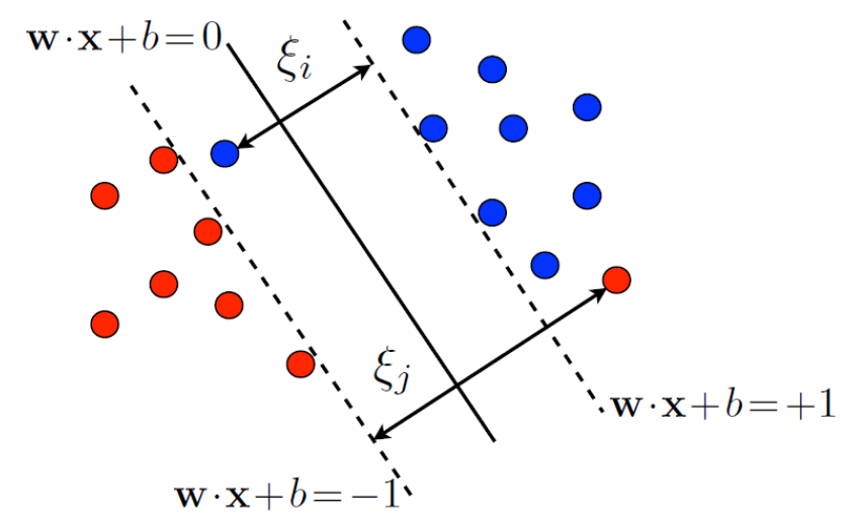
Hyperplane 앞뒤 plane 을 Plusplane, Minusplane 으로 표현하여 아래 그림처럼 표기할 수 있는데
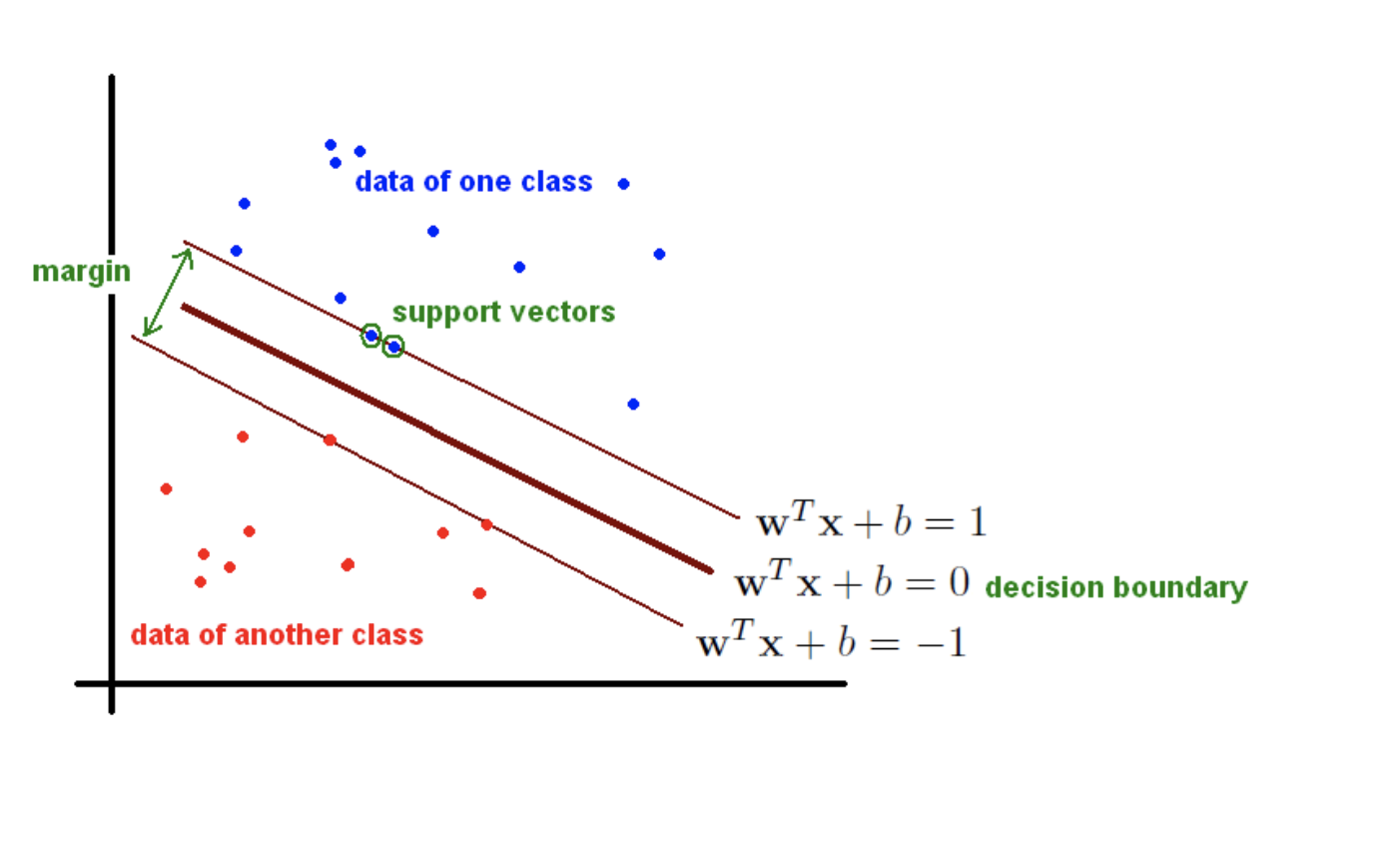
궁극적인 목표는 max-margin 을 가지는 법선벡터 $\mathrm{\vec{w}}$, 그에따른 상수 $b$ 를 찾는것이다.
1 , -1는 bias 를 조절해 다른값으로 만들 수 있기 때문에 편의상1, -1로 설정하였음
내적은 두 백터의 행렬 곱셉으로 식을 표현
각 데이터들의 관계식을 Plusplane, Minusplane 으로도 표기할 수 있다.
\[\vec{w} \cdot \vec{x}^+ + b \ge 1 \\ \vec{w} \cdot \vec{x}^- + b \le 1\]$x^+$ 는 Plusplane 위에 존재하는 Support vectors
$x^-$ 는 Minusplane 위에 존재하는 Support vectors
함수 $y_i$ 는 $\vec{x_i}$ 에 따라 +1 혹은 -1 을 출력한다 했을 때
함수 $y_i$ 를 사용해서 각 데이터들의 관계식을 하나만으로 표현할 수 있다.
음수를 곱하여 비교 표현식을 통일할 수 있다.
\[y_i (\vec{w} \cdot \vec{x_i} + b) \ge 1\]두식을 합친 식이 0이 될 때 Hyperplane 식이라 할 수 있다.
\[y_i (\vec{w} \cdot \vec{x_i} + b) -1 = 0\]MaxMargin
minus plane 에서 $\vec{w}$ 방향으로 실수$\lambda$ 배 만큼 이동한게 plus plane 이라 할 수 있다.
$\lambda$ 식을 $\vec{w}$ 관계식으로 표현할 수 있다.
\[\begin{aligned} w^T x^+ + b &= 1 \\ w^T (x^- + \lambda w) + b &= 1 \\ (w^T x^- + b)+\lambda { w }^{ T }w &= 1 \\ -1 + \lambda w^T w &= 1 \\ \lambda =\frac{2}{w^T w} \\ \end{aligned}\]Margin 을 구하는 공식역시 $\vec{w}$ 관계식으로 표현할 수 있다.
\[\begin{aligned} \mathrm{Margin}&=\mathrm{distance}(x^+, x^-) \\ &= \|x^+ - x^-\|_2 \\ &= \|(x^- + \lambda w) - x^-\|_2 \\ &= \| \lambda w \|_2 \\ &= \lambda \sqrt{w^T w} \\ &= \frac{2}{w^T w} \sqrt{w^T w} \\ &= \frac{2}{\sqrt{w^T w}} \\ &= \frac{2}{\|w\|_2} \end{aligned}\]우리가 구해야 할 것은 가장 큰 $\mathrm{Margin_{max}}$ 이기에
반대로 역수를 만들어 가장 작게 하는것 과 동일하다.
나중에 라그랑주 승수법에서 미분진행시 수학적 편의를 위해 제곱을 취해준다.
\[\min \frac{1}{2}{\|w\|_2^2}\]라그랑주 승수법
위에서 구한 HyperPlane 과 Margin 을 조건식과 목적식으로 사용
\[\begin{cases} \min & \frac{1}{2}{\|w\|_2^2} \\ \mathrm{s.t} & y_i (\vec{w} \cdot \vec{x_i}^+ + b) -1 = 0 \end{cases}\]라그랑주 승수법을 사용해 최적화 문제를 해결할 수 있게 되었다.
\[L_p(\vec{w},b,a_i) = \frac{1}{2}{\|w\|_2^2} - \sum_{i=1}^n a_i(y_i(\vec{w} \cdot \vec{x}_i +b)-1)\]라그랑주 승수 $\lambda$ 를 $a$ 로 표현
라그랑주공식에 따라 두 변수에 대한 편미분을 진행
\(\frac{\partial L}{\partial w} = 0 \\ \|w\|_2 - \sum_{i=1}^n a_i(y_i(\vec{x}_i)) = 0 \\ \|w\|_2 = \sum_{i=1}^n a_i(y_i(\vec{x}_i)) \\ \|w\|_2 = \sum_{i=1}^n a_i y_i \vec{x}_i\) \(\frac{\partial L}{\partial b} = 0 \\ -\sum_{i=1}^n a_i(y_i) = 0 \\ \sum_{i=1}^n a_i y_i = 0\)
그리고 라그랑주 공식에 대입하여 정리해나가면
\[\begin{aligned} &\frac{1}{2}{\|w\|_2^2} - \sum_i a_i(y_i(\vec{w} \cdot \vec{x}_i +b)-1) \\ &\to \frac{1}{2}w^Tw - \sum_i a_i y_i (w^T x_i +b) + \sum_i a_i \\ &\to \frac{1}{2}w^T \sum_i a_i y_i x_i - \sum_i a_i y_i w^T x_i - b\sum_i a_i y_i + \sum_i a_i \\ &\to \frac{1}{2} \sum_i a_i y_i w^T x_i - \sum_i a_i y_i w^T x_i - b\sum_i a_i y_i + \sum_i a_i \\ &\to -\frac{1}{2} \sum_i a_i y_i w^T x_i + \sum_i a_i \\ \end{aligned}\]\[\to -\frac{1}{2} \sum_i a_i y_i w^T x_i + \sum_i a_i \\ \to -\frac{1}{2} \sum_i a_i y_i (\sum_j a_j y_j x_j^T) x_i + \sum_i a_i \\ \to -\frac{1}{2} \sum_i \sum_j a_i y_i a_j y_j x_j^T x_i + \sum_i a_i \\ \to \sum_i a_i -\frac{1}{2} \sum_i \sum_j a_i y_i a_j y_j x_j^T x_i\]$\sum_{i=1}^n a_i y_i = 0$ 임으로 상수 b 는 생략된다.
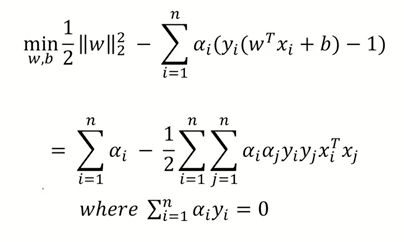
라그랑주 Primal
라그랑주 Primal 은 라그랑주식을 maxmize 하고 minimize 한 것.


최종적으로 라그랑지안 승수식을 maxmize 하고 minimize 한 식이
$f(W)$ 를 minimize 한 값과 일치하게 된다.
실제 우리가 구해야할 $\min\frac{1}{2}{(|w|_2)^2}$ 를 구하는 것과 같음으로 라그랑주 Duality 를 사용해 식을 변형한다.
라그랑주 Dual 은 라그랑주 식을 minimize 하고 maxmize 한 것.
TTK 조건이 성립하면 라그랑주 Primal 과 라그랑주 Dual 의 결과가 일치한다.
정리
또 $a_i$ 에 대한 조건이 하나 더 붙는데 $y_i(\vec{w} \cdot \vec{x}_i +b) -1$ 은 항상 0보다 크다 따라서 $L$ 을 minimize 하려면 $a_i$ 역시 항상 0보다 커야한다.
라그랑주 승수법에 조건에 따라 제약조건과 $\min$ 함수의 기울기 백터 뺄샘이 영백터가 되어야 함으로
$L$함수에서 $w$ 와 $b$ 에 대한 편미분의 결과가 모두 0 이 되어야 한다.
\(\frac{\partial L}{\partial w} = 0 \\ \rArr \vec{w} - \sum_{i=1}^na_iy_ix_i = 0 \\ \rArr \vec{w} = \sum_{i=1}^na_iy_ix_i\) \(\frac{\partial L}{\partial b} = 0 \\ \rArr \sum_{i=1}^na_iy_i=0\)
이제 제약조건상에서 $\vec{w}$ 에 대한 값과 $\sum_{i=1}^na_iy_i=0$ 이라는 사실을 알아냈다.
우리의 최종목표 $\min f(w) = \min\frac{1}{2}{(|w|_2)^2}$ 하는 값이 a 라그랑주 duality 와 ttk 조건하에 $a$ 이차식에서 $a$ 를 maxmize 하는 식으로 변경되었기 때문에 a 의 최대값을 구하는 문제로 변경된다.
a 의 최대값을 구했다면 이제 a 를 사용해

SVM Soft Margin