Reinforcement Learning(강화 학습)

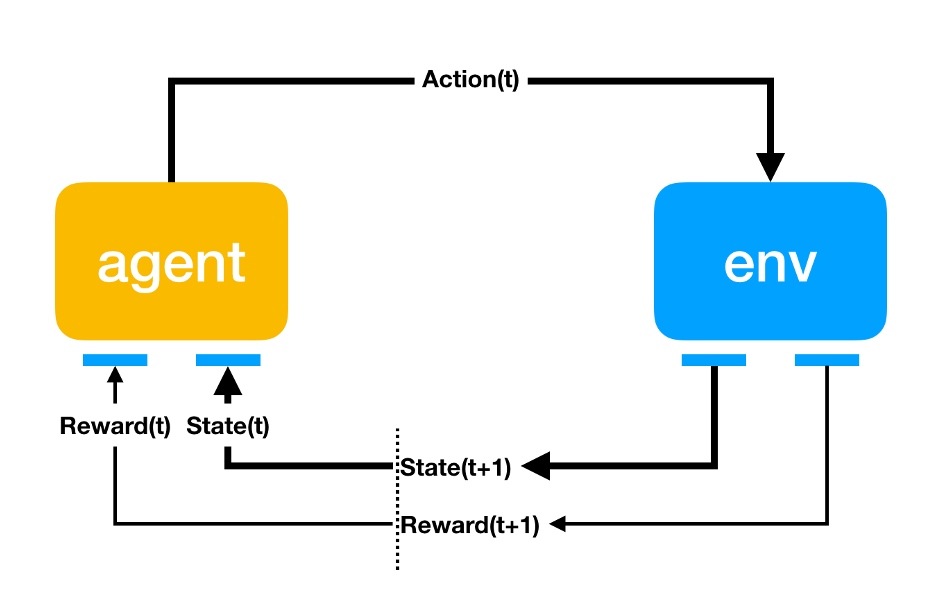
어떤 env(환경) 안에서 정의된 agent 가 현재의 State(상태) 를 인식, 선택 가능한 Action(행동) 들 중 Reward(보상) 을 최대화하는 행동 혹은 행동 순서를 선택하는 방법

게임 이론, 제어이론, 정보이론, 최적화, 통계학, 유전 알고리즘 등 다양한 분야 활용

어떤 경우에는 Reward 가 패널티가 될 수 도 있다

Markov Property (마르코프 속성)

현재를 알면 미래는 과거와 무관하다는 특성

아래 수식이 성립하는 경우 Markov Property (마르코프 속성) 이라 한다.

\[P[S_{t+1} | S_t] = P[S_{t+1} | S_1,\cdots,S_t]\]

$S_t$ 은 현재 State,
$S_{t+1}$ 은 바로 앞으로 일어날 미래 State

$S_1$ 부터 $S_t$ 까지 모든 상황이 일어난 상황에서 $S_{t+1}$ 이 일어날 확률과

$S_t$ 가 일어난 상황에서 $State_{t+1}$ 이 일어날 확률이 같을경우 Markov Property 이라 함

Markov Process

Markov Property 를 가지는 상태가 이어지는 상황을 Markov Process 라 한다.

ex) Markov Process 인 예 $S_t$ 상황에서 $10 를 가지고 있을 때 매번 $1 을 걸고 동전던지기 게임 진행할 경우
$S_{t+1}$ 상황은 $11 이 되거나 $9 가 될것으로 예측할 수 있다.
여기서 $S_{t+1}$ 를 예측하기 위해 왜 $S_t$ 상황이 $10 가 되었는지 이유는 전혀 알 필요가 없다.

ex) Markov Process 가 아닌 예 보자기에서 동전뽑기 같은 경우는 Markov Process 가 아니다.
100원 5개, 50원 5개, 10원 5개중 랜덤하게 6개를 뽑아 최종 가격을 예측할 때에는 과거에 어떤 동전을 뽑았는지 예측해야 정확한 결과를 얻을 수 있다.

Markov Process는 상태(State, S)와 상태 이행 확률(Probability, P)로 구성되며

$P$는 상태 $s$에서 $s’$으로 전이될 확률을 뜻한다.

Markov Property with Matrix

행렬로 간단하게 각 단계별 Markov Property 를 표현할 수 있다.

\[P = from\begin{bmatrix} p_{11} & \cdots & p_{1m} \\ p_{21} & \cdots & p_{2m} \\ & \cdots & \\ p_{n1} & \cdots & p_{nm} \end{bmatrix}\]

초기상태 $p_{11} \cdots p_{n1}$ 에서 최종 상태의 예측값 $p_{1m}\cdots p_{nm}$ 까지의 단계별 Markov Property 를 행렬로 표기할 수 있다.

ex)

실제 예를 그래프와 행렬로 표현하였다.

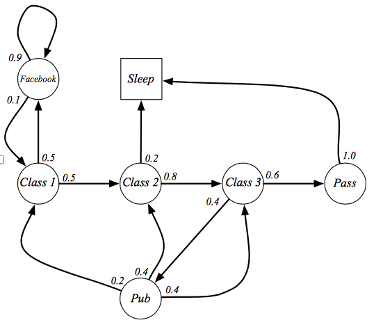
$p(C1|C1)$ 부터 $p(Sleep|Sleep)$ 까지 행렬이 있으며 state 가 이어진 여러개의 episode 가 생성될 수 있다.

C1 C2 C3 Pass Sleep
C1 FB FB C1 C2 Sleep
C1 C2 C3 Pub C2 C3 Pass Sleep
C1 FB FB C1 C2 C3 Pub C1 FB FB
FB C1 C2 C3 Pub C2 Sleep

Markov Reward Process

기존 Markov Process 는 $S$ 와 $P$ 만 있었다면
Markov Reward Process 는 튜플로 구성되며 아래 4가지 요소가 존재한다.
tuple: $<S, P, R, \gamma>$

또한 각 요소별로 알아야할 수식들이 몇가지 존재한다.

probability matrix: $P_{ss’} = P[S_{t+1}=s’|S_t]$
현재상태 $s$ 가 $s’$ 로 전이될 확률 (위의 matrix에서 구할수 있다)
Reward Function: $R_s = E[R_{t+1} | S_t = s]$ 현재상태에서 얻을 수 있는 모든 Reward 의 평균(expactation)
discount factor(감쇠비): $\gamma \in [0,1]$

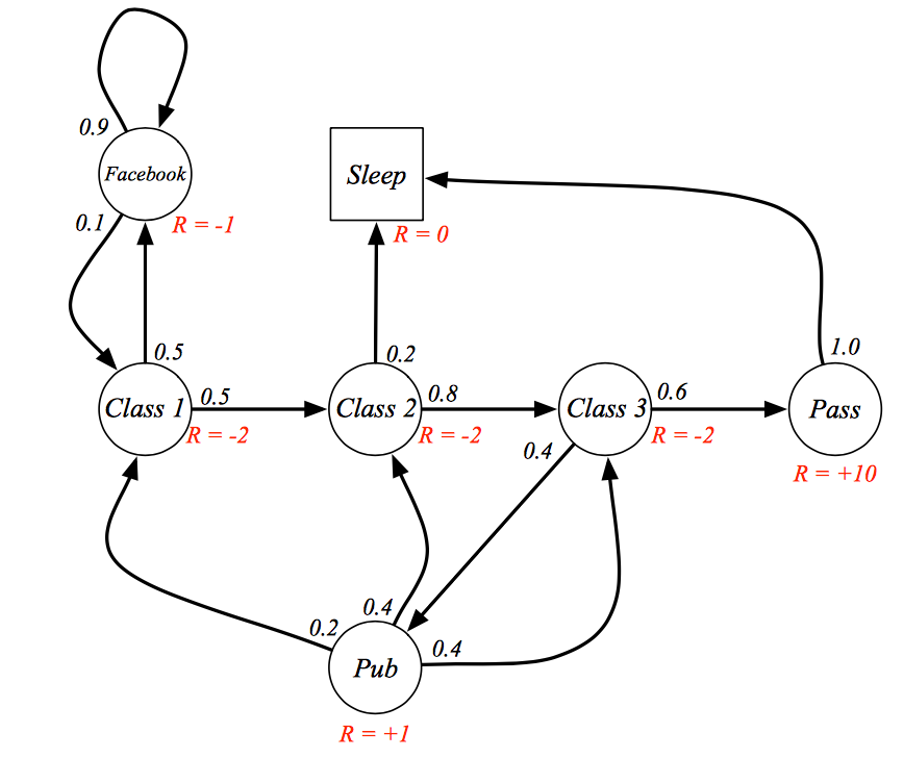
각 State 로 가는 단계에 Reward 를 추가

현 시점 $S_t$ 에서 받을수 있는 Reward 의 총합 Discounted Return($G_t$)은 아래와 같다.

\[G_t = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} = R_{t+1} + \gamma^1 R_{t+2} + \gamma^2 R_{t+3} + \cdots\]

process 가 언제 끝날 지 모르기 때문에 k 는 무한히 증가한다.
(위 경우도 cycle 이 구성되어 있기 때문에 무한대꼴이 나올 수 있음)

감쇠비 $\gamma$ 의 존재 이유는 현시점의 Reward 와 미래시점의 Reward 수치가 같더라도 가치는 다르기 때문

만약 위 그래프에서 모든 Reward 의 양수값이라면 $G_t$ 는 무한대가 되기에 이를 방지하기 위해서라도 감쇠비은 필요함

MRP Value Function (Bellman equation)

위 그래프에서 $G_t$ 는 어떤 프로세스로 흐르냐에 따라 달라지게 된다.

현 상태에서의 Discounted Return 의 평균(expactation)을 Value Function (Bellman equation)으로 부르며 아래와 같은 수식으로 표현한다.

\[v(s)=E[G_t|S_t=s]\]

state $s$ 에서 시작했을 때 얻을 수 있는 return 의 평균, 아래와 같이 재귀적으로 구성 가능하다.

식을 조금 더 풀어쓰면 아래와 같다.

여기서 $s$ 는 현상태, $s’$ 는 연결된 다음상태를 가리킨다.
$\begin{aligned} v(s)&=E[G_t|S_t=s] \\ &=E[R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3} + \cdots|S_t=s] \\ &=E[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \cdots)|S_t=s] \\ &=E[R_{t+1}+\gamma G_{t+1}|S_t=s] \\ &=R_s + \gamma \sum_{s' \in S} P_{ss'}v(s') \\ \end{aligned}$

다음 상황으로 이동할 확률 $P_{ss’}$ 과 해당 확률에서의 평균(기대값)을 재귀적으로 더한다.

재귀형식으로 구성되기 때문에 아래 그림처럼 트리로도 표현할 수 있다.

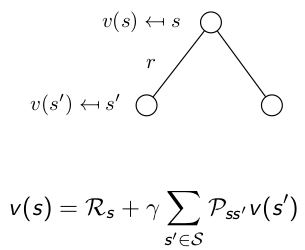
아래와 같이 행렬로도 표현할 수 있다.
$\begin{bmatrix} v(s_1) \\ \cdots \\ v(s_n) \end{bmatrix} = \begin{bmatrix} R(s_1) \\ \cdots \\ R(s_n) \end{bmatrix} + \begin{bmatrix} p(s_1|s_1) & \cdots & p(s_n|s_1) \\ \cdots & \cdots & \cdots \\ p(s_1|s_1) & \cdots & p(s_n|s_n) \\ \end{bmatrix} \begin{bmatrix} v(s_1) \\ \cdots \\ v(s_n) \end{bmatrix}$

value function 은 MRP 외에도 다른 value 기반 방법론에서도 계속 사용되니 숙지 필수

Markov Decision Process (MDP)

Markov Reward Process 애 Action 이 추가된 process

tuple: $<S, A, P, R, \gamma>$

기존에는 $s$ 에서 $s’$ 로 가는확률이 단순하게 지정되어 있었지만 Markov Decision Process 에서는 어떠한 Action 을 취해야 해당 $s’$ 으로 갈수 있는지도 정해져 있다.

Markov Decision Process 역시 알아야할 수식이 몇가지 있다.

probability matrix: $P^a_{ss’} = P[S_{t+1}=s’|S_t, A_t]$
현재상태 $s$ 가 $s’$ 로 전이될 확률 행렬
Reward Function: $R_s = E[R_{t+1} | S_t = s, A_t=a]$ 현재상태에서 얻을 수 있는 모든 Reward 의 평균(expactation)
Policy: $\pi(a|s) = P[A_t=a|S_t=s]$ 현재상태 $s$ 에서 액션 $a$ 를 취할 확률

MDP Value Function

아래 2가지 value function 이 존재한다.

State Value Function

$s$ 상태에서 특정 Policy $\pi$ 를 따라 고정된 $a$ 를 선택했을 때 Discounted Return 의 평균
$\begin{aligned} v_\pi(s) &= E_\pi[G_t|S_t=s] \\ &= E_\pi[R_{t+1} + \gamma v_\pi(S_{t+1})|S_t=s] \end{aligned}$

Action Value Function (Q function)

$s$ 상태에서 모든 액션집합을 선택했을 때 발생가능한 Discounted Return 의 평균

\[\begin{aligned} q_\pi(s,a) &= E_\pi[G_t|S_t=s, A_t=a] \\ &= E_\pi[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1})|S_t=s, A_t=a] \end{aligned}\]

Optimal State Value Function & Optimal Action Value Function

Action Value Function 의 경우 Action 선택에 따라 Value Function 의 값도 변화할 것이다.

그때 선택된 최대값의 Value Function 을 Optimal State Value Function, Optimal Action Value Function 이라 한다.

\[v_*(s) = \max_\pi v_\pi(s) \\ q_*(s) = \max_\pi q_\pi(s)\]

각 상태에서 Optimal Value Function 을 알 수 있다면 MDP 문제를 해결한 것 과 같다.
물론 이 최적화 함수를 찾기 위해 학습을 진행해야 한다.

Dummy Q Learning

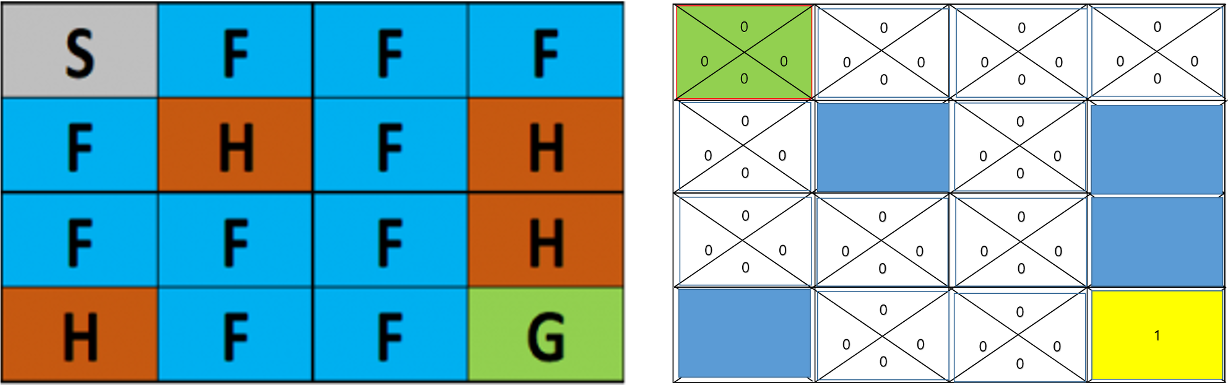
Frozon Lake 라는 MDP 문제를 해결하는 유명한 예제

S: Start
F: 얼어붙은 호수 (이동 가능)
H: Hole (이동 불가능)
G: Gole

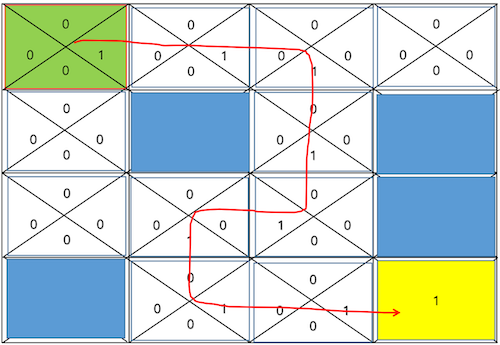
만약 누군가가 각 Action 마다 가장 큰 Reward 를 얻을 수 있는지 알려준다면

각 상황 $s$ 에서의 Optimal Action Value Function 를 알려준다면
$\pi_s(s)=argmax_a q(s,a)$

아래 그림과 같이 수월하게 길을 찾아갈 수 있다.

Environment 를 정확히 알 수 있다면 각 상황에서 Optimal Action Value Function 를 구할 수 있다.
여기서 Environment 는 (deterministic, finite states) 라고 표현하며 어떤 Action 을 했을때 어떤 Reward 가 오는지를 명확히 알 수 있는 것을 뜻한다.

select and execute action $a$ - 특정 액션 선택
receive immediate reward $r$ - 액션에 대한 보상 흭득
observe the new state $s’$ - 새로운 상태로 이동
Update the table entry for $\hat{q}*(s,a)$ as follows - 현재 상태의 추정 최적함수 수정, 수식은 아래와 같다.
$\hat{q}(s,a) \larr r+\max_{a’}\hat{q}⁡_(s’,a’)$

Bellman equation 을 참고하여 수식을 수정한다.

내용을보면 알겠지만 무식한 방법으로 계속 반복하면서 본인 앞의 연결된 상태중 가장 높은 Optimal Action Value 를 가진 쪽으로 이동하는 방식이다.

현재 구한 최적함수 $q_(s,a)$ 보다 더 나은 추정(hat) 최적함수 $\hat{q}_(s,a)$ 를 찾는 과정은 아래의 반복이다.

Exploit, Exploration (공적, 탐사) 알고리즘

문제는 위처럼 모든 Optimal Action Value 이 아직 정해지지 않아 0인 경우 랜덤하게 이동하면서 얻어 걸린 Action Value 가 Optimal Action Value 가 되버린다.

새로운 길을 Exploration 했을때 좀더 많은 Reward 가 얻어질 수 도 있지만 한번 정해진 Optimal Action Value 를 벗어나는 것은 불가능하게 된다.

E-greedy(Epsilon-Greedy)

이런 문제를 방지하기 위해 E-greedy 방법을 사요한다.

$\epsilon$ 값을 정하고 랜덤값이 해당 값보다 작으면 랜덤 아니라면 기존의 Optimal Action Value 를 따름으로서
새로운 길을 찾을 수 있는 Exploration 기회를 주는 방식이다.

# ϵ=0.1
if rand < ϵ
    a = random
else
    a = argmax(q(s,a))

Decaying E-greedy (감쇠 E-greedy)

반복횟수가 많아질 수록 기존 E-greedy 보다 Exploration 기회가 많아지는 방식

# ϵ=0.1
for i in ragne(1000)
    ϵ=0.1/(i+1) # 반복될 수록 감쇠
    if rand < ϵ
        a = random
    else
        a = argmax(q(s,a))

try 수가 많아질 수록 Exploit < Exploration 로 변하게 된다.

Discount Factor (감쇠율)

위와 같은 길찾기 알고리즘에선 많은 길을 탐색할 수록 손해이다.
따라서 감쇠율을 지정해주는데

$\hat{q}*(s,a) \larr r+\gamma\max{a’}\hat{q}⁡_*(s’,a’)$

$\gamma=0.9$ 라고 한다면 아래 그림처럼 Optimal Action Value 가 설정된다.

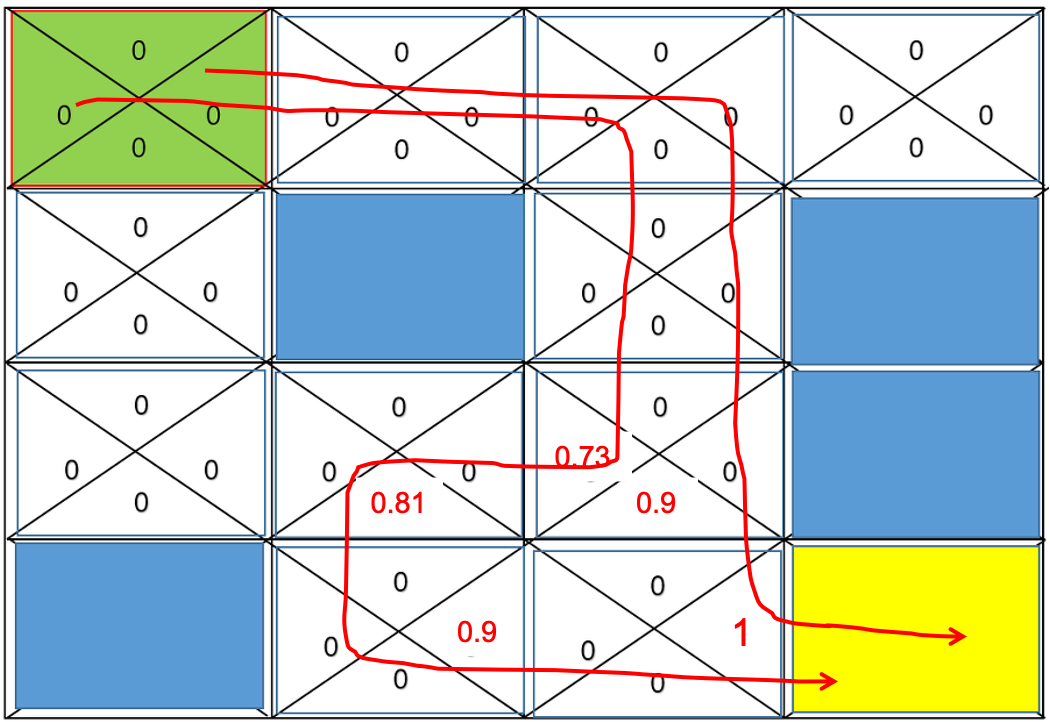
Stochastic Environment (확률적 환경)

Stochastic: 확률적인

위 예제는 State 에 대한 Reward 가 명확했지만
그렇지 않은경우도 있다.

예를들어 F 를 밝게되면 미끌어지는 확률이 추가되어, 미끄러져서 3칸을 강제이동 된다면

같은 행위를 해도 확률에 다라 Reward 가 달라질 수 있다면 Optimal Action Value 를 어떻게 구할 것인가

Law of Large Numbers(큰 수의 법칙: 여러번 반복 수행해서 같은 값을 반환하는 쪽으로 기우는 방식) 방법을 사용하면 된다.

Monte Carlo Simulation (MC Simulation)

s: Episode a: Action G: Return Reward Q: Action Value

위 그림과 같이 에피소드별 Return Value 를 테이블로 정의했을 때
강 상황마다 Action Value 가 업데이트 된다.

Action Value Function 으로 Reward 에 해당하는 G(goal) 값의 평균값을 사용하는 방식으로 수식을 나타내면 아래와 같다.

\[\mu_n = \frac{1}{n}[\sum^n_{i=1} x_i]\]

$\mu$ 기호를 사용해 평균(mean or expactation) 을 나타낸다.
수식을 조금더 확장하면 조금 더 수월한 공식(Incremental Mean: 증분평균)으로 표현할 수 있다.
$\begin{aligned} \mu_n &= \frac{1}{n}(\sum^n_{i=1} x_i) \\ &= \frac{1}{n}(x_n + \sum^{n-1}_{i=1} x_i) \\ &= \frac{1}{n}(x_n + (n-1)\mu_{n-1}) \\ &= \mu_{n-1} +\frac{1}{n}(x_n + \mu_{n-1}) \\ \end{aligned}$

Monte Carlo Simulation 의 문제점이 몇가지 있다.

에피소드가 늘어날수록 $\frac{1}{n}$ 에서 n 값이 0에 가까워지기 때문에 학습 속도가 줄어든다는 문제점이 발생한다.

그래서 총합 x 학습률로 Action Value 을 구성하기도 한다.
$Q_n \larr Q_{n-1} + \alpha(G_n - Q_{n-1})$

그리고 에피소드가 늘어나면 많은 연산이 필요하게 된다.
위의 경우 에피소드의 수가 36 에 선택 가능한 액션이 1개이지만
에피소드의 수, 액션의 수가 늘어나면 계산량도 급격히 많아진다.

또한 마리오게임과 같이 연속된 액션이 계속 이어지는 Continuous task 에도 Monte Carlo Simulation 방식을 사용하지 못한다.

Action Value 가 Incremental Mean 로 구해질 뿐 Q Function 은 기존 MDP 의 Q Function 과 같다.

\[\begin{aligned} q_\pi(s,a) &= E_\pi[G_t|S_t=s, A_t=a] \\ &= E_\pi[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1})|S_t=s, A_t=a] \end{aligned}\]

Temporal Difference Methods(TD Method)

Continuous task 에서 Monte Carlo Simulation 를 사용하지 못함으로 만들어진 방법
time step 마다 Action Value Function 을 업데이트한다.

Action Value Function 은 MC 방식과 비슷하다.
$Q_n=Q_{n-1} + \alpha(G_n - Q_{n-1})$

\[\begin{aligned} q(S_t,A_t) &\larr q(S_t,A_t) + \alpha(R_{t+1} + \gamma q(S_{t+1}, A_{t+1})-q(S_t,A_t)) \\ &= (1-\alpha)q(S_t,A_t) + \alpha(R_{t+1}+\gamma q(S_{t+1},A_{t+1})) \end{aligned}\]

Deep Q Learning

지금까지 Q Function 을 구하기 위해 어떤 방식이 되었건 상태별 Action 선택시 최적의 Action Value 를 저장해둔 행렬을 사용하였다.

문제는 위와 같이 너무 많은 state 를 가질때 터무니 없는 용량의 Matrix 를 가져야 한다는 것.
(maze 는 각 픽셀위치에 따른 상하좌우 action, video game 의 경우 80x80 픽셀에서 표현 가능한 모든 이미지 수)

이와 같은 상황에서 Action Value 를 예측 하기위해 Nueral Network 를 사용한다.

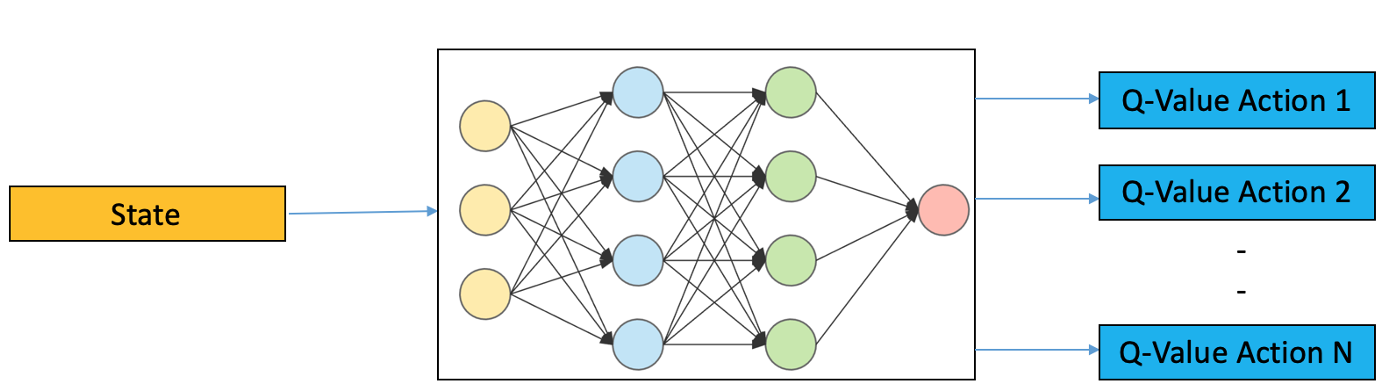
input 으로 state, output 의로 q-value 가 나온다.

$\gamma$ : discount factor, between(0, 1) $r$ : reward $a$ : current action $s$ : current state $a’$ : action after time t $a’$ : state after time t